风控建模流程

Posted 2023-05-03

参考技术A         以下以申请评分卡(A卡)建模为例，描述模型开发的基本流程：
1.数据准备：定义目标变量，整合样本特征；划分数据集：训练集、验证集与测试集，由于金融业务中的样本的积累周期比较长，因此测试集有必要划分为两种，一种为训练集时间跨度内，一种为训练集时间跨度之外，用时间外的测试集验证模型特征的稳定性。
2.探索性数据分析：统计每个特征取值的分布；统计每个特征的覆盖率，去掉覆盖率较低的特征；处理样本的异常值和缺失值。
3.数据预处理：根据经验对特征作预筛选，筛除于目标变量无关的特征；特征分箱；WOE转换。
4.特征选择：计算IV值，特征选择。
5.模型开发：常用逻辑回归模型进行拟合。
6.模型评估：模型常见的评估指标有AUC,ROC,KS,Gani-chat,Lift-chat，特征稳定性的评估指标psi。
7.生成评分卡。
流程示意图如下所示：

        不同的评分模型需要的数据是不同的，在建模之前需要对对要解决的问题建立明确的数学定义。
1.排除一些特定的建模用户
        用于建模的用户必须是日常审批中接触到的用户，不能是异常情况，比如欺诈等。
2.明确用户的属性
        用户的基本属性，比如学历、年龄、收入情况等；征信机构的数据和其他外部数据，比如芝麻分。
3.目标变量的确立
        评分模型是利用历史的数据预测未来的行为，需要明确定义正负样本的标签。不能出现歧义，重叠等。
4.划分数据集
        通常训练模型需要划分训练集、验证集与测试集。信贷业务中样本成熟的经历的时间比较长，因此测试集需要时间内和时间外的数据，时间内外是相对训练集的时间跨度而言，避免经过一段时间后特征波动或失效的发生。

EDA的实施主要包括：
1.描述性统计
        描述性统计是用一些统计量来对变量分析，如：平均值，标准差，最小值，最大值等。
2.统计每个变量值的分布、特征覆盖率及检验正态分布
        通常使用直方图绘制变量不同取值的样本分布，以及变量在样本中的覆盖率，筛除样本中有值特别少的变量。
3.极值的识别与处理
        每个变量需要设定一个正常的取值范围。对数量较少的超出正常范围的极端值作替换处理，若极端值的数量超过10%,则说明数据的生成机制不止一个。
4.缺失值的处理
4.1缺失值机制

1.特征初筛
        根据业务经验预先筛除掉与目标变量无关的变量。
2.特征分箱
1)对于连续变量可以使用等频分箱、等距分箱、卡方分箱与最优分箱；
2)对于离散变量，可以卡方分箱，对离散变量取值合并分箱。
3.特征编码
1)特征分箱离散化后可计算每个bin的woe值，形成每个bin的woe编码
2)one-hot编码
3)dummy编码，与one-hot编码类似

1.计算IV值与psi值
        IV(Information Value):信息价值。IV可以用来衡量自变量的预测能力；WOE(Weight of Evidence,证据权重)和IV使用来衡量变量的预测能力，值越大，表示此变量的预测能力越强。PSI可以用来衡量特征的稳定性。
        在训练模型时，挑选特征是一个比较复杂的过程，要考虑的因素有很多，比如，变量的预测能力，变量之间的相关性，变量的简单性(容易生成和使用)，变量的强壮性(不容易被绕过)，变量在业务中的可解释性。其中变量的预测能力可以通过IV值衡量。IV的计算是以WOE为基础的。

        要对一个变量进行WOE编码，必须对变量离散化(分箱)，分箱后，第i组的woe值得计算公式为:

其中， 为这个组中响应客户(风险模型中为违约客户，正样本)的，占总体正样本的比例， 为负样本所占比例， 为该分组中正样本数量， 为该组负样本数量， 代表总体样本中的正负样本数量，WOE实际代表该分组中的正负样本比例的差异，值越大，差异越大，该分组越能区分正负样本。第i组的IV 值为:

整个变量的IV值为(n个分组 值得嘉和)：

2.特征筛选
选择IV值高，PSI值低，覆盖率高的特征入模。

1.模型拟合
常用lr逻辑回归模型进行分类。
2.step-wise模型优化
根据p值筛选模型变量，原假设(变量不重要，与目标变量无光)，在此假设基础上计算chi-square,若chi-square值大，则p值小，p值<0.01说明变量很重要。

        模型拟合之后，需要评估模型的好坏。好的模型一般要有以下三个基本要求：
1.精确性。模型在预测时，要有一定的精确性；2.稳健性。模型必须对从总体样本中抽取的所有样本都有效；3.有意义
以下介绍几个常用的评价指标：
1.混淆矩阵
2.KS曲线
3.AUC曲线
4.ROC指标
5.Gini系数
6.Lift-chart提升图

        一个事件发生的几率（Odds），是指该事件发生的概率与该事件不发生概率的比值。若一个客户违约概率为p，则其正常的概率为1-p，由此可得：

此时，客户违约的概率p可以表示为:

评分卡表达式为：

其中A、B为常数。由于log函数在(0→+∞)单调递增，所以当用户违约几率Odds越大时，Score评分越低。通过给定 :
（1）某特定Odds时的Score值S0；
（2）该特定Odds值翻倍时Score增加值PD0;
通过给定值S0与PD0带入评分卡表达式，可求得A、B。

(未完待续。。。)

风控模型—WOE与IV指标的深入理解应用

风控业务背景

在评分卡建模流程中，WOE（Weight of Evidence）常用于特征变换，IV（Information Value）则用来衡量特征的预测能力。风控建模同学可能都很熟悉这两者的应用，但我们仍然可能疑惑诸如“如何调整WOE分箱？“、“WOE与LR之间的关系？”这些问题。

很多文章都已经讨论过这一命题，本文吸取归纳了前人的优秀成果，以期对WOE和IV给出一套相对完整的理论解释。主要创新点在于：

1. 用图表可视化展示WOE和IV指标的计算过程和业务含义，适用于快速入门实践的读者。

2. 从信息论、贝叶斯理论角度来阐述其中蕴含的数学原理，适用于希望加深理解的读者。

目录

Part 1. WOE和IV的应用价值

Part 2. WOE和IV的计算步骤

Part 3. WOE定义的初步猜想

Part 4. 从贝叶斯角度理解WOE

Part 5. WOE与评分卡的渊源

Part 6. 从相对熵角度理解IV

致谢

版权声明

参考资料

Part 1. WOE和IV的应用价值

WOE（Weight of Evidence）叫做证据权重，大家可以思考下为什么会取这个名字？

那么WOE在业务中常有哪些应用呢？

1.  处理缺失值：当数据源没有100%覆盖时，那就会存在缺失值，此时可以把null单独作为一个分箱。这点在分数据源建模时非常有用，可以有效将覆盖率哪怕只有20%的数据源利用起来。

2. 处理异常值：当数据中存在离群点时，可以把其通过分箱离散化处理，从而提高变量的鲁棒性（抗干扰能力）。例如，age若出现200这种异常值，可分入“age > 60”这个分箱里，排除影响。

3.  业务解释性：我们习惯于线性判断变量的作用，当x越来越大，y就越来越大。但实际x与y之间经常存在着非线性关系，此时可经过WOE变换。

IV（Information Value）是与WOE密切相关的一个指标，常用来评估变量的预测能力。因而可用来快速筛选变量。在应用实践中，其评价标准如下：

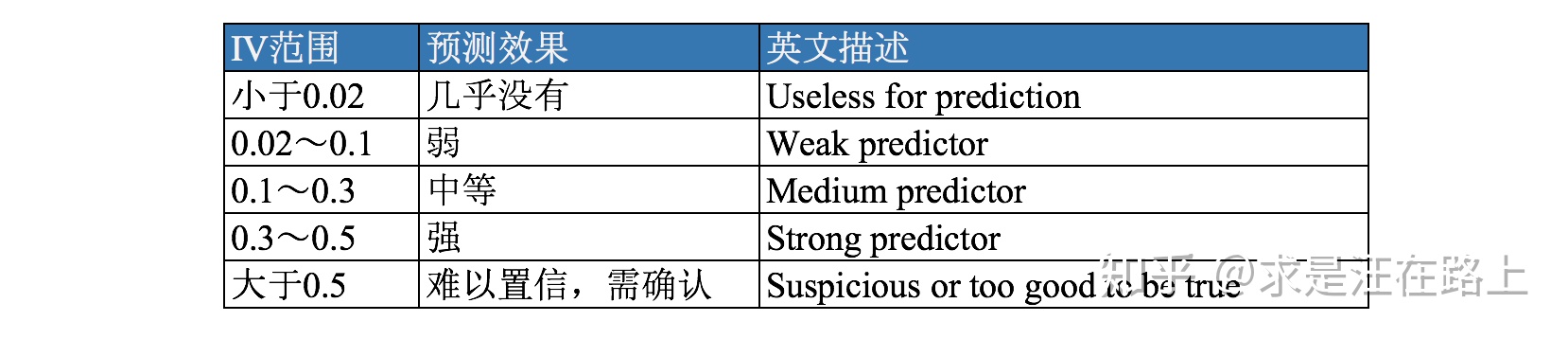
在此引用一段话来说明两者的区别和联系：

1. WOE describes the relationship between a predictive variable and a binary target variable.

2. IV measures the strength of that relationship.

Part 2. WOE和IV的计算步骤

在定性认识到WOE和IV的应用价值后，我们就慢慢揭开其面纱，从理性角度进行分析。通常其公式定义如下：

而IV的计算公式定义如下，其可认为是WOE的加权和。为什么会定义成这样？

为帮助大家理解，现以具体数据介绍WOE和IV的计算步骤，如图1所示。

• step 1. 对于连续型变量，进行分箱（binning），可以选择等频、等距，或者自定义间隔；对于离散型变量，如果分箱太多，则进行分箱合并。

• step 2. 统计每个分箱里的好人数(bin_goods)和坏人数(bin_bads)。

• step 3. 分别除以总的好人数(total_goods)和坏人数(total_bads)，得到每个分箱内的边际好人占比(margin_good_rate)和边际坏人占比(margin_bad_rate)。

• step 4. 计算每个分箱里的

• step 5. 检查每个分箱（除null分箱外）里woe值是否满足单调性，若不满足，返回step1。注意⚠️：null分箱由于有明确的业务解释，因此不需要考虑满足单调性。

• step 6. 计算每个分箱里的IV，最终求和，即得到最终的IV。

  备注：好人 = 正常用户，坏人 = 逾期用户

图 1 - WOE和IV计算

另外还需要注意什么呢？

1. 分箱时需要注意样本量充足，保证统计意义。

2.  若相邻分箱的WOE值相同，则将其合并为一个分箱。

3. 当一个分箱内只有好人或坏人时，可对WOE公式进行修正如下：

在实践中，我们还需跨数据集检验WOE分箱的单调性。如果在训练集上保持单调，但在验证集和测试集上发生翻转而不单调，那么说明分箱并不合理，需要再次调整。下图是合理的WOE曲线变化示例。

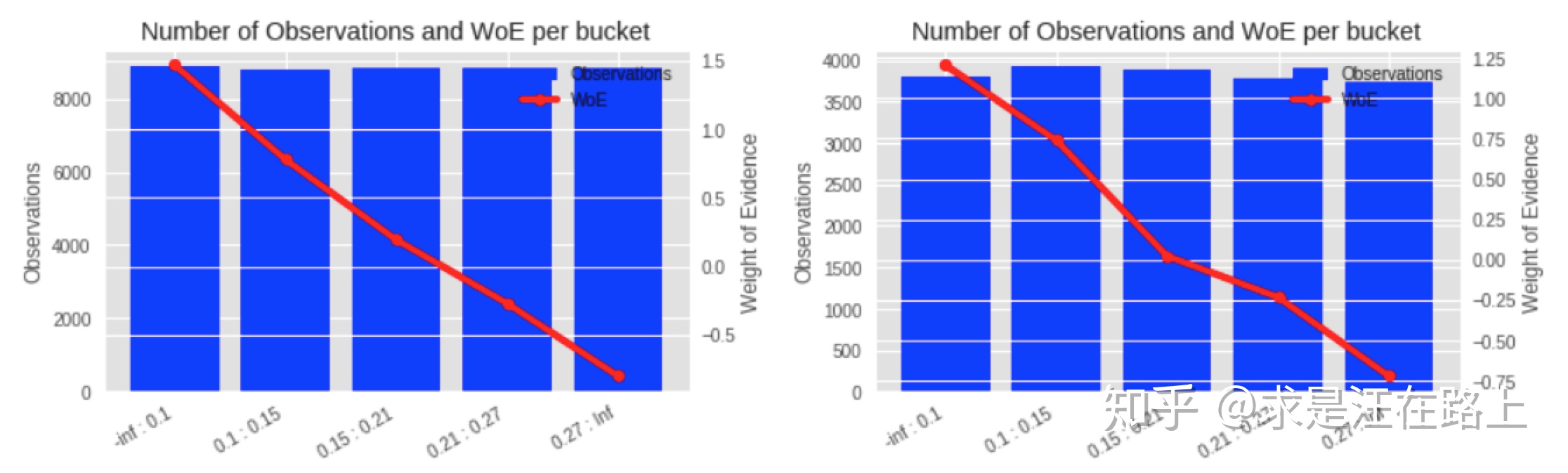
图 2 - 左为训练集WOE曲线，右为测试集WOE曲线（都单调）

这里提前给大家留下问题：为什么要保持WOE曲线要保持单调性？在某些情况下是不是可以不满足单调性？是不是线性就更好？WOE曲线的斜率是否越陡越好？

Part 3. WOE定义的初步猜想

为了搞清楚为什么WOE公式是如此定义的，我们尝试对其进行各种变换。

WOE = ln (第i个分箱的坏人数 / 总坏人数) - ln (第i个分箱的好人数 / 总好人数)

此时可以理解为：每个分箱里的坏人分布相对于好人分布之间的差异性。

我们对公式再变换为：

WOE = ln (第i个分箱的坏人数 / 第i个分箱的好人数) - ln (总坏人数 / 总好人数)

此时可以理解为：每个分箱里的坏好比(Odds)相对于总体的坏好比之间的差异性。

但是，为什么要再套一个对数ln？

之前看到一种解释是为了进行平滑处理。那么为什么不引入拉普拉斯平滑，也就是在分子分母中都加上一个数？如果加上1，那么公式推导如下：

此时含义是：总体good_rate相对于分箱内good_rate的倍数。

其实发现这种形式会更符合我们的直觉。因此，“取对数是为了平滑处理”——这种解释无法说服我们。

同时，我们又会疑惑为什么不把WOE定义为：

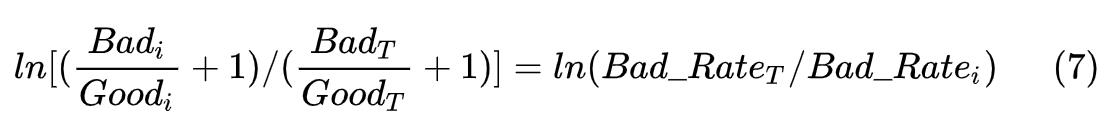
 因此，我们发现无法通过常规思维去理解这一切，于是开始去寻找新的工具。

Part 4. 从贝叶斯角度理解WOE

贝叶斯理论认为我们认知世界是一个循序渐进的过程，首先我们有一个主观的先验认知，进而不断通过观测数据来修正先验认知，得到后验认知。随着这个过程不断迭代，我们对世界的认识也就越来越完善。其中，从观测数据中提取信息来支撑我们的原始假设就是WOE。

在信贷风控中，识别好人和坏人也是同样的道理。我们根据历史样本数据形成一个先验认知：

当Odds小于1时，预测为Good的概率更高，此时我们认为一般情况下都是好人。但实际中样本会受到各种因素（自变量）影响而导致变坏。

因此，我们就开始搜集样本的各种特征，希望这些证据能帮助我们对这个样本全貌有更为全面的理解，进而修正我们的先验认识。这个过程用公式可以表达如下。提示：留意两侧为什么会取自然对数ln，而不是log？

其中， 表示后验项； 表示根据观测数据更新信息，即WOE； 表示先验项。

如果搜集到的数据与先验认知的差距不大，我们就认为这个数据中得到的证据价值不大，反之则认为带来的信息越多。因此，WOE用以衡量对先验认识修正的增量，这就是WOE被取名为“证据权重”的原因。

Part 5. WOE与评分卡模型的渊源

评分卡模型基于假设“历史样本和未来样本服从同一总体分布”，故而才能从历史样本中归纳出数理统计规律来预测未来样本的表现。评分卡通常采用逻辑回归（Logistics Regression）进行建模，其原因有很多，比如可解释性、简单模型、小样本学习等等。

我们从“数据->信息->知识->决策”框架来解释完整的流程。

• step1. 从不同信道里获取了观测数据（Data），并从中提取了特征X。

• step2. 此时发现各渠道采集的信息并不在一个尺度上，无法融合。因此，我们通过WOE变换对信息进行处理，将其对标到统一尺度上。

• step3. LR模型对不同信息采用不同权重(weight)进行加权融合，并通过sigmoid函数映射为0～1的概率。

• step4. 基于LR模型的输出结果，人工进行决策，判定好人还是坏人。

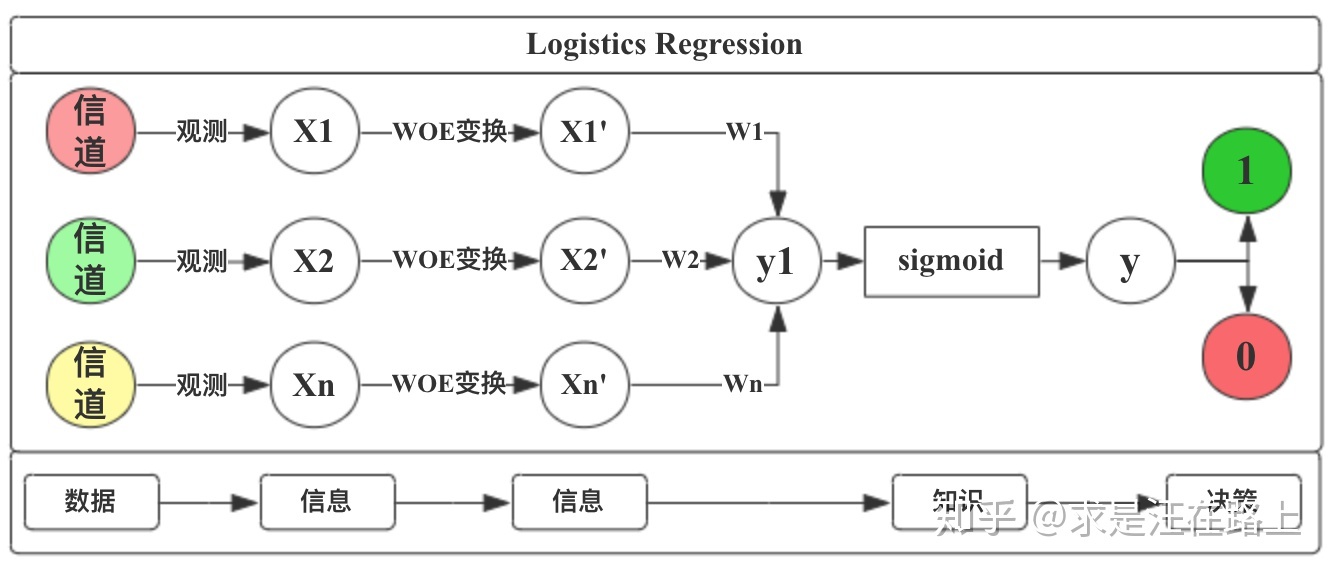
图 3 - LR模型

初识WOE是在评分卡模型中，当时仍不懂它们之间的关系。我们可能会疑惑，WOE是在建立评分卡理论时应运而生，还是属于一种通用的信息变换方法？

为了简化处理，我们只考虑一个自变量 ，那么评分卡模型的形式为：

我们可以观察到WOE公式与LR左边部分是如此相似。回到贝叶斯角度解释WOE时留下的提示——两侧为什么会取自然对数ln，而不是log？

在评分卡模型中我们就得到了一种可能的解释，主要是为了适配于LR模型。

接下来解释WOE曲线需要保持单调性的意义。

首先，引入Odds（几率）概念：

Odds=P/(1-P)，P为预测为1的概率。Odds越大，代表预测为1的概率越高。

 然后我们把相邻两个分箱的WOE值相减。

在上述等式中，权重w可以认为是常数，因此我们会发现：

1. 分子和分母的变化趋势一致，当WOE单调递增时，分子中ln(odds)也是单调变化，由此P(Y=Bad)也是单调变化。

2. 当分母变化越大时，分子也会变化越大，宏观表现就是WOE曲线越陡。此时，好人与坏人的区分将会越明显。

Part 6. 从相对熵角度理解IV

在《稳定性评估指标深入理解应用》一文里，我们从相对熵（KL散度）角度理解了PSI的数学原理。

我们会留意到下面三者好像都和“信息”有关系，那这三者之间存在怎样的联系呢？

信息熵（Shannon entropy）、相对熵（relative entropy）、 信息量（Information Value）

因此，我们把PSI、IV的计算公式放在一起进行对比，希望能观察出一些线索。

我们会发现两者形式上是完全一致的，这主要是因为它们背后的支撑理论都是相对熵。我们可以归纳为：

1. PSI衡量预期分布和实际分布之间的差异性，IV把这两个分布具体化为好人分布和坏人分布。IV指标是在从信息熵上比较好人分布和坏人分布之间的差异性。

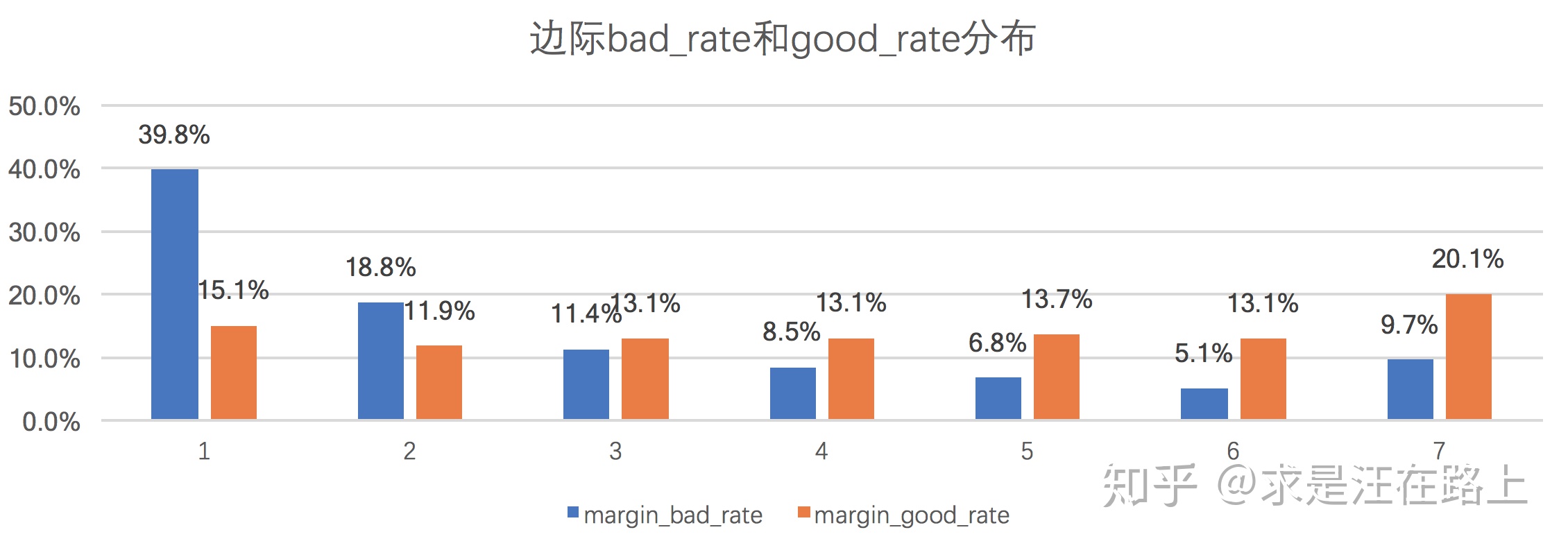
图 4 - 好人与坏人分布对比

2. PSI和IV在取值范围与业务含义的对应上也是存在统一性，只是应用场景不同——PSI用以判断变量稳定性，IV用以判断变量预测能力。

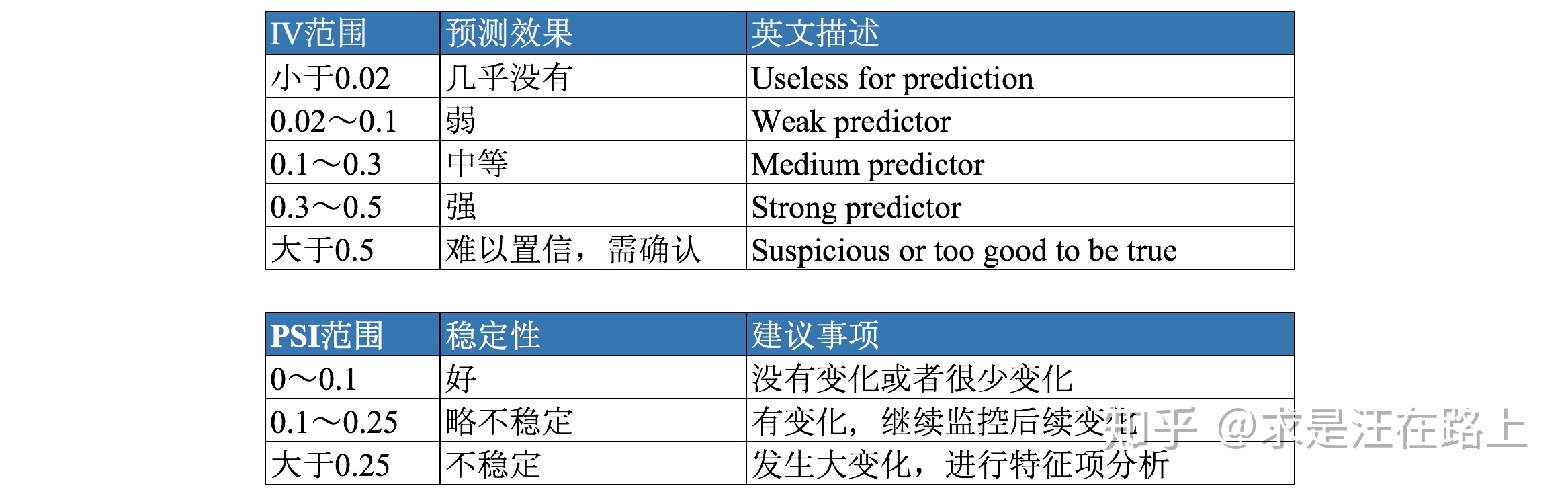
图 5 - PSI和iV指标的含义对比

致谢

所有参考资料中的各位作者，感谢给我的启发。文中仍有理解不到位之处，在此抛砖引玉。