HDU--1754 区间最值(树状数组做法)

Posted 2021-02-19 liyexin

地址：http://acm.hdu.edu.cn/showproblem.php?pid=1754

 

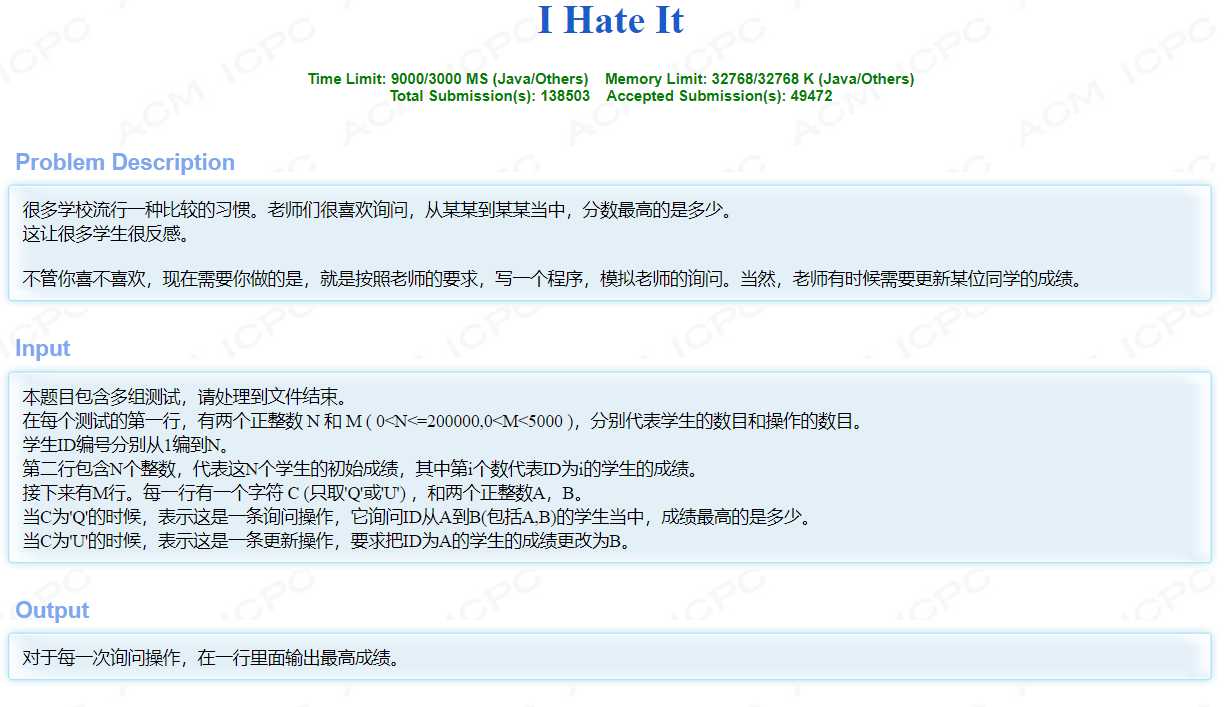
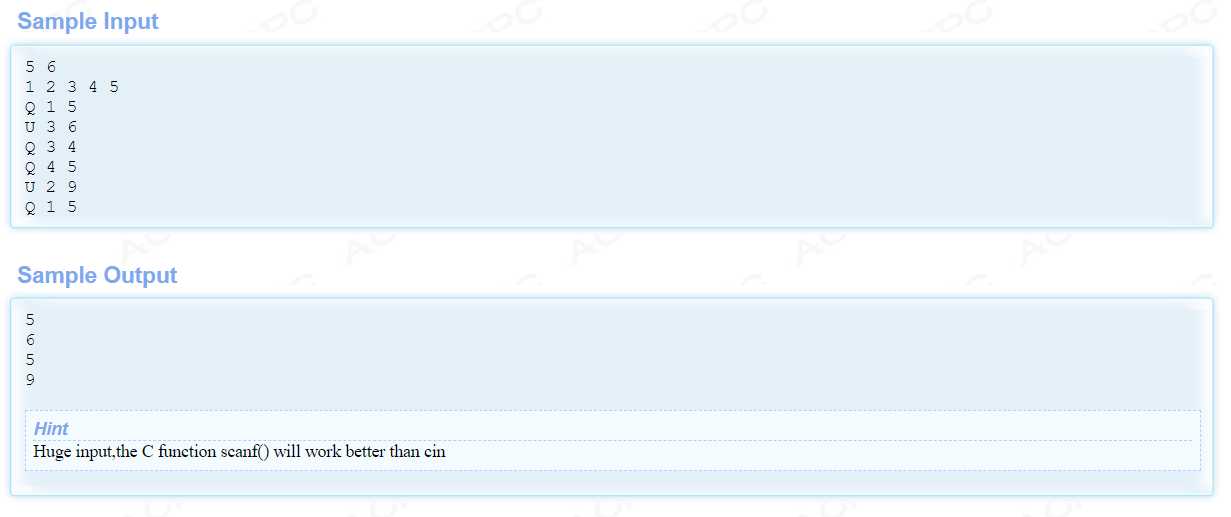
 　　　　解析：先说update操作。c[]表示所管辖的区间范围里的最大值。

void update(int id,int x)
{
    while(id<=n)
    {
        c[id]=x;
        for(int i=1;i<lowbit(id);i+=lowbit(i))
        {
            c[id]=max(c[id],c[id-i]);
        }
        id+=lowbit(id);
    }
}

　　　　由于加入了一个新值，所以直接改变c[]是没有问题的。看这个for。举个例子：id=8，i=1，2，4。c[8]分别和c[4],c[6]c[7]进行了max更新，所以这个 id-i，是把所有id以内的区间进行了更新，覆盖了所有i<=id的数，很巧妙~。这个例子看这个图更是一目了然了：

 

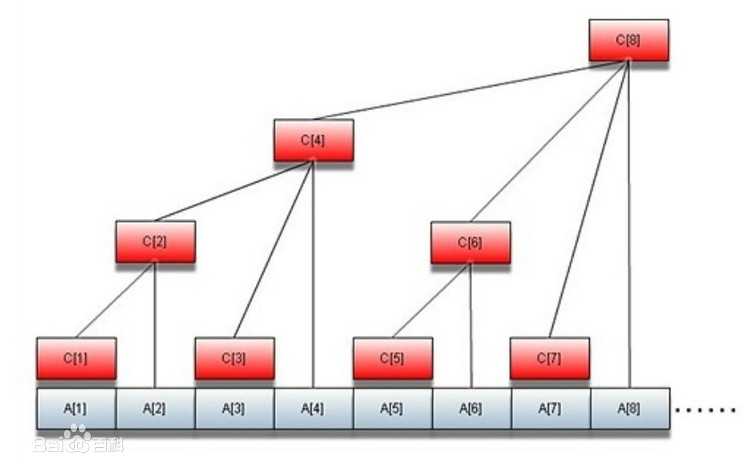
　　　　接下来是query操作：

 

int query(int l,int r)
{
    int md=0;
    while(l<=r)
    {
        md=max(md,a[r]);
        r--;
        for(;r-l>=lowbit(r);r-=lowbit(r))
        {
            md=max(md,c[r]);
        }
    }
    return md;
}

 

　　　　对于r来讲，它所管辖的有lowbit(r)个区间。所以对于[l,r]如果r-l>=lowbit(r)，那么c[r]可以直接拿来用。而如果lowbit(r)超出了[l,r]，那么就r--对L进行逼近。

　　　 Ac代码：

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
typedef long long ll;
const int maxn=2e5+10;
int c[maxn],a[maxn],n,m;
int lowbit(int x)
{
    return x&(-x);
}
void update(int id,int x)
{
    while(id<=n)
    {
        c[id]=x;
        for(int i=1;i<lowbit(id);i+=lowbit(i))
        {
            c[id]=max(c[id],c[id-i]);
        }
        id+=lowbit(id);
    }
}
int query(int l,int r)
{
    int md=0;
    while(l<=r)
    {
        md=max(md,a[r]);
        r--;
        for(;r-l>=lowbit(r);r-=lowbit(r))
        {
            md=max(md,c[r]);
        }
    }
    return md;
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=1;i<=n;i++)
            c[i]=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            update(i,a[i]);
        }
        char ch[12];
        while(m--)
        {
            scanf("%s",ch);
            if(ch[0]==‘Q‘)
            {
                int l,r;
                scanf("%d%d",&l,&r);
                cout<<query(l,r)<<endl;
            }
            else
            {
                int id,x;
                scanf("%d%d",&id,&x);
                a[id]=x;
                update(id,x);
            }
        }
    }
}