图总结

Posted 2021-02-19 0695x

一、思维导图

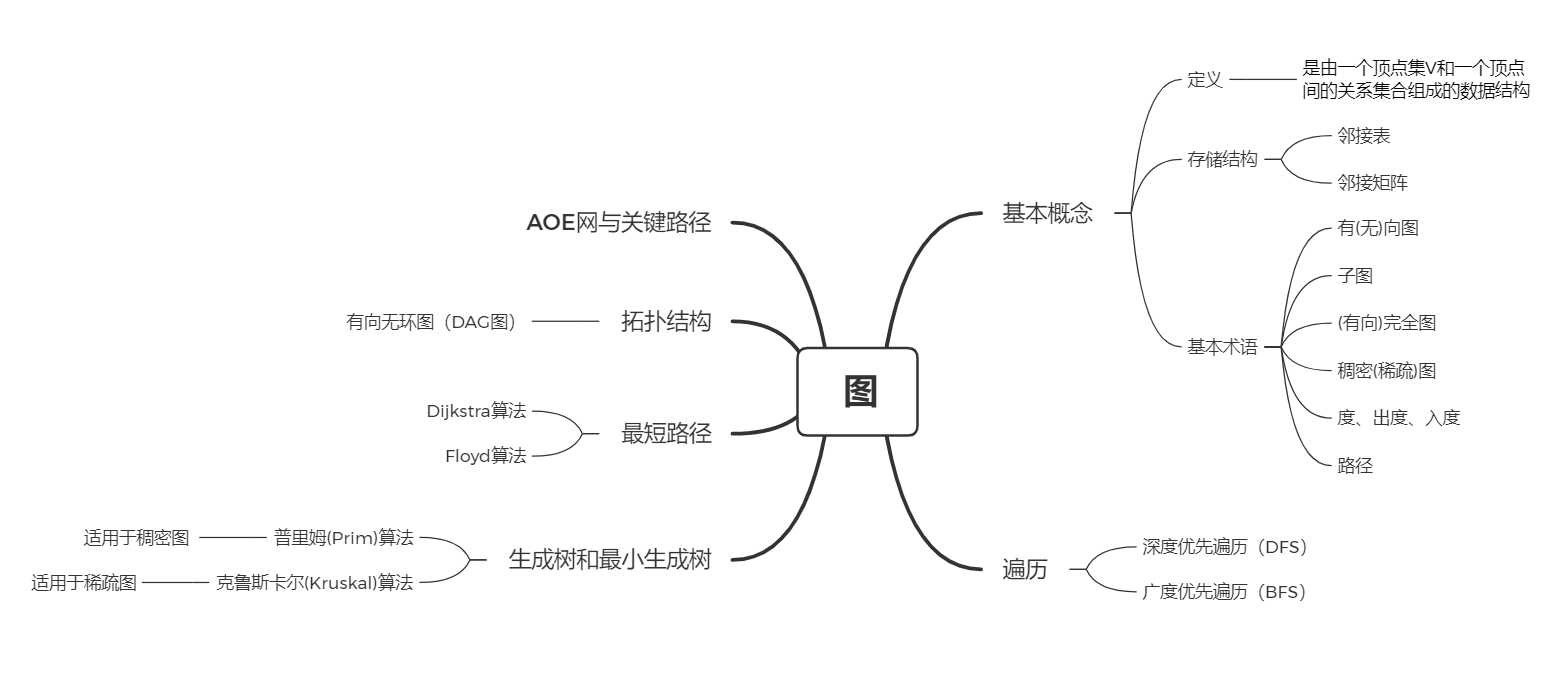
二、重要概念

1.DFS

时间复杂度为O(n+e)。

2.BFS

时间复杂度为O(n+e)。

3.最小生成树

1）Prim算法

时间复杂度为O(n*n)，所以更适用于稠密图。

2） Kruskal算法

时间复杂度为O(elog2e)，所以更适用于稀疏图。

4.最短路径

1） Dijkstra算法

特点：每次以一个顶点源点，重复执行Dijkstra算法n次。时间复杂度为O(n^3)。

2）Floyd算法

时间复杂度也为O(n^3)。

5.拓扑排序

前提：图为有向无环图，即图为简单路径。

6.关键路径

整个工程完成的时间：从有向图的源点到汇点的最长路径。

三、疑难问题及解决方案

如何解决Floyd算法？

第一、先找出最短的距离
第二、然后在考虑如何找出对应的行进路线。
如何找出最短路径呢，这里还是用到动态规划的知识，对于任何一个城市而言，i到j的最短距离不外乎存在经过i与j之间经过k和不经过k两种可能，所以可以令k=1，2，3，...，n(n是城市的数目)，在检查d(ij)与d(ik)+d(kj)的值；在此d(ik)与d(kj)分别是目前为止所知道的i到k与k到j的最短距离，因此d(ik)+d(kj)就是i到j经过k的最短距离。所以，若有d(ij)>d(ik)+d(kj)，就表示从i出发经过k再到j的距离要比原来的i到j距离短，自然把i到j的d(ij)重写为d(ik)+d(kj)，每当一个k查完了，d(ij)就是目前的i到j的最短距离。重复这一过程，最后当查完所有的k时，d(ij)里面存放的就是i到j之间的最短距离了。

网上找到的解决Floyd算法： https://www.cnblogs.com/wangyuliang/p/9216365.html