matlab第六章数据分析与多项式计算

Posted 2021-02-18 bujilangzi

MATLAB练习

第六章数据分析与多项式计算

1、max和min

1、分别求矩阵A中各列和各行元素中的最大值。max和min的用法一样
 % 【例6.1】分别求矩阵中各列和各行元素中的最大值。

A=[54,86,453,45;90,32,64,54;-23,12,71,18];
y1=max(A);   %求矩阵A中各列元素的最大值
y2=max(A,[],2)   %求矩阵A中各行元素的最大值
?
y2 =
?
   453
    90
    71
?
>> y1
?
y1 =
?
    90    86   453    54    

    
2、求矩阵X、Y所有同一位置上的较大元素构成的新矩阵p。

>> X=[443,45,43;67,34,-43];
>> Y=[65,73,34;61,84,326];
>> p=max(X,Y);%两矩阵元素的同一位置比较，返回最大值
p =
   443    45    45
    67    45    45

　　

3、将矩阵A的元素与常数x比较，返回较大的元素，构成同A阶数相同的矩阵，元素取

>> x=45;
>> p=max(A,x);
p =
   443    45    45
    67    45    45

　　

2、求和sum(A)和sum(X,dim)、求积prod用发同sum

求矩阵A的每行元素之和和全部元素之和。
>> A=[9,10,11,12;100,200,300,400;50,60,50,60];
>> S=sum(A,2)   %求A每行元素的和 
S =
          42
        1000
         220
>> p=sum(A)   %求A的全部元素之和
P =
   1262

　　

?

3、求平均值和中值

求平均数格式：
M=mean(X);    X:向量或者矩阵 
M=mean(A,dim);  dim=1或2(行)
求中值格式：
M=median(X);    X:向量或者矩阵 
M=median(A,dim);  dim=1或2(列)

例如，求向量x = [-8，2，4，7，9]与y = [-8，2，4，7，9，15]的平均值和中值。

>> x=[-8,2,4,7,9];            % 奇数个元素
>> mx=[mean(x),median(x)]
mx =
    2.8000    4.0000
>> y=[-8,2,4,7,9,15];           % 偶数个元素
>> my=[mean(y), median(y)]
my =
    4.8333    5.5000

　　

4、求累加和与累乘积

累加格式：
B = cumsum(X)；      X：向量或矩阵
B = cumsum(X,dim)：  dim：1或2(列)
累乘积用法同累加和
B = cumprod(X)；      X：向量或矩阵
B = cumprod(X,dim)：  dim：1或2(列)
列【例6.4】求S=1+（1+2）+(1+2+3)+…+(1+2+…+10)的值。

>> y=cumsum(1:10)
y =
     1     3     6    10    15    21    28    36    45    55
>> s=sum(y)
s =
   220

　　

5、统计描述函数

1、标准差

调用格式
s = std(X , w, dim)   X矩阵或者行向量，w：用于指定标准差的计算方法；w=0或1  dim=1或2(求行元素标准差)
某次射击选拔比赛中小明与小华的10次射击成绩（单位：环）如表6.1所示，试比较两人的成绩。
小明：7,4,9,8,10,7,8,7,8,7
小华：7,6,10,5,9,8,10,9,5,6

>> hitmark=[7,4,9,8,10,7,8,7,8,7;7,6,10,5,9,8,10,9,5,6];
>> mean(hitmark,2)；    %按行求平均值，返回一个列向量
ans =
    7.5000
    7.5000
>> std(hitmark,[],2)；按行求标准差，返回一个列向量
ans =
    1.5811
    1.9579

　注意：标准差越小，成绩波动越小

2、方差

var函数的调用格式为
V = var(X, w, dim)    x：向量或者矩阵   w用于指定权重方案(为0:或为1)   dim=1(求各列方差)或2
?
考察一台机器的产品质量，判定机器工作是否正常。根据该行业通用法则：如果一个样本中的14个数据项的方差大于0.005，则该机器必须关闭待修。假设搜集的数据如表6.2所示，问此时的机器是否必须关闭？

>> samples=[3.43,3.45,3.43,3.48,3.52,3.50,3.39,3.48,3.41,3.38,3.49,3.45,3.51,3.50];
>>var_samples=var(samples);
var_samples =
    0.0021

3、相关系数

[R,P]=corrcoef(X,Y)：     %R：相关系数矩阵，p:p值矩阵      X和我Y：
矩阵返回相关系数矩阵和p值矩阵。如果得到的p值矩阵的非对角线元素小于显著性水平（即90%置信区间，默认为 0.05），则R中的相应相关性被视为显著
[R,P]=corrcoef(X)     
【例6.7】随机抽取15名健康成人，测定血液的凝血酶浓度及凝血时间，数据如表6.3所示。分析凝血酶浓度与凝血时间之间的相关性。

>> density=[1.1,1.2,1.0,0.9,1.2,1.1,0.9,0.6,1.0,0.9,1.1,0.9,1.1,1,0.7];  %凝血酶浓度
>> cruortime=[14,13,15,15,13,14,16,17,14,16,15,16,14,15,17];   %凝血时间
>> [R,P]=corrcosf(density,cruortime)
R =
    1.0000   -0.9265
   -0.9265    1.0000

注意;R的绝对值接近1，说明相关程度高

4、协方差

C = cov(x)：
C = cov(x,y)
随机抽取15名健康成人，测定血液的凝血酶浓度及凝血时间，数据如表6.3所示。分析凝血酶浓度与凝血时间之间的相关性

>> density=[1.1,1.2,1.0,0.9,1.2,1.1,0.9,0.6,1.0,0.9,1.1,0.9,1.1,1,0.7];
>> cruortime=[14,13,15,15,13,14,16,17,14,16,15,16,14,15,17];
>> C=cov(density,cruortime)
C =
    0.0289   -0.2014
   -0.2014    1.6381
?　

注意：如果两个变量的协方差是正值，说明两者是正相关的，即两个变量的变化趋势一致；如果协方差为负值，则说明两者是负相关的，即两个变量的变化趋势相反；如果协方差为0，说明两者之间没有关系
?

6排序

[Y,I]=sort(X, dim, mode)    Y是排序后的矩阵，而I记录Y中的元素在X中的位置，mode指明排序的方法，‘ascend‘（默认值）为升序，‘descend‘为降序
6.8】对二维矩阵A=[1,-8,5;4,12,6;13,7,-13];做各种排序

>> A=[1,-8,5;4,12,6;13,7,-13];
>> Y=sort(A,2,‘descend‘)            %对A的每行按降序排序
Y =
     5     1    -8
    12     6     4 
    13     7   -13
>> [X,I]=sort(A) %对A的每列按升序排序，矩阵I存储X各元素在A对应列中的行号
X =
     1    -8    -13
     4     7     5
    13    12     6
I =
     1     1     3
     2     3     1
     3     2     2

　　

?
?

6.2多项式计算

6.2.1多项式的四则运算

1、多项式的加减运算

计算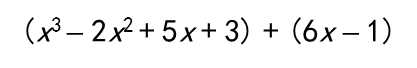

>> a=[1,-2,5,3];
>> b=[0,0,6,-1];
>> c=a+b
c =
     1    -2    11 

　　

2、多项式的乘除

w = conv(P1,P2)
[Q,r] = deconv(P1,P2)
P1、P2是两个多项式的系数向量
w是两个多项式相乘所得r
如果多项式
?

>> A=[1,8,0,0,-10];
>> B=[2,-1,3];
>> C=conv(A,B)
C =
     2    15    -5    24   -20    10   -30
>> [P,r]=deconv(A,B)
P =
        0.5000    4.2500    1.3750
r =
        0         0         0  -11.3750  -14.1250
以下命令验证deconv和conv是互逆的。
>> conv(B,P)+r
ans =
     1     8     0     0   -10

6.2.2多项式求导

k=polyder(P)：求多项式P的导数，即 
k=polyder(P,Q)：求P·Q的导数，即 
[q,d]=polyder(P,Q)：求P/Q的导数
?

>> P=[1];
>> Q=[1,0,5];
>> [p,q]=polyder(P,Q)
p =
    -2     0
q =
     1     0    10     0    25

　　

6.2.3多项式的求值

1、代数多项式求值

y = polyval(p,x)   p是多项式系数向量。  x：标量，向量，矩阵
?
【例6.11】已知多项式x4 + 8x3 - 10，分别取x = 1.2和一个2 × 4矩阵为自变量计算该多项式的值。
?

>> A=[1,8,0,0,-10];       % 4次多项式系数
>> x=1.2;                 % 取自变量为一数值
>> y1=polyval(A,x)
y1 =
    5.8976
>> x=randi(9,2,4) %randi(imax,m,n)函数：生成一组值在[1, imax]区间均匀分布的随机整数，构建m × n矩阵
x =
     8     2     6     3
     9     9     1     5
>> y2=polyval(A,x) % 分别计算矩阵x中各元素为自变量的多项式之值
y2 =
        8182          70        3014         287
       12383       12383          -1        1615?

?

2、矩阵多项式求值

polyval(P,A);   A.*A.*A-5*A.*A+8*ones(size(A))
?
polyvalm(P,A)  的含义为 A：方阵   A*A*A-5*A*A+8*eye(size(A))
?
?
以多项式x4 + 8x3 -10为例，取一个2 × 2矩阵为自变量分别用polyval和polyvalm计算该多项式的值。

>> A=[1,8,0,0,-10];             % 多项式系数
>> x=[-1,1.2; 2,-1.8];         % 给出一个矩阵x
>> y1=polyval(A,x)              % 计算代数多项式的值
y1 =
  -17.0000    5.8976
   70.0000  -46.1584
>> y2=polyvalm(A,x)             % 计算矩阵多项式的值
y2 =
  -60.5840   50.6496
   84.4160  -94.3504

　　

6.2.4多项式的求根

x=roots(P)    P为多项式的系数向量
?
【例6.13】已知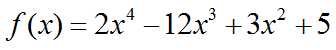

（1）计算f(x) = 0的全部根。
（2）由方程f(x) = 0的根构造一个多项式g(x)，并与f(x)进行对比。

?

>> P=[2,-12,3,0,5];
>> X=roots(P)            %求方程f(x)=0的根
X =
5.7246 + 0.0000i
0.8997 + 0.0000i          
  -0.3122 + 0.6229i
  -0.3122 - 0.6229i
>> G=poly(X)            %求多项式g(x)
G =
1.0000   -6.0000    1.5000   -0.0000    2.5000

　　

6.2.5多项式的除法变换

[r,p,k] = residue(b,a)
[b,a] = residue(r,p,k)   
a、b 分别为分式的分母多项式、分子多项式的系数向量，r是分数多项式的商式的系数向量，p为分数多项式的极点，k为分数多项式的余式的系数向量
【例6.14】已知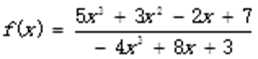

 

（1）将f(x)进行分式分解。
（2）由分解的分式合成g(x)，并与f(x)进行对比。

?

>> b = [5 3 2 7];                %分子系数
>> a = [-4 0 8 3];               %分母系数
>> [r, p, k] = residue(b,a)       %r分数多项式的商式系数向量
r =
   -1.4167
   -0.6653
    1.3320
p =                                 %p为分数多项式的极点
    1.5737
   -1.1644
   -0.4093
k =
   -1.2500
>> [b,a] = residue(r,p,k)
b =
   -1.2500   -0.7500    0.5000   -1.7500
a =
    1.0000   -0.0000   -2.0000   -0.7500

　　

6.3数据插值

6.3.1一维数据插值

vq = interp1(x,v,xq,method,extrapolation)
vq = interp1(x,v,xq,method,extrapolation)
x、v是两个等长的已知向量，分别存储采样点和采样值。若同一个采样点有多种采样值，则v可以为矩阵，v的每一列对应一种采样值。
输入参数xq存储插值点，输出参数vq是一个列的长度与xq相同、宽度与v相同的矩阵。
选项method用于指定插值方法,可取值如下。
    ‘linear’（默认值）：线性插值。
    ‘pchip’：分段3次埃尔米特插值
    ‘spline’：3次样条插值
    ‘ nearest’：最近邻点插值
    ‘next’：取最后一个采样点的值作为插值点的值
    ‘previous‘：取前一个采样点的值作为插值点的值
    标量：设置域外点的返回值
?
【例6.15】表6.4所示为我国0~6个月婴儿的体重、身长参考标准，用3次样条插值分别求得婴儿出生后半个月到5个半月每隔1个月的身长、体重参考值。

 

>> tp=0:1:6;    %采样点
>> bb=[50.6,3.27;56.5,4.97;59.6,5.95;62.3,6.73;64.6,7.32;65.9,7.70;68.1,8.22]; %采样值
>> interbp=0.5:1:5.5;   
>> interbv=interp1(tp,bb,interbp,‘spline‘)   %用3次样条插值计算
interbv =
   54.0847    4.2505
   58.2153    5.5095
   60.9541    6.3565
   63.5682    7.0558
   65.2981    7.5201
   66.7269    7.9149

　

 

 

 

 

 

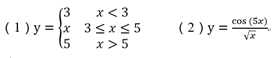
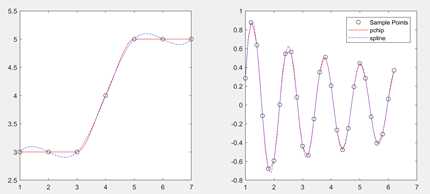
x1 = 1:7;    
subplot(1,2,1)
y1=x1;
y1(x1<3)=3;
y1(x1>5)=5;
xq1 = 1:0.1:7;   %存储插值点
p1 = interp1(x1,y1,xq1,‘pchip‘);   %分段3次埃尔米特插值
s1 = interp1(x1,y1,xq1,‘spline‘);    %3次样条插值
plot(x1,y1,‘ko‘,xq1,p1,‘r-‘,xq1,s1,‘b-.‘) subplot(1,2,2) x2 = 1:0.2:2*pi;    %‘ko‘:黑圆圈作为数据点标记
y2 = cos(5*x)./sqrt(x); xq2 = 1:0.1:2*pi;   
p2 = interp1(x2,y2,xq2,‘pchip‘);
s2 = interp1(x2,y2,xq2,‘spline‘); plot(x2,y2,‘ko‘,xq2,p2,‘r-‘,xq2,s2,‘b-.‘)； 
legend(‘Sample Points‘,‘pchip‘,‘spline‘)

 

 

 

6.3数据插值

6.3.1一维数据插值

vq = interp1(x,v,xq,method,extrapolation)
vq = interp1(x,v,xq,method,extrapolation)
x、v是两个等长的已知向量，分别存储采样点和采样值。若同一个采样点有多种采样值，则v可以为矩阵，v的每一列对应一种采样值。
输入参数xq存储插值点，输出参数vq是一个列的长度与xq相同、宽度与v相同的矩阵。
选项method用于指定插值方法,可取值如下。
    ‘linear’（默认值）：线性插值。
    ‘pchip’：分段3次埃尔米特插值
    ‘spline’：3次样条插值
    ‘ nearest’：最近邻点插值
    ‘next’：取最后一个采样点的值作为插值点的值
    ‘previous‘：取前一个采样点的值作为插值点的值
    标量：设置域外点的返回值
?
【例6.15】表6.4所示为我国0~6个月婴儿的体重、身长参考标准，用3次样条插值分别求得婴儿出生后半个月到5个半月每隔1个月的身长、体重参考值。

 

 

 

>> tp=0:1:6;    %采样点
>> bb=[50.6,3.27;56.5,4.97;59.6,5.95;62.3,6.73;64.6,7.32;65.9,7.70;68.1,8.22]; %采样值
>> interbp=0.5:1:5.5;   %8存储插入点
>> interbv=interp1(tp,bb,interbp,‘spline‘)   %用3次样条插值计算
interbv =
   54.0847    4.2505
   58.2153    5.5095
   60.9541    6.3565
   63.5682    7.0558
   65.2981    7.5201
   66.7269    7.9149

　　

?

6.3.2网格数据插值

1、二维数据插值

其调用格式为

Zq=interp2(X, Y, V, Xq, Yq, method, extrapval)

X、Y分别存储采样点的平面坐标，V存储采样点采样值。

Xq、Yq存储插值点的平面坐标，Zq是根据相应的插值方法得到的插值点的值。

选项method的取值与一维插值函数相同，extrapval指定域外点的返回值。

【例6.17】表6.5所示为某企业从1968~2008年、工龄为10年、20年和30年的职工的月均工资数据。试用线性插值求出1973~1993年每隔5年、工龄为15年和25年的职工月平均工资。

 

 

 

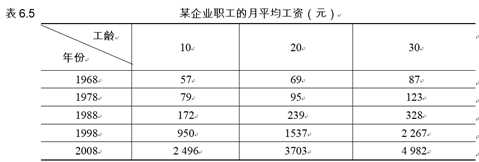
>> x=1968:10:2008;   %平面坐标的横坐标
>> h=[10:10:30].‘;   %平面坐标的纵坐标
>> W=[57,79,172,950,2496;
      69,95,239,1537,3703;
      87,123,328,2267,4982];
>> xi=1973:5:2003;   %存储采样点采样值
>> hi=[15;25];
>> WI=interp2(x,h,W,xi,hi)
WI =
   1.0e+03 *
    0.0750    0.0870    0.1462    0.2055    0.7245    1.2435    2.1715
    0.0935    0.1090    0.1963    0.2835    1.0928    1.9020    3.1223

　　

?

2. 多维数据插值

MATLAB提供了3维、N维插值函数interp3、interpn，用法与interp2 一致。

Vq=interp3(X, Y, Z, V, Xq, Yq, Zq, method)

Vq=interpn(X1, X2,…,Xn, V, Xq1, Xq2,…,Xqn, method)

interp3函数的输入参数X、Y、Z以及interpn函数的输入参数 X1、X2、X3、...、Xn必须是网格格式。

 

6.3.3散乱数据插值

vq = griddata(x,y,v,xq,yq,method)
?
vq = griddata(x,y,z,v,xq,yq,zq,method)
?
x、y、z存储采样点的坐标，v是与采样点的采样值
?
xq、yq、zq存储插值点的坐标，vq是根据相应的插值方法得到的插值结果。
?
选项method指定插值方法，可取值如下。
?
‘linear’（默认值）:基于三角剖分的线性插值、
‘nearest’：基于三角剖分的最近邻点插值、
‘natural’：基于三角剖分的三次自然邻点插值、 
‘cubic’：基于三角剖分的三次插值，仅支持二维插值、
‘v4‘：双调和样条插值，仅支持二维插值
?
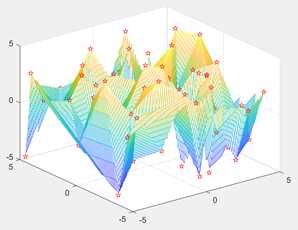
【例6.18】随机生成包含100个散点的数据集，绘制散点数据图和插值得到的网格数据图，观察插值结果。

xy=rand(100,3)*10-5;    
x = xy(:,1);
y = xy(:,2);
z = xy(:,3);
[xq,yq] = meshgrid(-4.9:0.08:4.9, -4.9:0.08:4.9);
zq = griddata(x,y,z,xq,yq);
mesh(xq,yq,zq)
hold on
plot3(x,y,z,‘rp‘)

　结果

 

 

 

6.4曲线拟合

polyfit函数的调用格式为
p = polyfit(x,y,n)
[p,S] = polyfit(x,y,n) 
[p,S,mu]=polyfit(X,Y,n)
x、y是两个等长的向量，存储采样点x和采样值y
产生一个n次多项式的系数向量p及其在采样点的误差向量S。p是一个长度为n + 1的向量，p的元素为多项式p1xn+p2xn−1+...+pnx+pn+1的系数。
mu是一个二元列向量，mu(1)是mean(x)， mu(2)是std(x)。
【例6.19】某研究所为了研究氮肥的施肥量对土豆产量的影响，做了十次实验，实验数据如表6.6所示。试分析氮肥的施肥量与土豆产量之间的关系
?

 

 

data=[0,15.18;34,21.36;67,25.72;101,32.29;135,34.03; ...
    202,39.45;259,43.15;336,43.46;404,40.83;471,30.75]; 
x=data(:,1);
y=data(:,2);
f=polyfit(x,y,2);
yi=polyval(f,x);
plot(x,y,‘rp‘,x,yi)
?

　　

6.5 非线性方程和非线性方程组的数值求解

6.5.1 非线性方程求解

求解一元连续函数F(x)的零点。
格式1：x=fzero(@fun,x0,options)     --->fun：函数名，x0：搜索起点。fzero只返回离x0最近的那个根。option为结构体变量。用于指定求解过程的优化参数。
格式2：[x,fval,exitflag,output]=fzero(@fun,x0,options)  --->fval返回目标函数在解x处的值，exitflag：返回求解过程终止原因，output ：返回寻根过程最优化的信息。
格式1为基本格式，格式2在函数寻根失败时返回寻根过程的错误和信息。

fzero的优化参数通常调用optimset函数设置，optimset函数的调用方法如下。options = optimset(优化参数1,值1, 优化参数2,值2,...)

 

 

 

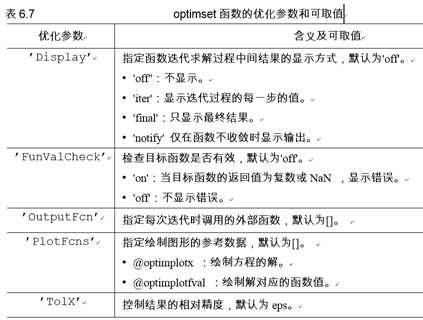
 【例6.20】求 e -2x - x =0在x0 = 0附近的根

fzero的优化参数通常调用optimset函数设置，optimset函数的调用方法如下。

options = optimset(优化参数1,值1, 优化参数2,值2,...)

（1）建立函数文件funx.m。

function fx=funx(x)

fx=exp(-2*x)-x;

　　

（2）调用fzero函数求根。

>> z=fzero(@funx,0.0)

z =

0.4263

　　

如果要观测函数求根过程，可先设置优化参数，然后求解，命令如下。

>> options=optimset(‘Display‘,‘iter‘);%设定显示迭代求解的中间结果

>> z=fzero(@funx,0.0,options);

　　

【例6.21】求下列非线性方程组在（0.5，0.5）附近的数值解。

 

 

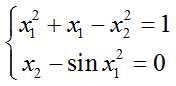
（1）建立函数文件myfun.m。

function q=myfun(p)

x1=p(1);

x2=p(2);

q(1)=x1^2+x1-x2^2-1;

q(2)=x2-sin(x1^2);

　　

（2）在给定的初值（0.5，0.5）下，调用fsolve函数求方程的根。

x0=[0.5;0.5];

options = optimoptions(‘fsolve‘,‘Display‘,‘off‘); %不显示中间结果

x= fsolve(@myfun,x0,options)

x =

0.7260

0.5029

　　

?