最大连续子数组和与JUnit测试

Posted 2021-02-17 cocoaman

• 【题目】最大连续子数组和（最大子段和）

  ---

• 背景

  问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为：Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
  例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
  -- 引用自《百度百科》

• 具体要求

  1. 要求写出可运行的完整代码提交至GitHub或者Coding.net系统中，并将代码地址附到博客内。
  2. 请从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖五个覆盖标准中，任选一个标准设计测试用例。
  3. 请利用自动测试工具对程序进行测试。
  4. 请将程序运行结果和自动测试分析结果截图附到博客中。

• 算法与代码实现

  抛弃的算法：通过题目要求，首先想到的是暴力求解，即利用循环，求出每一个子数组的值并进行比较，求出其中子数组的最大值。但是由于此方法效率较低，于是思考下一个方法。

  新的算法：我们首先分析出，当子数组和最大时，该子数组的首位和末位（存在的情况下），一定应为正值，且该子数组一定需要大于零才可作为新的最大的子数组并继续向下运算；否则，我们将抛弃他，并以下一位作为新的运算子数组。我们设每次运算的子数组为ThisSum，新的临时最大的子数组为MaxSum，根据此特性，可以列出公式：Array[i] = MAX（Array[i-1] + A[i] , A[i]）

根据上述公式，已将具体代码提交到GitHub上,便不在此赘述，点此查看Github源代码。

• 流程图与测试

根据写出的代码，画出流程图如下：

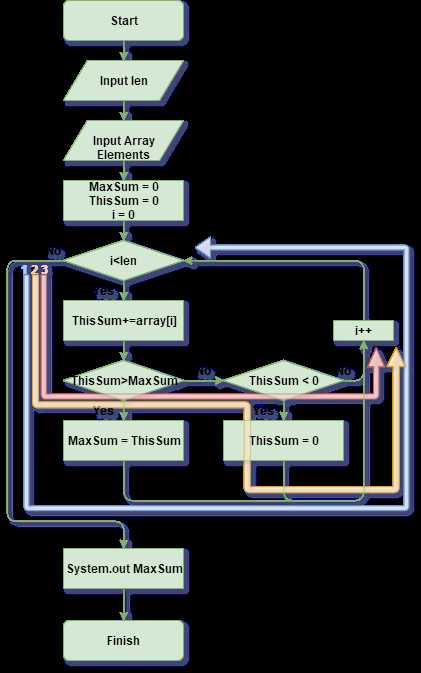
为了寻求合适而全面的测试样例，我找出循环内部的两条判断语句的流程，选用条件覆盖。

线段号	ThisSum>MaxSum	ThisSum<0
Blue1	Yes	—
Yellow2	No	Yes
Red3	No	No

选用的测试样例数组如下：

数组	备注
Array1：{ }	取边界值?测试
Array2：{1，-2，3，4，-5}	1->2->1->1->3
Array3：{1，2，3，4，5}	辅助测试
Array4：{-1，-2，-3，-4，-5}	全为负值 故最大为?

测试结果如下：
Array1：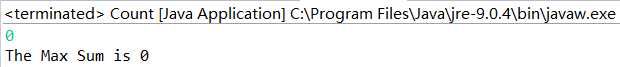

Array2：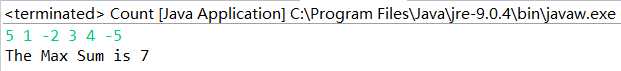

Array3：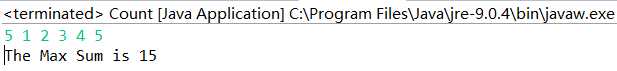

Array4：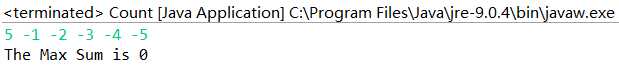

自动单元测试JUnitTest结果如下:

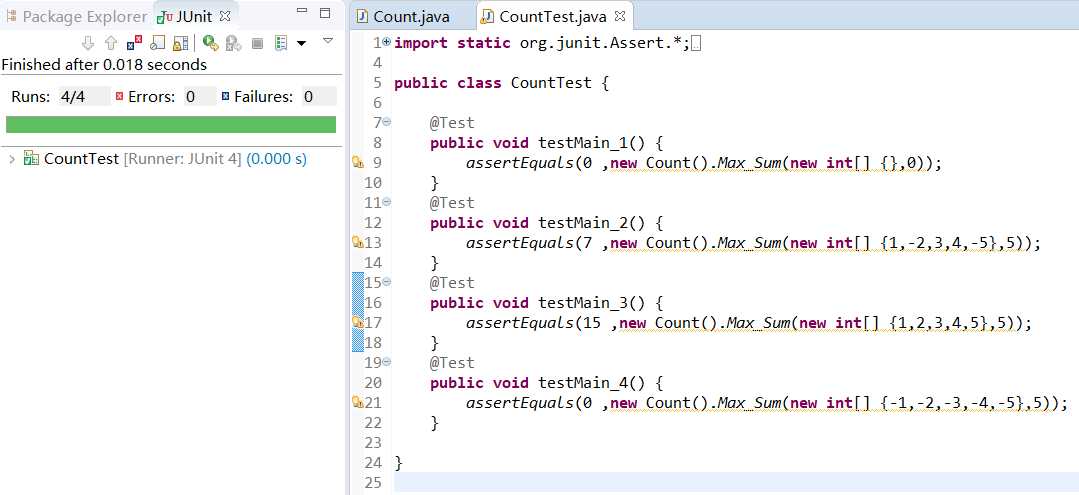
到此，对最大连续子数组求和的内容结束。