浅谈kmp

Posted 2021-02-16 greenpepper

一、废话不多说，首先直白的说kmp是什么？

　　先给你两个字符串，一个长的串一个短的串。 例：  abcdabccabca 与  cca，然后需要你求出第二个字符串在第一个字符串中的位置

暴力匹配的话大概就是下文的算法

 1 for( int i =0 ; i < str1len ; i++){
 2        int flag=1;
 3     for( int j = 0 ; j < str2len ; j++){
 4         if( str1[ i+j ] != str2[ j ]{
 5             flag=0;
 6             break;
 7         }
 8     }
 9     if(flag)printf("%d ",i);
10 }
11 //strl1len 指length of string 1 也就是字符串1的长度。
12 //str1 指第一个字符串
13 //通常，在字符串匹配中，作者，默认：长串：str1，短串：str2

View Code

这种算法是大多数人都能想到的，时间复杂度约为O（mn）mn分别是两个字符串长度。

　　而kmp算法就是针对这种串匹配问题的一种优化算法。

叫kmp的原因是因为发明这个算法的人三个巨巨名字首字母是分别kmp

继续读下去之前，请先确保对暴力匹配的算法进行理解。

二、为什么用kmp？

　　kmp算法的核心在于对已匹配的信息充分利用。好吧，这么说太抽象了，举个具体的栗子吧。

　　假设我们的第二个字符串是这样的。

　　

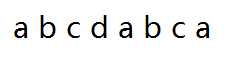
　　在与第一个字符串比较的时候，我们分别有两个字母， i代表在字符串1中匹配当前起始位置，j代表字符串2中匹配的位置。也就是上面暴力匹配代码中的str1 [ i+j ] == str2[ j ];

　　现在假设我们字符串2中匹配到了这个位置 

　

　　然后检测到不同，那么我们是不是应该将j回到头呢？不是的。

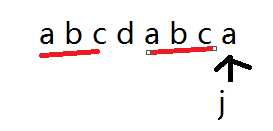　　红色划线部分是相同的对吧。这也就是意味着，如果我们j匹配到箭头所指的abc

　　那么在字符串1中的i+j-1 i+j-2 i+j-3这三个元素一定也是abc。为什么？ 因为我匹配过了啊。这就是我们所得到的已知信息。

　　我们还已知什么呢？

　　字符串2中的头三个字母 和目前失配的前三个字母是相同的。于是乎，我们可以把j移到前三个abc的后面也就是下图

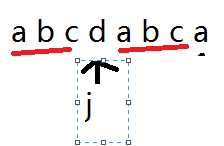　　为什么？  因为你匹配到的当前后缀与str2的前缀有公共部分。所以匹配时，这些公共部分就可以当做匹配过。

　　（后缀：就是从后往前的字符串，比如这个就是 a,ca,bca，直白的说就是后几个）

　　（前缀：从前往后的字符串，比如a,ab,abc，直白的说就是前几个）

　　这么做的好处是i每次到可以每次更新到i+j,不用回溯了。每次i只管往前走就行，j自己玩去。我们就省了很多的回溯时间。

　　那么你一定又有一个疑问了。该怎么做呢？我怎么知道回到哪去呢???

三、怎么整这个算法啊？？

　　向下阅读请先对上方原理进行理解。

　　那么我们可以着手上方的问题了，怎么知道可以回到哪去呢？

从下文起，i指目前匹配到的所在str1的位置， j 指目前匹配到 所在str2 的位置

　　我们可以开出一个数组，在匹配前先对str2的每一位进行计算，也就是如果是第一位失配我该回到哪？第二位失配我该回到哪？and so on...

　　读者在此像大部分kmp教程一样，将这个(对应了str2中，解释每一位该回到前面哪里去，也可以说是前缀和后缀的最长相同区域的)数组称作 next【】数组。

　　比如还是上面那个字符串

　　

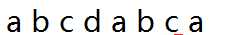
　　我们要求出他的每一位

　　如果我们第一位失配，好吧我们别无选择，i进行下一位匹配吧，j不变。

　　如果第二位失配，我们可以得到信息，b ，和前缀a不同。我们j回到最初的起点，（i到下一位）。

　　如果第三位失配，我们已知信息中，第二位头不是a，所以无法匹配，所以i可以继续下一位。

　　也就是说

　　next[1] next[2] next[3]都是0， 直接回到了0处。

　　以此类推，我们可以得到next数组为{0,0,0,0,0,1,2,3,}

　　为了检测 j 在0点失配，我们规定 next[0]=-1；

　　同时我们也可以发现，在求next数组时如果前一位最长前后缀是a，后一位也与前一位最长前缀的下一位匹配了，那么它的最长前后缀显然是a+1;

　　比如 abcdab时，最长前后缀是2 当到下一位 abcdabc时，多出的c这一位与前一位前缀最后一位（绕的有点晕）.

　　就是说 abcdab 中的 前缀abc只有ab与后缀 dab的ab匹配了，那么  前缀ab的后一位c 与后缀的多出的一位c匹配, 这个多出的位最长公共前后缀就是比前一位多一位。

好了，这就是next数组的求法，下面给出代码。

void get_next()
{
    int i = 0, j = -1;
    nexxt[0] = -1;                         //对第一位初始化为-1；
    while (str2[i] != ‘‘) 
       {
        while (j != -1 && str2[i] != str2[j])//如果前后缀不相同了，
            j = nexxt[j];                      //看上一个最长前后缀
        
                nexxt[++i] = ++j;            //更新当前前后缀。
    }
}

有了这个数组，使用原理在第二部分也说过了，那么直接上使用的代码吧。

int kmp_1()
{
    int i=0,j=0;                              //各自从各自数组起点出发
    while(str1[i]!=‘‘)                   //检测字符串1是否到尾部
    {
        if(j==-1||str1[i] == str2[j] ){ //如果匹配，或者j在头开始的
            if(str2[j+1]==‘‘)          //检测字符串2是否到尾，到了就说明
            {                                   //已经完全匹配了
                return i-j+1;              //返回字符串2在1 的位置
            }
            else j++;                      //没到头就继续匹配下一位
            i++;
        }
        else j=nexxt[j];                //j自己向前走，直到有公共前后缀，或
    }                                         //回到0处。

    return -1;                       //str1都匹配完了还没找到，只好返回-1咯
}

！！！注意：以上检测代码尾部的时候，若对时间要求高，则需要将检测尾部的

str1[i]!=‘‘  和   str2[j+1]==‘‘  
提前将两个字符串长度存下来，也就是 i<str1len   j+1<str2len，
否则会像我一样超时到自闭

 

 四、完整代码

　　以下代码可以直接当做模板

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 using namespace std;
 5 int nexxt[100000005];
 6 char str2[100000005];
 7 char str1[100000005];
 8 int str1len, str2len;
 9 void get_next()
10 {
11     int i = 0, j = -1;
12     nexxt[0] = -1;
13     while (i < str2len) {
14         while (j != -1 && str2[i] != str2[j])
15             j = nexxt[j];
16         nexxt[++i] = ++j;
17     }
18 }
19 int kmp_1()
20 {
21     int i = 0, j = 0;
22     while (i < str1len)
23     {
24         if (j == -1 || str1[i] == str2[j]) {
25             j++;
26             i++;
27             if (j == str2len)return i - j + 1;
28         }
29         else j = nexxt[j];
30     }
31     return -1;
32 }
33 int main()
34 {
35     int n, a, b;
36     cin >> n;
37     while (n--)
38     {
39         getchar();
40         cin.getline(str1, 100000000, ‘
‘);
41         cin.getline(str2, 100000000, ‘
‘);
42         str1len = strlen(str1);
43         str2len = strlen(str2);
44         get_next();
45         cout << kmp_1() << endl;
46     }
47     return 0;
48 }