从KMP到AC自动机

Posted 2021-02-13 xu-daxia

不想写题。不如写写算法总结？

KMP

介（che）绍（dan）

以前都不知道(KMP)为什么叫(KMP)，现在才明白：该算法是三位大牛：D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的，以其名字首字母命名。
(KMP)可以在(O(n+m))的时间复杂度内解决判定一个字符串(A[1)~ (N])是否为字符串(B[1)~(M])的字串的问题。
虽然Hash好像也可以线性解决这个问题

我会暴力

当然一个(O(nm))的做法是非常显然的：直接枚举A串在B串的开始位置然后往后一位一位的比较。
考虑这样的做法有什么可以优化的地方？
考虑如下场景，某次匹配中按(O(nm))的方法进行到这一步。
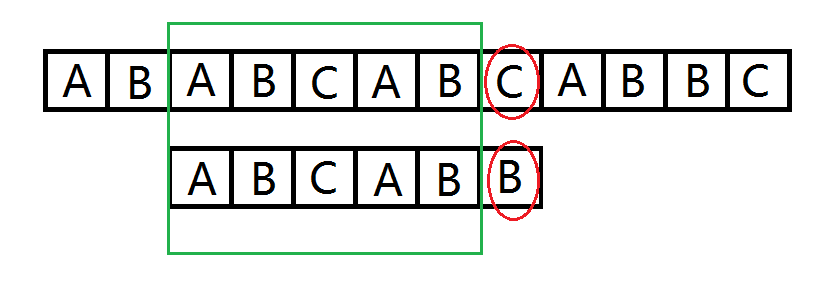图中下方是串(A),上方是串(B)，我们已经匹配到最后一个字符，匹配就快成功，但不幸的是最后一位出错了，我们又要从头匹配。
但是

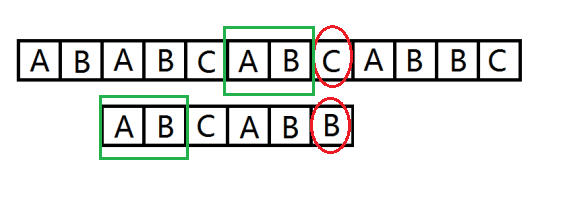
我们发现绿框框住的部分匹配，但我们之后还要重新匹配浪费了时间。我们能不能记录一些信息，然后下次直接从绿框后面的位置开始匹配，这样不就节约了时间。
还有，能不能选出一些可能完成匹配的位置进行匹配，这样就不用从每一个位置匹配整个串，也节约了时间。
(KMP)算法就这样诞生了

算法流程

KMP算法定义了一个next数组。
其中next[i]表示A中以i结尾的非前缀子串和A的前缀能匹配的最长长度。
那么这个东西有什么用啊?感觉好玄妙，为什么非要是非前缀？
别急我们先来说说(next)数组的求法。
我会(O(n^2))的求法。。。
其实可以(O(n))求。

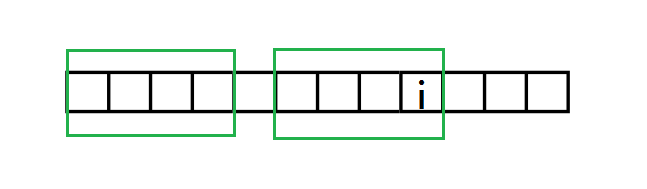
假设我们已经求出了next 1~next i，图中绿框框起来的就是能匹配的最长的A中以i结尾的非前缀子串和A的前缀。
我们现在要求(next[i+1])。

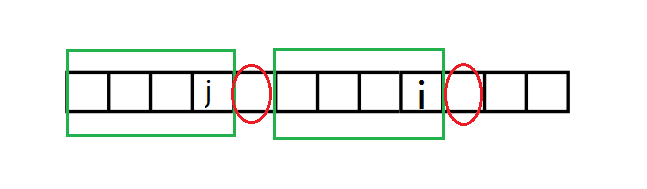
(这里的j就相当于(next[i]))
显然当两个红圈圈起的位置上的字符相等，那么(next[i+1]=j+1)
那么不相等怎么办？
重新匹配吗，那不就(O(n^2))了吗？
我不会了妈妈救我

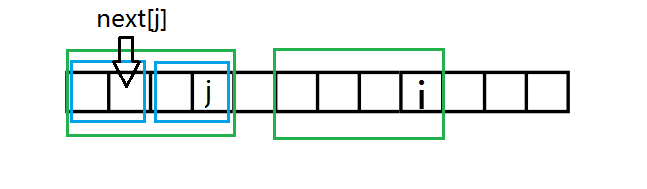
我们先设出(next[j])的位置。显然两个蓝框框起的串匹配

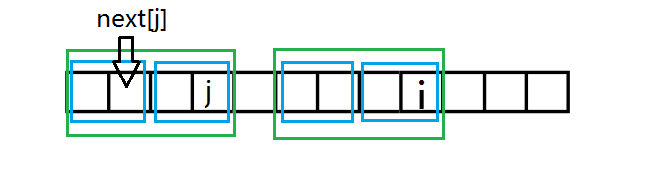
因为绿框框起的串匹配，是不是四块蓝框框起的串互相匹配。

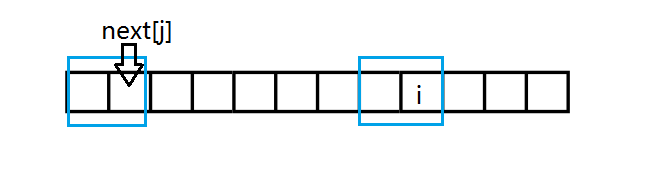
四块都互相匹配了显然这两块是匹配的。
咦，等等，好像有点眼熟！
这跟开始的一张图片很像。
也许你已经猜到接下来该做什么了。
我们看看(next[j]+1)和(i+1)位置上的字符是否相等。如果相等(next[i+1]=next[j]+1)，如果还不相等我们把(next[j])再变成(next[next[j]])。。。。。。（一直这样跳(next)跳下去）
知道最后找到一个字符跟(i+1)位置上的字符相等。或找不到字符跟(i+1)位置上的字符相等(next[i+1])就是0。
这样的正确性有保证吗？
我们想一直跳(next)实际上就是在遍历（所有能匹配的A中以i结尾的非前缀子串和A的前缀的长度）（名词太长用括号括起来）。因为(next)要求是最长长度，所以可以不重不漏遍历所有情况。
或者这样想

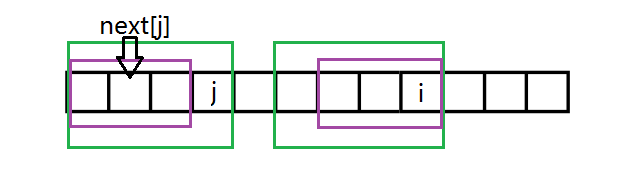
如果漏掉了紫色框的情况。即假设紫色框框起的部分是(长度比绿框小的是最长的能匹配的最长的A中以j结尾的非前缀子串和A的前缀)

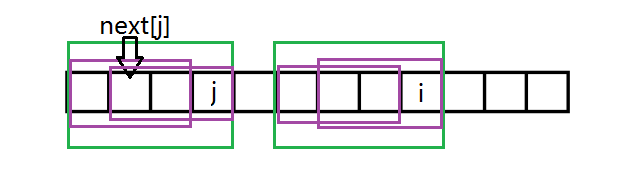
那么因为绿框框起的串匹配，四个紫框框起的串互相匹配。
然后next[j]就不在图中所在位置了，也就是说与(next[j])代表A中以j结尾的非前缀子串和A的前缀能匹配的最长长度矛盾。
所以用上面说的方法正确性是对的。
那这样感觉复杂度又成(O(n^2))的了
其实是(O(n))的，我们来分析一波
这是求(next)数组的代码

for(int i=2,j=0;i<=len;i++){
    while(j&&A[j+1]!=A[i])j=nxt[j];
    if(A[j+1]==A[i])j++;
    nxt[i]=j;
}

每次求(next[i])时我们程序里的记录(next[i])的变量(j)最多+1，一共最多加n次。然后每次跳(next)，j只会减小。
所以最多跳(n)次(next)。复杂度(O(n))。
至此我们终于把如何求(next)数组讲完了。
其实后面的就简单了。
我们回到最初的起点。。
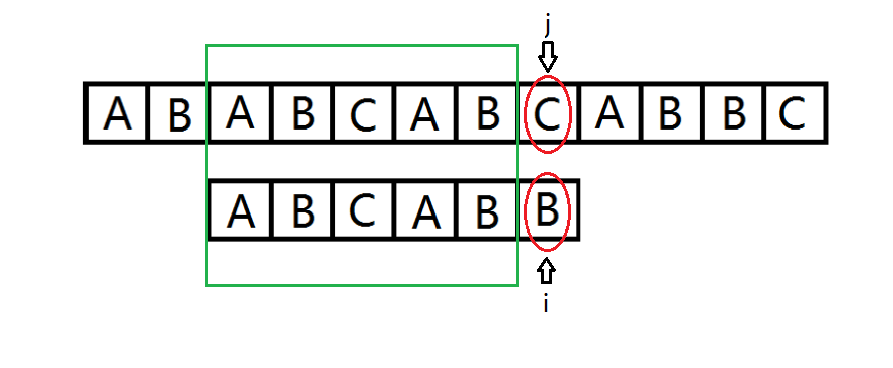我们依然是按位匹配两个串。当不匹配的时候。我们把i改成next[i]继续匹配就好。
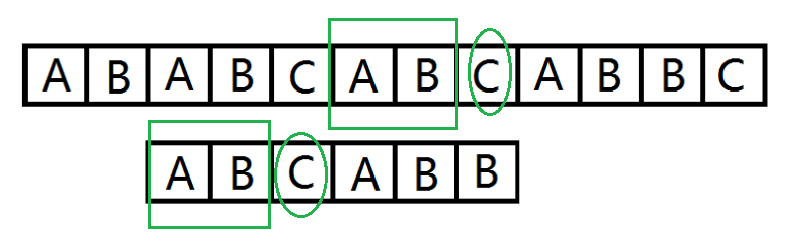就像这样。
板子题
# P3375 【模板】KMP字符串匹配

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=1010000;
char s1[N],s2[N];
int len1,len2,nxt[N];
int main(){
    scanf("%s",s1+1);
    scanf("%s",s2+1);
    len1=strlen(s1+1);
    len2=strlen(s2+1);
    for(int i=2,j=0;i<=len2;i++){
        while(j&&s2[j+1]!=s2[i])j=nxt[j];
        if(s2[j+1]==s2[i])j++;
        nxt[i]=j;
    }
    for(int i=1,j=0;i<=len1;i++){
        while((j&&s2[j+1]!=s1[i])||j==len2)j=nxt[j];
        if(s2[j+1]==s1[i])j++;
        if(j==len2)printf("%d
",i-j+1);
    }
    for(int i=1;i<=len2;i++)printf("%d ",nxt[i]);
    return 0;
}

持续更新ing。。。