Z字形编排问题详解(C++)

Posted 2021-02-12 suchang

Z字形编排问题详解(C++):

问题描述：给定一个矩阵matrix，输出矩阵matrix进行Z字形编排后的内容。

原矩阵：

                  

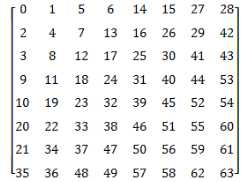
输出形式：

             

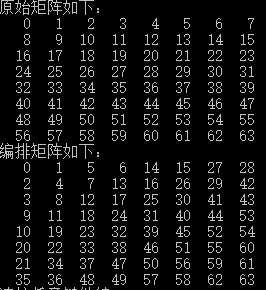
算法分析与详细解答：

      要解决这样一个问题，可能一开始无从下手，但是我们只要认真观察Z字形矩阵的走向过程，就不难发现其中的规律。对于原始矩阵matrix中的任意元素 matrix[i][j]的遍历走向规律可以分为以下三种情况：

       1、如果矩阵的元素matrix[i][j]中纵坐标j是偶数，并且i==0或i==SIZE-1,那么遍历路径在矩阵中的走向就是向右移动一格。

       2、如果矩阵的元素matrix[i][j]中横坐标i是奇数，并且j==0或j==SIZE-1,那么遍历路径在矩阵中的走向就是向下移动一格。

       3、除以上规律情况之外，如果矩阵的元素matrix[i][j]的横纵坐标之和i+j为偶数，那么遍历路径在矩阵中的走向就是向右

            上角移动一格；否则，如果i+j是奇数，那么遍历路径在矩阵中的走向就是向左下角移动一格。

c++代码：

#include<iostream>
#include<iomanip>
using namespace std;
const int SIZE = 8;
int main()
{
    int matrix[SIZE][SIZE]= { 0 };
    int a[SIZE][SIZE] = { 0 };
    int* ptr = &(matrix[0][0]);
    for (int i = 0; i < SIZE*SIZE; i++) 
        *ptr++ = i;
    cout << "原始矩阵如下：" << endl;
    for (int i = 0; i < SIZE; i++) 
    {
        for (int j = 0; j < SIZE; j++) 
            cout << setw(4) << *(*(matrix + i) + j);
        cout << endl;
    }
//进行Z-字形编排
    int i = 0, j = 0;
    for (int x = 0; x < SIZE; x++)
    {
        for (int y = 0; y < SIZE; y++) {
            *(*(a + i) + j) = *(*(matrix + x) + y);
            if ((i == 0 || i == SIZE - 1) && j % 2 == 0)
            {
                j++;
                continue;
            }
            if ((j == 0 || j == SIZE - 1) && i % 2 == 1)
            {
                i++;
                continue;
            }
            if ((i + j) % 2 == 0) {
                i--;
                j++;
            }
            else if ((i + j) % 2 == 1) {
                i++;
                j--;
            }
        }
    }
    cout << "编排矩阵如下：" << endl;
    for (int k = 0; k < SIZE; k++)
    {
        for (int  h= 0; h < SIZE; h++)
            cout << setw(4) << *(*(a + k) + h);
        cout << endl;
    }
    system("pause");
    return 0;
}

欢迎大家评论！