DP 斜率优化题目/决策单调性题目
Posted saigyouji-yuyuko
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了DP 斜率优化题目/决策单调性题目相关的知识,希望对你有一定的参考价值。
斜率优化
冬令营讲到了dp斜率优化后瞎写了一些斜率优化,因为毕竟上次写是老早以前了,当时对这个并不是很理解,现在有一点数学基础,稍微好一点了。
瞎找的斜率优化题,可能有点太水了,我这种这么菜的人竟然都切得那么快。可能难度不够,因为有个y坐标不单调要套个平衡树的我是真不会,这个嘛以后再说了。
1.hdu3507 Print Article
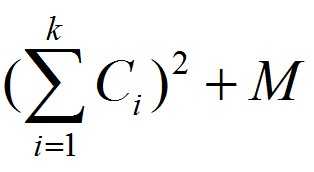 给定非负数列,划成若干块,每块价值是左边那玩意儿。求总权值min.
给定非负数列,划成若干块,每块价值是左边那玩意儿。求总权值min.
这个自己写写就可以搞出来了吧,现在看真心不难,除非数值有负的。。那个要平衡树,现在写不动。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 5 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 6 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 7 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 8 template<typename T>inline T read(T&x){ 9 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c==‘-‘)f=1; 10 while(isdigit(c))x=x*10+c-‘0‘,c=getchar();return f?x=-x:x; 11 } 12 const int N=500000+7; 13 ll f[N],C[N],m; 14 int q[N],l,r,n; 15 inline ll Getx(int i){return C[i];} 16 inline ll Gety(int i){return f[i]+C[i]*C[i];} 17 18 int main(){//freopen("test.in","r",stdin);//freopen("test.out","w",stdout); 19 while(~scanf("%d%lld",&n,&m)){ 20 q[l=r=1]=0,f[0]=0; 21 for(register int i=1;i<=n;++i){ 22 read(C[i]),C[i]+=C[i-1]; 23 while(l<r&&(Gety(q[l+1])-Gety(q[l]))<=2*C[i]*(Getx(q[l+1])-Getx(q[l])))++l; 24 f[i]=f[q[l]]+(C[i]-C[q[l]])*(C[i]-C[q[l]])+m; 25 while(l<r&&(Gety(q[r])-Gety(q[r-1]))*(Getx(i)-Getx(q[r]))>=(Gety(i)-Gety(q[r]))*(Getx(q[r])-Getx(q[r-1])))--r; 26 q[++r]=i; 27 } 28 printf("%lld ",f[n]); 29 } 30 return 0; 31 }
2.P2365 任务安排
注意一个费用提前计算的思想,就是为了简化维度,并没有明显规定要画成多少块,但块数对f有影响,那可以提前计算对之后的费用加上去,这也应当是对的dp.详见李煜东书上的dp斜率优化。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N=5000+7; 5 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 6 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 7 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 8 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 9 template<typename T>inline T read(T&x){ 10 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c==‘-‘)f=1; 11 while(isdigit(c))x=x*10+c-‘0‘,c=getchar();return f?x=-x:x; 12 } 13 ll f[N],t[N],c[N],S; 14 int l,r,n,q[N]; 15 16 int main(){//freopen("tmp.in","r",stdin);freopen("tmp.out","w",stdout); 17 read(n),read(S); 18 for(register int i=1;i<=n;++i)t[i]=read(t[i])+t[i-1],c[i]=read(c[i])+c[i-1]; 19 f[l=r=1]=0; 20 for(register int i=1;i<=n;++i){ 21 while(l<r&&f[q[l+1]]-f[q[l]]<=(S+t[i])*(c[q[l+1]]-c[q[l]]))++l; 22 f[i]=f[q[l]]+S*(c[n]-c[q[l]])+t[i]*(c[i]-c[q[l]]); 23 while(l<r&&(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])<=(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]]))--r; 24 q[++r]=i; 25 } 26 printf("%lld ",f[n]); 27 return 0; 28 }
3.P3628 特别行动队
没什要说的,斜率的上凸的优化。斜率负的小心点就行了。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 5 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 6 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 7 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 8 template<typename T>inline T read(T&x){ 9 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c==‘-‘)f=1; 10 while(isdigit(c))x=x*10+c-‘0‘,c=getchar();return f?x=-x:x; 11 } 12 const int N=1000000+7; 13 ll f[N],S[N],a,b,c; 14 int n,l,r,q[N]; 15 inline ll fy(int i){return f[i]+a*S[i]*S[i]-b*S[i];} 16 inline ll fx(int i){return S[i];} 17 18 int main(){//freopen("tmp.in","r",stdin);freopen("tmp.out","w",stdout); 19 read(n);read(a),read(b),read(c);q[l=r=1]=0; 20 for(register int i=1;i<=n;++i){ 21 S[i]=S[i-1]+read(S[i]); 22 while(l<r&&fy(q[l+1])-fy(q[l])>=2*a*S[i]*(fx(q[l+1])-fx(q[l])))++l; 23 f[i]=f[q[l]]+a*(S[i]-S[q[l]])*(S[i]-S[q[l]])+b*(S[i]-S[q[l]])+c; 24 while(l<r&&(fy(i)-fy(q[r]))*(fx(q[r])-fx(q[r-1]))>=(fy(q[r])-fy(q[r-1]))*(fx(i)-fx(q[r])))--r; 25 q[++r]=i; 26 } 27 printf("%lld ",f[n]); 28 return 0; 29 }
4.BZOJ3156 防御准备亦无甚要说。longlong注意。状态设计多想想就行,$f_i$表示的是i建塔,从1到i总最小费用,然后转移就简单了。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 typedef double db; 5 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 6 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 7 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 8 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 9 template<typename T>inline T read(T&x){ 10 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c==‘-‘)f=1; 11 while(isdigit(c))x=x*10+(c&15),c=getchar();return f?x=-x:x; 12 } 13 const int N=1000000+7; 14 ll f[N],a[N]; 15 int q[N],n,l,r; 16 inline ll y(int j){return f[j]+(1ll*j*(j+1)>>1);} 17 18 int main(){//freopen("tmp.in","r",stdin);freopen("tmp.out","w",stdout); 19 read(n);for(register int i=1;i<=n;++i)read(a[i]); 20 q[l=r=1]=0; 21 for(register int i=1;i<=n;++i){ 22 while(l<r&&y(q[l+1])-y(q[l])<=1ll*i*(q[l+1]-q[l]))++l; 23 f[i]=f[q[l]]+(1ll*(i-q[l])*(i-q[l]-1)>>1)+a[i]; 24 while(l<r&&(y(i)-y(q[r]))*(q[r]-q[r-1])<=(y(q[r])-y(q[r-1]))*((ll)i-q[r]))--r; 25 q[++r]=i; 26 } 27 printf("%lld ",f[n]); 28 return 0; 29 }
5.咕咕咕。。
以上是关于DP 斜率优化题目/决策单调性题目的主要内容,如果未能解决你的问题,请参考以下文章
bzoj4518: [Sdoi2016]征途(DP+决策单调性分治优化)
