复习backtracking 并总结

Posted 2021-02-08 keepac

每一个分支把leetcode backtracking 几十个题目重新复习一遍，领略back tracking 精髓。

 

一 排列问题： 

46/47 Permutations ： 46 没有重复数字 47 包含重复数字

46： 关键是采用used[i] 来标记一个i 是否已经被选择了， 注意used 状态改变只对子节点状态有效，对 同一层的节点状态是无效的，这也是back tracking 精髓之一。

例如下面最后一个不能放1， 是因为第一层 1 被used 了并且传递到了第三层。

 

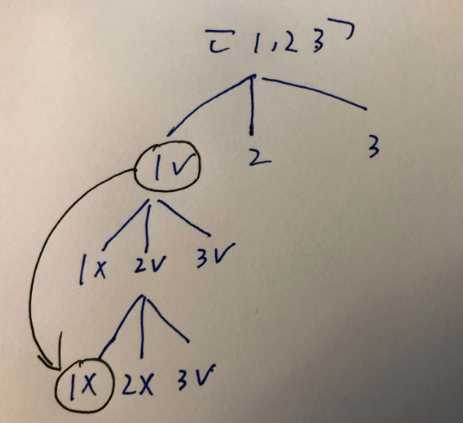
47 有重复元素关键是去重

1. 排序 

2. if(used[i]) continue;    --C1

    if(i>0 && used[i-1] == used[i] && !used[i]) continue   --C2

第二个if 的理解是 ：是否选择 一个数字的原则   当前 i , 如果和 i-1 重复， 那么选择i 是因为 选择了 i-1, 如果没选择  i-1 就不要再选择 i了。

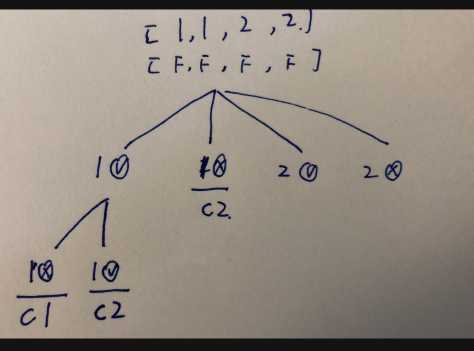
第一层第二个1 不被选择是因为 condition 2, 因为 used 初始化都为False, 因为这  i-1 没有被选择，因此不能选择 这个1

第二层第一个1 没被选择因为 condition 1, 因为 used[i] 已经为true 了

第二层第而个1 被选择 因为condition 2, 因此第一层的第一个1 被选择了。

 

结果数目， 对于排列问题46 自然是 n! 个结果， 对于 47， 主要看重复数字个数  比如 ABBBCCD ， 结果为7！/(3!2!) 

 

 

二 组合问题：

77 从1~n 中产生K个组合， 因为1~n 没有重复元素，也就是求 C(n,k) 所以很简单

 

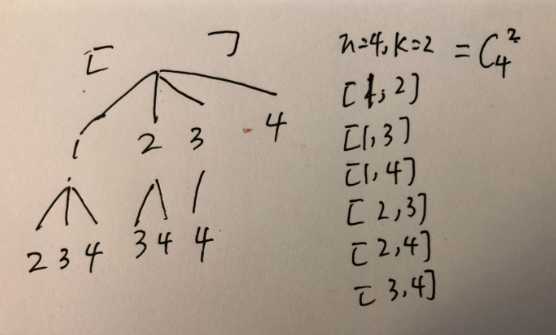
40 题目：有重复的数组里，求和为target 的

Input: candidates = [10,1,2,7,6,1,5], target = 8,
A solution set is:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

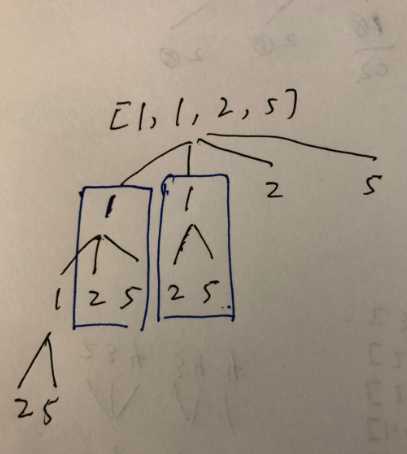
从这个递归树可以看出， 对于有重复数字只需要拿第一个构建递归树就好了，后面重复数字构建的树一定包含在了前面的tree 里。
因此去重的条件是：
if(i>start && nums[i] == nums[i-1]) continue. 
为何需要 i> start, 如果没有这个条件 第二层的 1就会不存在了。 也就是对于重复数字永远都放第一个就好了。

 

 三  subsets 问题 又叫power sets（2^n）

78题：

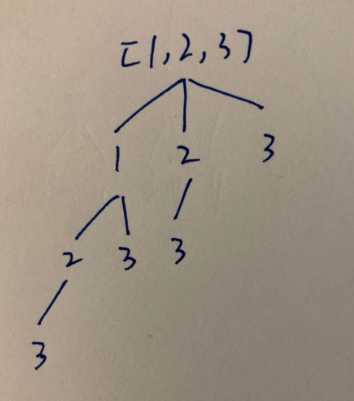
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

 

从递归树看出基本和 组合问题是一样的， 区别在于每次递归都得结果都是放到最终的结果离去，并且递归不需要return 条件，所有的情况都走完就可以了。

 

 

 

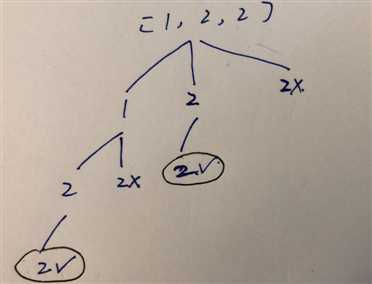
90 题：  78题去重，去重条件和 40题的去重条件一摸一样：  if(i!=start && nums[i] == nums[i-1]) continue;
要点在于 每一个分支的第一个元素必然要放：i != start

 

总结： 

1. 排列问题模板： 每次问题的规模都是从 0~n-1,因此得有返回条件否则算法不会终止。

1         for(int i=0; i<nums.length; i++){
2             if(!used[i]){     
3                curResult.add(nums[i]);
4                used[i] = true;
5                backTracking(curResult, result,nums,used);
6                used[i] = false;
7                curResult.remove(curResult.size()-1);         
8             }
9         }

2. 排列问题去重的条件：

if(used[i] || i>0 && nums[i]==nums[i-1] && !used[i-1]) continue

 

2. 组合问题和 power set 都是 需要一个start 每次递归都是从 上一层的 i+1 开始：

1         for(int i=start; i<nums.length; i++){
2            // if(i==start || i>start && nums[i]!= nums[i-1]){
3             if(i!=start && nums[i] == nums[i-1]) continue;
4             curResult.add(nums[i]);
5             dfs(i+1, curResult, result,nums);
6             curResult.remove(curResult.size()-1);
7           
8         } 

3. 排列和 power set 就算都没有return 条件， 算法也是可以终止的， 最多只有 2^n 次，  因此 dfs(i+1,....) 会让规模越来愈小。 而排列问题每次问题的规模都是一样，如果没有返回条件是不会终止的。