fzyzojP3782 -组合数问题
Posted miracevin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了fzyzojP3782 -组合数问题相关的知识,希望对你有一定的参考价值。
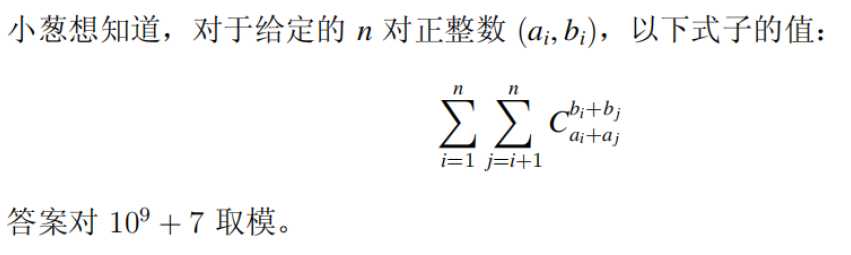
![]()
这个ai<=2000有点意思
启发我们用O(W^2)的算法
FFT不存在,对应关系过紧
考虑组合意义转化建模,再进行分离


(除以2不需要逆元不懂为啥,但是算个逆元总不费事)
由于终点可能在起点的右下,所以,从左上到右下要再做一遍
但是每个终点正上方的起点统计了两次,再减掉即可
(注意大力卡常:
1.s2[i][j]没有,就不用算了
2.f,ans开long long 尽量减少取模
3.组合数用阶乘计算
)
#include<bits/stdc++.h> #define il inline #define reg register int #define numb (ch^‘0‘) using namespace std; typedef long long ll; il void rd(int &x){ char ch;bool fl=false; while(!isdigit(ch=getchar()))(ch==‘-‘)&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=4000+4; const int M=200000+5; const int mod=1e9+7; ll f[N][N]; int s1[N][N],s2[N][N]; int jie[N],inv[N]; int qm(int x,int y){ int ret=1; while(y){ if(y&1) ret=(ll)ret*x%mod; x=(ll)x*x%mod; y>>=1; } return ret; } ll mo1(ll x){ return x>=4e12?x%mod:x; } ll mo2(ll x){ return x>=0?x%mod:x; } int n; int C(int n,int m){ return (ll)jie[n]*inv[m]%mod*inv[n-m]%mod; } int main(){ rd(n); int a,b; jie[0]=1; for(reg i=1;i<=4000;++i) jie[i]=(ll)jie[i-1]*i%mod; inv[4000]=qm(jie[4000],mod-2); for(reg i=3999;i>=0;--i) inv[i]=(ll)inv[i+1]*(i+1)%mod; ll ans=0; for(reg i=1;i<=n;++i){ rd(a);rd(b); int x=a-b+2000,y=b+2000; s1[x][y]++; x=-a+b+2000,y=-b+2000; s2[x][y]++; ans=mo2(ans+mod-C(2*a,2*b)); } ans%=mod; /// cout<<ans<<endl; for(reg i=4000;i>=1;--i){ for(reg j=4000;j>=1;--j){ f[i][j]=mo1(f[i+1][j]+f[i][j+1]+s1[i][j]); if(s2[i][j])ans=mo2(ans+(ll)f[i][j]*s2[i][j]); } } ans%=mod; // cout<<ans<<endl; for(reg i=1;i<=4000;++i){ for(reg j=4000;j>=1;--j){ f[i][j]=mo1(f[i-1][j]+f[i][j+1]+s1[i][j]); ans=s2[i][j]?(ans+(ll)f[i][j]*s2[i][j])%mod:ans; s1[i][j]+=s1[i][j+1]; ans=s2[i][j]?(ans-(ll)s1[i][j]*s2[i][j]+(ll)10*mod)%mod:ans; } } ll inv2=5e8+4; ans=ans*inv2%mod; printf("%lld",ans); return 0; } } signed main(){ freopen("3782.in","r",stdin); freopen("3782.out","w",stdout); Miracle::main(); return 0; } /* Author: *Miracle* Date: 2019/2/8 18:52:17 */
总结:
核心:转化问题,分离终点和起点
和这个题的最后差分分离思路有异曲同工之处:AGC 018E.Sightseeing Plan——网格路径问题观止
以上是关于fzyzojP3782 -组合数问题的主要内容,如果未能解决你的问题,请参考以下文章