数组中的逆序对

Posted 2021-02-08 tianzeng

题目

　　在数组中的两个数字如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

思路

一，直接求解

　　顺序扫描整个数组。每扫描到一个数字的时候，逐个比较该数字和它后面的数字的大小。如果后面的数字比它小，则这两个数字就组成了一个逆序对。假设数组中含有n 个数字。由于每个数字都要和O(n）个数字作比较， 因此这个算法的时间复杂度是O(n^2)。

二，分析法

　　我们以数组｛7, 5, 6, 4｝为例来分析统计逆序对的过程。每次扫描到一个数字的时候，我们不能拿它和后面的每一个数字作比较，否则时间复杂度就是O(n^5)，因此我们可以考虑先比较两个相邻的数字。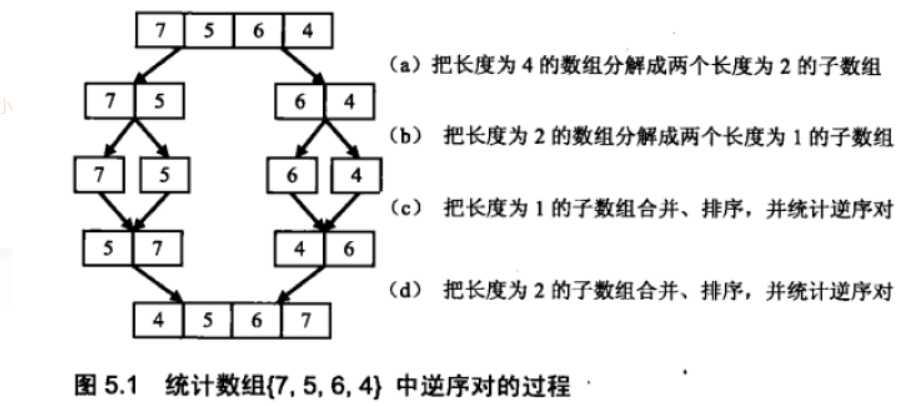

如图5 . 1 ( a )和图5.1 ( b）所示，我们先把数组分解成两个长度为2的子数组， 再把这两个子数组分别拆分成两个长度为1 的子数组。接下来一边合并相邻的子数组， 一边统计逆序对的数目。在第一对长度为1 的子数组｛7｝、｛5｝中7 大于5 ， 因此（7, 5）组成一个逆序对。同样在第二对长度为1 的子数组｛6｝、｛4｝中也有逆序对（6, 4）。由于我们已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组排序（ 图5.1 ( c）所示），以免在以后的统计过程中再重复统计。

(a) 把长度为4的数组分解成两个长度为2的子数组；
(b) 把长度为2的数组分解成两个成都为1的子数组；
(c) 把长度为1的子数组合并、排序并统计逆序对；
(d) 把长度为2的子数组合并、排序，并统计逆序对；
       在上图（a）和（b）中，我们先把数组分解成两个长度为2的子数组，再把这两个子数组分别拆成两个长度为1的子数组。接下来一边合并相邻的子数组，一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7大于5，因此（7,5）组成一个逆序对。同样在第二对长度为1的子数组{6}、{4}中也有逆序对（6,4）。由于我们已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组排序如上图（c）所示，以免在以后的统计过程中再重复统计。
      接下来我们统计两个长度为2的子数组子数组之间的逆序对。合并子数组并统计逆序对的过程如下图如下图所示。
      我们先用两个指针分别指向两个子数组的末尾，并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个数组中的数字，则构成逆序对，并且逆序对的数目等于第二个子数组中剩余数字的个数，如下图（a）和（c）所示。如果第一个数组的数字小于或等于第二个数组中的数字，则不构成逆序对，如图b所示。每一次比较的时候，我们都把较大的数字从后面往前复制到一个辅助数组中，确保辅助数组（记为copy）中的数字是递增排序的。在把较大的数字复制到辅助数组之后，把对应的指针向前移动一位，接下来进行下一轮比较。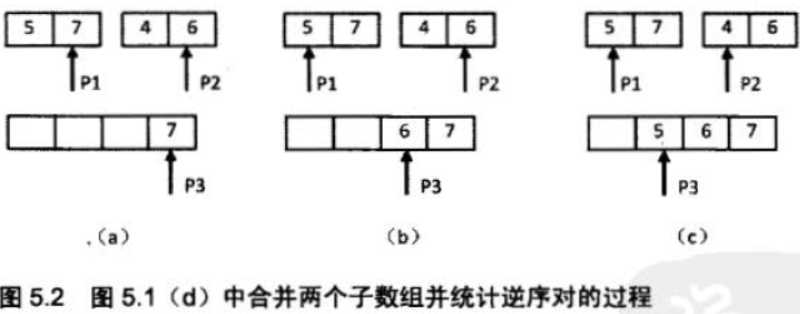

　　先把数组分割成子数组，先统计出子数组内部的逆序对的数目，然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中，还需要对数组进行排序。如果对排序算法很熟悉，我们不难发现这个过程实际上就是归并排序。

#include <iostream>
#include <vector>
using namespace std;

class Solution
{
    public:
        int inverse_pair(vector<int> &data);
        long long inverse_pair_core(vector<int> &data,vector<int> &cp,int start,int end);
};
int Solution::inverse_pair(vector<int> &data)
{
    if(data.empty()||data.size()<=0)
        return -1;
    vector<int> cp(data.begin(),data.end());
    
    return inverse_pair_core(data,cp,0,data.size()-1)%1000000007;
}
long long Solution::inverse_pair_core(vector<int> &data,vector<int> &cp,int start,int end)
{
    if(start==end)//划分数组，子数组只有一个元素时的情况 
    {
        cp[start]=data[start];
        return 0;
    }
    
    int mid=(start+end)/2;
    long long left_count=inverse_pair_core(cp,data,start,mid);
    long long right_count=inverse_pair_core(cp,data,mid+1,end);
    int i=mid;
    int j=end;
    int cp_index=end;
    int count=0;
    
    while(i>=start&&j>mid)
    {
        if(data[i]>data[j])
        {
            cp[cp_index--]=data[i--];
            count+=j-mid;
        }
        else
            cp[cp_index--]=data[j--];
    }
    while(i>=start)
        cp[cp_index--]=data[i--];
    while(j>mid)
        cp[cp_index--]=data[j--];
    
    return left_count+right_count+count;
}
int main()
{
    vector<int> data{7,5,6,4};
    Solution s;
    cout<<s.inverse_pair(data)<<endl;
    return 0;
}