Geatpy遗传算法在曲线寻优上的初步探究

Posted 2021-02-07 dent-lu

园子里关于遗传算法的教案不少，但基于geatpy框架的并未多见，故分享此文以作参考，还望广大园友多多指教！

Geatpy出自三所名校联合团队之手，是遗传算法领域的权威框架（python），其效率之高、应用领域之广远胜诸多第三方工具，此处不作赘述，直接上链接：

官网：http://www.geatpy.com/start

源码：https://github.com/geatpy-dev/geatpy/tree/master/geatpy

使用Geatpy需要安装geatpy模块（pip install geatpy），linux下如果装完后import时出现报错，可以下载我帖尾链接里的wheel文件进行安装。

言归正传，根据经典的遗传算法流程，无外乎这几个步骤：种群初始化 ->（适应度评价 -> 遴选 -> 交叉 -> 变异）<- 循环进化直至终止条件达标。

当然，有关遗传算法的原理和过程不做深讨，本文旨在剖析遗传算法在阵曲线寻优上的高效应用，我写了一个简单示例来帮助大家更好的理解，代码如下：

---

# -*- coding: utf-8 -*-
"""punishing.py - 罚函数demo"""

import numpy as np

def punishing(LegV, FitnV):
    FitnV[np.where(LegV == 0)[0]] = 0
    return FitnV

---

# -*- coding: utf-8 -*-
""" aimfc.py即目标函数，本例通过输入每一代的染色体，由自定义评价函数计算与目标曲线的面积差，作为目标函数值ObjV来输出 """

import numpy as np

def MakeObjCurve(width):
    ‘‘‘ 创建目标曲线，此处定义为一组正弦波拼接序列 ‘‘‘
    n1 = width//3
    n2 = width - 2*n1
    x1=np.cos(np.arange(0,n1)) * 1
    x2=np.cos(np.arange(0,n1)) * 4
    x3=np.cos(np.arange(0,n2)) * 2
    ObjCurve=np.hstack((x1,x2,x3))
    return ObjCurve

def CalScore(chrom):
    ‘‘‘ 返回染色体与目标曲线之间的面积的倒数作为评分值 ‘‘‘
    objCurve = MakeObjCurve(len(chrom))
    area = chrom - objCurve
    area *= 10**5                   #调整系数确保分值不受小数项干扰
    score = 1 / np.dot(area, area)  #计算差值的平方和以简化求面积过程
    return score

def myEvaFunc(chroms):
    ‘‘‘ 自定义评价函数，以评分值作为目标函数值 ‘‘‘
    scores = []
    for chrom in chroms:
        score = CalScore(chrom)
        scores.append(score)
    scores = np.array([scores]).T
    return scores

def aimfuc(Phen, LegV):

    ObjV = myEvaFunc(Phen)
    exIdx = np.argmin(ObjV[:, 0])

    # 惩罚方法2： 标记非可行解在可行性列向量中对应的值为0，并编写punishing罚函数来修改非可行解的适应度。
    # 也可以不写punishing，因为Geatpy内置的算法模板及内核已经对LegV标记为0的个体的适应度作出了修改。
    # 使用punishing罚函数实质上是对非可行解个体的适应度作进一步的修改
    LegV[exIdx] = 0 # 对非可行解作出标记，使其在可行性列向量中对应的值为0，此处标记的是得分最小项

    return [ObjV, LegV]

---

# -*- coding: utf-8 -*-
""" main.py即主函数，本例仅用于演示“已知曲线寻优”的过程 """

import numpy as np
import geatpy as ga
import time
import matplotlib.pyplot as plt

def search_objects(directory):
    directory=os.path.normpath(directory)  #规格化，防止分隔符造成的差异
    if not os.path.isdir(directory):
        raise IOError("The directory ‘"+"‘ doesn‘t exist!")
    objects={}
    for curdir,substrs,files in os.walk(directory):
        for jpeg in (file for file in files if file.endswith(‘.csv‘)):
            path=os.path.join(curdir,jpeg)
            label=path.split(os.path.sep)[-2]
            if label not in objects:
                objects[label]=[]
            objects[label].append(path)
    return objects

def sga_mps_real_templet(AIM_M, AIM_F, PUN_M, PUN_F, FieldDRs, problem, maxormin, MAXGEN, NIND, SUBPOP, GGAP, selectStyle, recombinStyle, recopt, pm, distribute, drawing = 1):
    """ 基于多种群独立进化单目标编程模板(实值编码)，各种群独立将父子两代合并进行选择，采取精英保留机制 """

    #==========================初始化配置===========================
    GGAP = 0.5 # 因为父子合并后选择，因此要将代沟设为0.5以维持种群规模
    # 获取目标函数和罚函数
    aimfuc = getattr(AIM_M, AIM_F) # 获得目标函数
    if PUN_F is not None:
        punishing = getattr(PUN_M, PUN_F) # 获得罚函数
    NVAR = FieldDRs[0].shape[1] # 得到控制变量的个数
    # 定义全局进化记录器，初始值为nan
    pop_trace = (np.zeros((MAXGEN ,2)) * np.nan)
    pop_trace[:, 0] = 0
    # 定义变量记录器，记录控制变量值，初始值为nan
    var_trace = (np.zeros((MAXGEN ,NVAR)) * np.nan)
    """=========================开始遗传算法进化======================="""
    start_time = time.time() # 开始计时
    # 对于各个网格分别进行进化，采用全局进化记录器记录最优值
    for index in range(len(FieldDRs)): # 遍历各个子种群，各子种群独立进化，互相不竞争
        FieldDR = FieldDRs[index]
        if problem == ‘R‘:
            Chrom = ga.crtrp(NIND, FieldDR) # 生成初始种群
        elif problem == ‘I‘:
            Chrom = ga.crtip(NIND, FieldDR)
        LegV = np.ones((NIND, 1)) # 初始化种群的可行性列向量
        [ObjV, LegV] = aimfuc(Chrom, LegV) # 求初始种群的目标函数值
        repnum = 0 # 初始化重复个体数为0
        ax = None # 存储上一帧图形
        gen = 0
        badCounter = 0 # 用于记录在“遗忘策略下”被忽略的代数
        # 开始进化！！
        while gen < MAXGEN:
            if badCounter >= 10 * MAXGEN: # 若多花了10倍的迭代次数仍没有可行解出现，则跳出
                break
            # 进行遗传算子，生成子代
            SelCh = ga.recombin(recombinStyle, Chrom, recopt, SUBPOP) # 重组
            if problem == ‘R‘:
                SelCh = ga.mutbga(SelCh,FieldDR, pm) # 变异
                if repnum > Chrom.shape[0] * 0.01: # 当最优个体重复率高达1%时，进行一次高斯变异
                    SelCh = ga.mutgau(SelCh, FieldDR, pm) # 高斯变异
            elif problem == ‘I‘:
                SelCh = ga.mutint(SelCh, FieldDR, pm)
            LegVSel = np.ones((SelCh.shape[0], 1)) # 初始化育种种群的可行性列向量
            [ObjVSel, LegVSel] = aimfuc(SelCh, LegVSel) # 求育种种群的目标函数值
            # 父子合并
            Chrom = np.vstack([Chrom, SelCh])
            ObjV = np.vstack([ObjV, ObjVSel])
            LegV = np.vstack([LegV, LegVSel])
            FitnV = ga.ranking(maxormin * ObjV, LegV, None, SUBPOP) # 适应度评价
            if PUN_F is not None:
                FitnV = punishing(LegV, FitnV) # 调用惩罚函数
            repnum = len(np.where(ObjV[np.argmax(FitnV)] == ObjV)[0]) # 计算最优个体重复数
            # 记录进化过程
            bestIdx = np.argmax(FitnV)
            if (LegV[bestIdx] != 0) and ((np.isnan(pop_trace[gen,1])) or ((maxormin == 1) & (pop_trace[gen,1] >= ObjV[bestIdx])) or ((maxormin == -1) & (pop_trace[gen,1] <= ObjV[bestIdx]))):
                feasible = np.where(LegV != 0)[0] # 排除非可行解
                pop_trace[gen,0] += np.sum(ObjV[feasible]) / ObjV[feasible].shape[0] / len(FieldDRs) # 记录种群个体平均目标函数值
                pop_trace[gen,1] = ObjV[bestIdx] # 记录当代目标函数的最优值
                var_trace[gen,:] = Chrom[bestIdx, :] # 记录当代最优的控制变量值
                # 绘制动态图
                if drawing == 2:
                    ax = ga.sgaplot(pop_trace[:,[1]],‘子种群‘+str(index+1)+‘各代种群最优个体目标函数值‘, False, ax, gen)
                badCounter = 0 # badCounter计数器清零
            else:
                gen -= 1 # 忽略这一代（遗忘策略）
                badCounter += 1
            if distribute == True: # 若要增强种群的分布性（可能会造成收敛慢）
                idx = np.argsort(ObjV[:, 0], 0)
                dis = np.diff(ObjV[idx,0]) / (np.max(ObjV[idx,0]) - np.min(ObjV[idx,0]) + 1)# 差分计算距离的修正偏移量
                dis = np.hstack([dis, dis[-1]])
                dis = dis + np.min(dis) # 修正偏移量+最小量=修正绝对量
                FitnV[idx, 0] *= np.exp(dis) # 根据相邻距离修改适应度，突出相邻距离大的个体，以增加种群的多样性
            [Chrom, ObjV, LegV] = ga.selecting(selectStyle, Chrom, FitnV, GGAP, SUBPOP, ObjV, LegV) # 选择
            gen += 1
    end_time = time.time() # 结束计时
    times = end_time - start_time
    # 后处理进化记录器
    delIdx = np.where(np.isnan(pop_trace))[0]
    pop_trace = np.delete(pop_trace, delIdx, 0)
    var_trace = np.delete(var_trace, delIdx, 0)
    if pop_trace.shape[0] == 0:
        raise RuntimeError(‘error: no feasible solution. (有效进化代数为0，没找到可行解。)‘)
    # 输出结果
    if maxormin == 1:
        best_gen = np.argmin(pop_trace[:, 1]) # 记录最优种群是在哪一代
        best_ObjV = np.min(pop_trace[:, 1])
    elif maxormin == -1:
        best_gen = np.argmax(pop_trace[:, 1]) # 记录最优种群是在哪一代
        best_ObjV = np.max(pop_trace[:, 1])
    print(‘最优的目标函数值为：%s‘%(best_ObjV))
    print(‘最优的控制变量值为：‘)
    for i in range(NVAR):
        print(var_trace[best_gen, i])
    print(‘有效进化代数：%s‘%(pop_trace.shape[0]))
    print(‘最优的一代是第 %s 代‘%(best_gen + 1))
    print(‘时间已过 %s 秒‘%(times))
    # 绘图
    if drawing != 0:
        ga.trcplot(pop_trace, [[‘种群个体平均目标函数值‘, ‘种群最优个体目标函数值‘]])
    # 返回进化记录器、变量记录器以及执行时间
    return [pop_trace, var_trace, times, best_gen]

# 获取函数接口地址
AIM_M = __import__(‘aimfuc‘)
PUN_M = __import__(‘punishing‘)
POP_SIZE = 300          # 种群高度
CHROM_LENGTH = 20       # 染色体宽度
max_generation = 150    # 进化代数
chrom_bottom = -4       #染色体数值下限
chrom_top = 4           #染色体数值上限

# 变量设置
x = []; b = []
for i in range(CHROM_LENGTH):
    x.append([chrom_bottom, chrom_top]) # 自变量的范围
    b.append([0, 0]) # 自变量是否包含下界
ranges=np.vstack(x).T # 生成自变量的范围矩阵
borders = np.vstack(b).T # 生成自变量的边界矩阵
precisions = [1]*CHROM_LENGTH # 在二进制/格雷码编码中代表自变量的编码精度，当控制变量是连续型时，根据crtfld参考资料，该变量只表示边界精度，故设置为一定的正数即可
# 生成网格化后的区域描述器集合
FieldDRs = []
for i in range(1):
    FieldDRs.append(ga.crtfld(ranges, borders, precisions))

# 调用编程模板(设置problem = ‘R‘处理实数型变量问题，详见该算法模板的源代码)
[pop_trace, var_trace, times, best_gen] = sga_mps_real_templet(AIM_M, ‘aimfuc‘, PUN_M, ‘punishing‘,
 FieldDRs, problem = ‘R‘, maxormin = -1, MAXGEN = max_generation, NIND = POP_SIZE, SUBPOP = 1, GGAP = 0.9,  selectStyle = ‘tour‘, recombinStyle = ‘xovdprs‘, recopt = 0.9, pm = 0.3, distribute = True, drawing = 1)

bstChrom = var_trace[best_gen]
objCurve = AIM_M.MakeObjCurve(CHROM_LENGTH)

plt.ion()
fig = plt.figure(‘曲线寻优演示‘,facecolor=‘lightgray‘)
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.set_title("Evaluation Map")
ax1.grid(axis=‘y‘, linestyle=‘:‘)
for i in range(max_generation):
    if i%5==0:
        ax1.plot(var_trace[i], ‘o-‘)
        ax2.cla()
        ax2.set_title("最优染色体[gen:%i]"%(i+1))
        ax2.plot(var_trace[i], ‘o-‘, c=‘dodgerblue‘)
        plt.pause(0.001)
ax2.cla()
ax2.grid(axis=‘y‘, linestyle=‘:‘)
ax2.plot(objCurve, ‘o-‘, c=‘orangered‘, label=‘目标曲线‘)
ax2.plot(bstChrom, ‘o-‘, c=‘dodgerblue‘, label=‘最优染色体[gen:%i]‘%(best_gen+1))
plt.legend()
plt.ioff()
plt.show()

请注意，此处我已将模板函数单独放到主函数中以便大家更好的理解，返回值中增加了最优代数以便后续图例的显示。

本例采用的进化模板是sga_mps_real_templet，基于多种群进化单目标（实数值），用于实现寻找目标曲线。

目标曲线的定义函数在aimfc.py的MakeObjCurve函数中，本例为3段振幅不同的cos函数拼接而成的模拟曲线，宽度20。

种群初始值设置：种群高度300、染色体宽度20（与目标曲线宽度保持一致）、进化代数150、染色体数值上下限[-4,4]（与目标曲线的上下限保持一致）。

接着我们开始寻优，通过CalScore函数计算每代种群的每条染色体与目标函数之间的差值，经过一定的系数转换得到评分值（差值越大，评分越低），以单目标（1列）形式输出，由geatpy的ranking函数来决定适应度评价，然后继续遴选、交叉、变异，如此循环往复，直至达到近似目标值时终止（本例设定为150代时终止），寻优过程如下图：

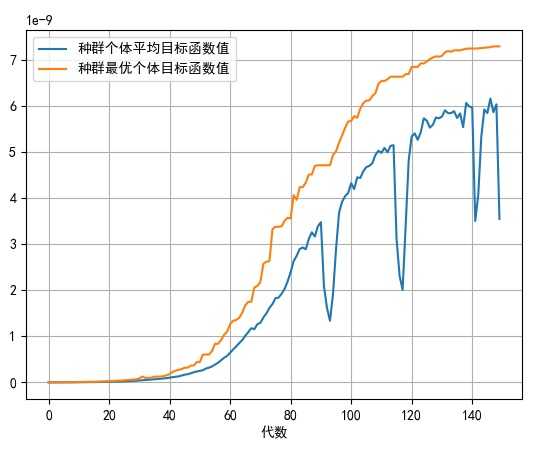
最优的目标函数值为：7.287567405118076e-09
有效进化代数：150
最优的一代是第 148 代
时间已过 1.3259999752044678 秒

可以看到从50代左右优化曲线开始显著上扬，直到130代左右逐渐平缓，并且耗时非常少，来看寻优结果图：

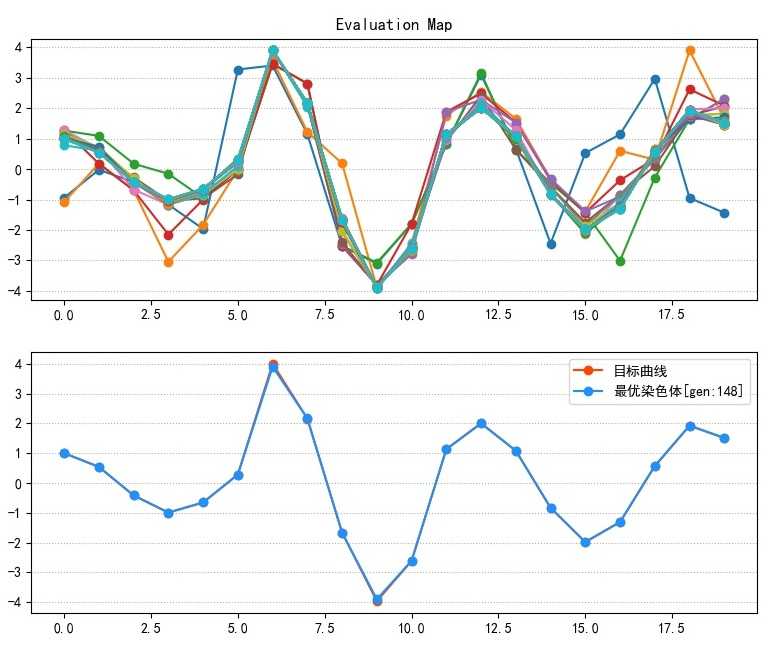
可以看到除了第6个点的数值有细微差异之外，其他点几乎都是吻合的，基本实现了目标曲线的寻求。

之所以抛出本例，最重要的一点在于geatpy遗传算法不仅能寻求已知的目标函数，还可以通过自定义的评分体系或第三方接口来参与实现寻优过程，只需将CalScore函数稍作改动即可，以上。

【wheel文件】: https://pan.baidu.com/s/1BwLq_m3Dd5RMqatvTYXrAw 提取码: vgkz