RAY TRACING THE REST OF YOUR LIFE 超详解 光线追踪 3-1
Posted lv-anchoret
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了RAY TRACING THE REST OF YOUR LIFE 超详解 光线追踪 3-1相关的知识,希望对你有一定的参考价值。
今天起,我们就开始学习第三本书了

这本书主要讲的是蒙特卡罗渲染,以及相关的数学、术语概念等
我们先来一个简单的开胃菜
chapter 1:A Simple Monte Carlo Program
蒙特卡罗方法(MC)是一种统计模拟方法,是一类很重要的数值计算方法,它是一种使用随机数解决好很多实际问题的方法。
先来看一个很简单的例子:估计π
有很多经典的方法,其中之一是
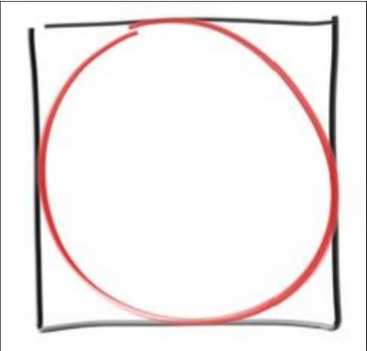
假设你扔了很多随机的点到方框中,那么有一部分在圆内,其中圆内点和方框点的比例应该就是圆的面积和方框面积的比例,由此:
比例 = (π * R * R)/((2R)*(2R)) = π/4
所以上式和R无关,我们任意取R = 1,圆心位于原点,则
#include <iostream> #include <lvgm andfunc.hpp> #define stds std:: using namespace lvgm; void estimate_π(const size_t points) { int inside = 0; for (int i = 0; i < points; ++i) { double x = 2 * rand01() - 1; double y = 2 * rand01() - 1; if (x*x + y*y < 1) inside++; } stds cout << "Estimate of π by" << points << "test points is " << 4 * double(inside) / points << stds endl; }
int main()
{
estimate_π(1000);
estimate_π(10000);
estimate_π(100000);
estimate_π(1000000);
estimate_π(10000000);
estimate_π(10000000 / 2);
}
模拟结果为
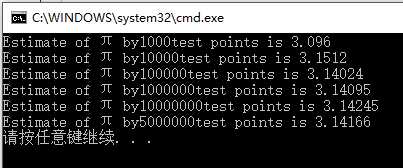
当然我们可以利用下面的程序使结果迅速逼近π
void lawDiminishingReturns() { int inside = 0; int runs = 0; while (true) { runs++; double x = 2 * rand01() - 1; double y = 2 * rand01() - 1; if (x*x + y*y < 1) inside++; if(runs % 10000 == 0) stds cout << "Estimate of π by" << runs << "test points is " << 4 * double(inside) / runs << stds endl; } }
结果:
.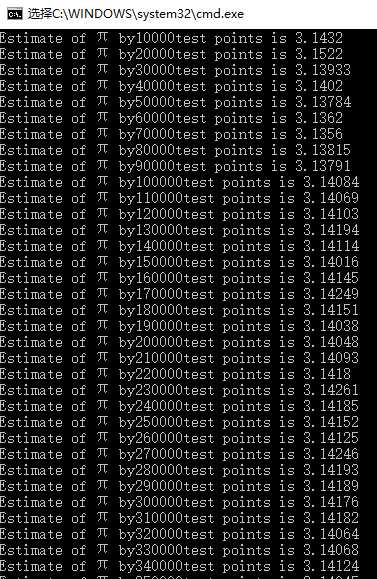
一开始非常快速的逼近π,之后变化就比较缓慢了,这是一个收益递减法(Law of Diminishing Returns)的例子
即每一个样本对结果的收益少于后面一个,这个是MC的一个缺点,我们可以通过对样本进行分层来减轻这种递减收益,此法通常称为抖动
我们进行网格划分,并在每个网格中选取一个样本:
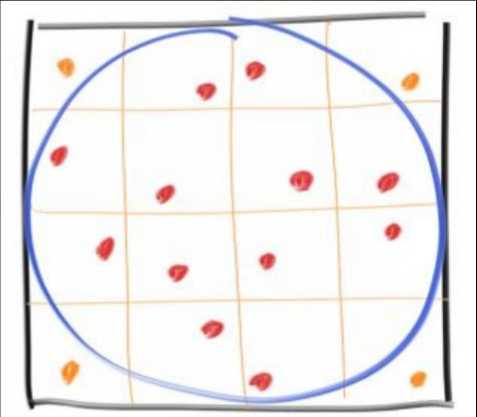
我们采用边长为1e4的方框进行测试
void stratify() { size_t inside{ 0 }; size_t circle_stratified{ 0 }; size_t sqrtAll = 1e4; for (int i = 0; i < sqrtAll; ++i) for (int j = 0; j < sqrtAll; ++j) { double x = 2 * rand01() - 1; double y = 2 * rand01() - 1; if (x*x + y*y < 1) inside++; x = 2 * ((i + rand01()) / sqrtAll) - 1; y = 2 * ((j + rand01()) / sqrtAll) - 1; if (x*x + y*y < 1) circle_stratified++; } stds cout << "Regular Estimate of π by 1e8 test points is " << 4 * double(inside) / 1e8 << stds endl; stds cout << "Stratified Estimate of π by 1e8 test points is " << 4 * double(circle_stratified) / 1e8 << stds endl; }
图片渲染运算读写文件的时候慢。。如今控制台运算输出也整不动了。。。。
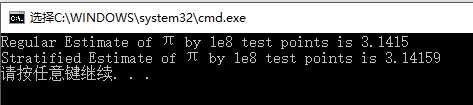
有意思~
分层方法能更好地收敛于渐近率。不足之处是,这个优势随着问题的维度而降低(例如,对于3D球体积版本,差距会更小)。 这被称为维度诅咒(=.=)。 我们的工程将是非常高的维度(每个反射增加两个维度),所以我不会在本书中进行分层。
但是,如果你做的是单反射或阴影或某些严格的2D问题,分层是个很好的选择
感谢您的阅读,生活愉快~
以上是关于RAY TRACING THE REST OF YOUR LIFE 超详解 光线追踪 3-1的主要内容,如果未能解决你的问题,请参考以下文章
RAY TRACING THE REST OF YOUR LIFE 超详解 光线追踪 3-3 蒙特卡罗
RAY TRACING THE REST OF YOUR LIFE 超详解 光线追踪 3-5 random direction & ONB
Ray Tracing The Next Week 超详解 光线追踪2-9
Ray Tracing The Next Week 超详解 光线追踪2-6 Cornell box