GF(p)上的ELGamal型椭圆曲线密码详解(Java实现)
Posted mx-lqk
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了GF(p)上的ELGamal型椭圆曲线密码详解(Java实现)相关的知识,希望对你有一定的参考价值。
椭圆曲线密码
椭圆曲线密码(Elliptic Curve Cryptosystem),简称ECC,是Neal Koblitz和Victor Miller于1985年提出的。
研究发现,有限域上的椭圆曲线上的一些点构成交换群,而且离散对数问题是难解的。于是在此群上定义ELGamal密码,并称为椭圆曲线密码。
目前,椭圆曲线密码已成为除RSA密码之外呼声最高的公钥密码之一。它密钥短、签名短、软件实现规模小、硬件实现电路省电。普遍认为,160位长的椭圆曲线密码的安全性相当于1024位的RSA密码,而且运算速度也较快。
GF(p)上的椭圆曲线
设p是大于3的素数,且4a3+27b2≠0(mod p),称曲线
y2=x3+ax+b(a,b∈GF(p))
为GF(p)上的椭圆曲线。
由椭圆曲线方程可得到一同余方程:
y2=x3+ax+b(mod p)(a,b∈GF(p))
其解为一个二元组(x,y),其中x,y∈GF(p),表示椭圆曲线上的一个点,称为该椭圆曲线上的解点。
无穷点O
定义一个点O(∞,∞)表示无穷点,作为0元素。
两解点相加
设P(x1,y1)和Q(x2,y2)是解点,R(x3,y3)=P(x1,y1)+Q(x2,y2):
1.若P为无穷点,即P=O,此时R=P+Q=Q;若Q为无穷点,即Q=O,此时R=P+Q=P;若P和Q都为无穷点,即P=Q=O,则R=P+Q=O。
2.若x1=x2且y1=y2,即P=Q,此时R=P+Q=2P,其中
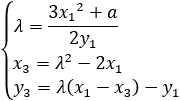
3.若x1=x2而y1=-y2,此时称Q点为P点的逆,记为P=-Q,且R=P+Q=O。
4.除上述特殊情况之外的一般情况,即P≠±Q时,R=P+Q,其中
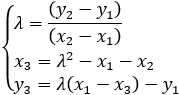
集合E={所有的解点,无穷点O}和加法运算构成加法交换群。设G(G≠O,即G为一个解点)为一个加法群的生成元,则使得nG=G+G+...+G=O的倍数n为该加法群的阶。加法群的阶整除集合E的阶,即n | |E|。
求椭圆曲线的所有解点
当p较小,即GF(p)较小时,可以利用穷举的方法根据同余方程y2=x3+ax+b(mod p)(a,b∈GF(p))求出所有解点。
具体方法为:求出x取0~p-1,x3+ax+b(mod p)的结果是否为模p的二次剩余。如果是,则一个x值可得到两个对应的y值,也就得到互逆的两个解点。
e.m.取p=11,椭圆曲线y2=x3+x+6
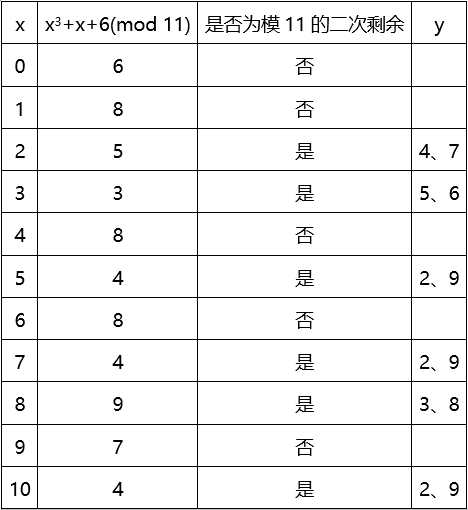
由此表得到所有的解点:(2,4)、(2,7)、(3,5)、(3,6)、(5,2)、(5,9)、(7,2)、(7,9)、(8,3)、(8,8)、(10,2)、(10,9),再加上无穷点O共13个点的集合E加上加法运算就构成一个加法交换群。
因为集合E的阶|E|=13为素数,所以该加法群的阶为13。
取G=(2,7)为生成元,
G=(2,7),2G=(5,2),
3G=(8,3),4G=(10,2),
5G=(3,6),6G=(7,9),
7G=(7,2),8G=(3,5),
9G=(10,9),10G=(8,8),
11G=(5,9),12G=(2,4),
最终得到13G=O,所以加法群的阶为13。
ELGamal型椭圆曲线密码
1.选择一个素数p,从而确定有限域GF(p),将p公开。
2.选择元素a,b∈GF(p),从而确定一条GF(p)上的椭圆曲线,确定加法交换群E,将a和b公开。
3.选择一个大素数n,并确定一个阶为n的基点G(x,y),将n和G(x,y)公开。
4.余因子h=|E|/n,将h公开。
5.随机选择一个整数d(0<d<n)作为私钥保密。
6.定义Q=dG作为公钥公开。
加密
1.随机选择一个整数k(0<k<n)。
2.计算X1=kG。
3.计算X2=kQ,若x2=∞,则回到第1步。
4.加密:C=Mx2(mod n)。
5.将(X1,C)作为密文发送。
解密
1.用私钥d求出X2=dX1。
2.解密:M=Cx2-1(mod n)。
推荐椭圆曲线
NIST向社会推荐了5条素域GF(p)上随机选取的椭圆曲线:
P-192
p=2192-264-1
a=-3
b=64210519 E59C80E7 0FA7E9AB 72243049 FEB8DEEC C146B9B1
x=188DA80E B03090F6 7CBf20EB 43A18800 F4FF0AFD 82FF1012
y=07192B95 FFC8DA78 631011ED 6B24CDD5 73F977A1 1E794811
n=FFFFFFFF FFFFFFFF FFFFFFFF 99DEF836 146BC9B1 B4D22831
h=1
P-224
p=2224-296-1
a=-3
b=B4050A85 0C04B3AB F5413256 5044B0B7 D7BFD8BA 270B3943 2355FFB4
x=B70E0CBD 6BB4BF7F 321390B9 4A03C1D3 56C21122 343280D6 115C1D21
y=BD376388 B5F723FB 4C22DFE6 CD4375A0 5A074764 44D58199 85007E34
n=FFFFFFFF FFFFFFFF FFFFFFFF FFFF16A2 E0B8F03E 13DD2945 5C5C2A3D
h=1
P-256
p=2256-2224+2192+296-1
a=-3
b=5AC635D8 AA3A93E7 B3EBBD55 769886BC 651D06B0 CC53B0F6 3BCE3C3E 27D2604B
x=6B17D1F2 E12C4247 F8BCE6E5 63A440F2 77037D81 2DEB33A0 F4A13945 D898C296
y=4FE342E2 FE1A7F9B 8EE7EB4A 7C0F9E16 2BCE3357 6B315ECE CBB64068 37BF51F5
n=FFFFFFFF 00000000 FFFFFFFF FFFFFFFF BCE6FAAD A7179E84 F3B9CAC2 FC632551
h=1
P-384
p=2384-2128-296+232-1
a=-3
b=B3312FA7 E23EE7E4 988E056B E3F82D19 181D9C6E FE814112 0314088F 5013875A C656398D 8A2ED19D 2A85C8ED D3EC2AEF
x=AA87CA22 BE8B0537 8EB1C71E F320AD74 6E1D3B62 8BA79B98 59F741E0 82542A38 5502F25D BF55296C 3A545E38 72760AB7
y=3617DE4A 96262C6F 5D9E98BF 9292DC29 F8F41DBD 289A147C E9DA3113 B5F0B8C0 0A60B1CE 1D7E819D 7A431D7C 90EA0E5F
n=FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF C7634D81 F4372DDF 581A0DB2 48B0A77A ECEC196A CCC52973
h=1
P-521
p=2521-1
a=-3
b=00000051 953EB961 8E1C9A1F 929A21A0 B68540EE A2DA725B 99B315F3 B8B48991 8EF109E1 56193951 EC7E937B 1652C0BD 3BB1BF07 3573DF88 3D2C34F1 EF451FD4 6B503F00
x=000000C6 858E06B7 0404E9CD 9E3ECB66 2395B442 9C648139 053FB521 F828AF60 6B4D3DBA A14B5E77 EFE75928 FE1DC127 A2FFA8DE 3348B3C1 856A429B F97E7E31 C2E5BD66
y=00000118 39296A78 9A3BC004 5C8A5FB4 2C7D1BD9 98F54449 579B4468 17AFBD17 273E662C 97EE7299 5EF42640 C550B901 3FAD0761 353C7086 A272C240 88BE9476 9FD16650
n=000001FF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 51868783 BF2F966B 7FCC0148 F709A5D0 3BB5C9B8 899C47AE BB6FB71E 91386409
h=1
椭圆曲线密码的安全性
椭圆曲线密码的安全性建立在椭圆曲线离散对数问题的困难性之上。当素数p和n足够大时椭圆曲线密码是安全的。这就要求椭圆曲线解点群的阶要有大素数因子的根本原因,在理想情况下群的阶本身就是一个大素数。
为了确保椭圆曲线密码的安全,应当避免使用弱的椭圆曲线。所谓弱的椭圆曲线主要指超奇异椭圆曲线和反常椭圆曲线。
椭圆曲线密码的密钥越长,自然越安全,但是技术实现也就越困难,效率也越低。一般认为,在目前的技术水平下采用190~256位的椭圆曲线,其安全性就足够了。
Java实现
解点类
1 import java.math.BigInteger; 2 3 public class ECPoint { 4 BigInteger x; 5 BigInteger y; 6 7 public ECPoint() { 8 x = null; 9 y = null; 10 } 11 12 public ECPoint(BigInteger x, BigInteger y) { 13 this.x = x; 14 this.y = y; 15 } 16 17 @Override 18 public String toString() { 19 if (isO()) 20 return "O"; 21 return "(" + x.toString(16) + ", " + y.toString(16) + ")"; 22 } 23 24 boolean isO() { 25 if (x == null && y == null) 26 return true; 27 return false; 28 } 29 }
两解点相加
1 /** 2 * 两解点相加 3 * @param p1 4 * @param p2 5 * @return 6 */ 7 ECPoint add(ECPoint p1, ECPoint p2) { 8 if (p1.isO()) return p2; 9 if (p2.isO()) return p1; 10 ECPoint p3 = new ECPoint(); 11 BigInteger lambda; 12 if (p1.x.compareTo(p2.x) == 0) { 13 if (p1.y.compareTo(p2.y) == 0) { 14 lambda = new BigInteger("3").multiply(p1.x.pow(2)).add(a).multiply(new BigInteger("2").multiply(p1.y).modPow(new BigInteger("-1"), p)).mod(p); 15 p3.x = lambda.pow(2).subtract(new BigInteger("2").multiply(p1.x)).mod(p); 16 p3.y = lambda.multiply(p1.x.subtract(p3.x)).subtract(p1.y).mod(p); 17 return p3; 18 } 19 if (p1.y.compareTo(p.subtract(p2.y)) == 0) 20 return p3; 21 } 22 lambda = p2.y.subtract(p1.y).multiply(p2.x.subtract(p1.x).modPow(new BigInteger("-1"), p)).mod(p); 23 p3.x = lambda.pow(2).subtract(p1.x).subtract(p2.x).mod(p); 24 p3.y = lambda.multiply(p1.x.subtract(p3.x)).subtract(p1.y).mod(p); 25 return p3; 26 }
倍乘
1 /** 2 * 倍乘 3 * @param p 4 * @param n 5 * @return np 6 */ 7 ECPoint multiply(ECPoint p, BigInteger n) { 8 ECPoint q = add(p, new ECPoint()); 9 ECPoint r = new ECPoint(); 10 do { 11 if (n.and(new BigInteger("1")).intValue() == 1) 12 r = add(r, q); 13 q = add(q, q); 14 n = n.shiftRight(1); 15 } while (n.intValue() != 0); 16 return r; 17 }
求所有解点
1 /** 2 * 求所有解点 3 * @return 4 */ 5 List<ECPoint> solutionPoints() { 6 List<ECPoint> r = new ArrayList<ECPoint>(); 7 List<BigInteger> l = new ArrayList<BigInteger>(); 8 for (BigInteger y = new BigInteger("1"); y.compareTo(p.divide(new BigInteger("2"))) != 1; y = y.add(new BigInteger("1"))) 9 l.add(y.modPow(new BigInteger("2"), p)); 10 for (BigInteger x = new BigInteger("0"); x.compareTo(p) == -1; x = x.add(new BigInteger("1"))) { 11 BigInteger t = x.pow(3).add(a.multiply(x)).add(b).mod(p); 12 if (isExist(t, l) != -1) { 13 BigInteger y = new BigInteger(isExist(t, l) + ""); 14 r.add(new ECPoint(x, y)); 15 r.add(new ECPoint(x, p.subtract(y))); 16 } 17 } 18 r.add(new ECPoint()); 19 return r; 20 }
1 static int isExist(BigInteger b, List<BigInteger> l) { 2 for (int i = 0; i < l.size(); i++) 3 if (l.get(i).compareTo(b) == 0) return (i + 1); 4 return -1; 5 }
求阶
1 /** 2 * 求阶 3 * @param p 生成元 4 * @return p对应的阶 5 */ 6 BigInteger o(ECPoint p) { 7 BigInteger r = new BigInteger("1"); 8 while (! p.isO()) { 9 r = r.add(new BigInteger("1")); 10 p = multiply(p, r); 11 } 12 return r; 13 }
加密
1 /** 2 * 加密 3 * @param M 4 * @return 5 */ 6 BigInteger[] encrypt(BigInteger M) { 7 BigInteger k; 8 ECPoint X1, X2; 9 do { 10 k = new BigInteger(n.bitLength(), new Random()); 11 } while ((X2 = ec.multiply(Q, k)).x == null); 12 X1 = ec.multiply(G, k); 13 BigInteger[] C = new BigInteger[3]; 14 C[0] = X1.x; 15 C[1] = X1.y; 16 C[2] = M.multiply(X2.x).mod(n); 17 return C; 18 }
解密
1 /** 2 * 解密 3 * @param C 4 * @return 5 */ 6 BigInteger decrypt(BigInteger[] C) { 7 ECPoint X1 = new ECPoint(C[0], C[1]); 8 ECPoint X2 = ec.multiply(X1, d); 9 BigInteger M = C[2].multiply(X2.x.modPow(new BigInteger("-1"), n)).mod(n); 10 return M; 11 }
测试
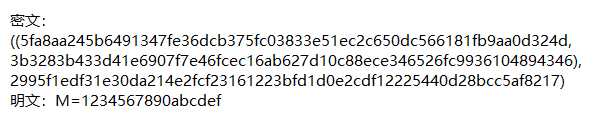
测试数据
M=1234567890abcdef
k=abcdef
测试结果
P-192

P-224

P-256
P-384
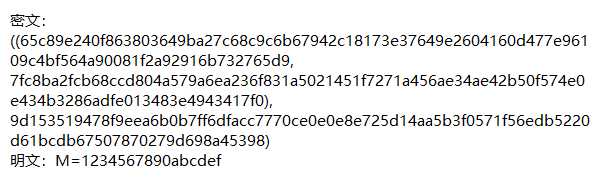
P-521

参考文献
张焕国,唐明.密码学引论(第三版).武汉大学出版社,2015年
以上是关于GF(p)上的ELGamal型椭圆曲线密码详解(Java实现)的主要内容,如果未能解决你的问题,请参考以下文章