实验10-SPSS-自动线性建模

Posted 2021-02-04 xuxaut-558

•  SPSS自动线性建模
• 
  
• 自动线性建模，是在最经常使用的一般线性模型基础上加以改进，让用户输入最少的参数而自动建立线性模型的一个功能。
• 
  
• 刚好市场部提供了一个广告效果预测需求，现在市场部已制定了6月1日至7日广告投放计划，希望通过建立线性
• 回归模型，预测6月1日至7日的购买用户数有多少。我们手中已有1~5月的广告投放效果数据，主要字段有
• “广告费用”、“广告投放渠道数”、“购买用户数”，就以此需求为例，在SPSS中进行自动线性回归分析。
• 1.1-实验步骤：
• (1)SPSS中【分析】-【回归】-【自动线性建模】
• (2)将“购买用户数”变量，从【预测变量(输入)】框移至【目标】框中，将“日期”变量，从【预测变量(输入)】
• 框移至【字段】框中。
• (3)单击【模型选项】卡，勾选【将预测值保存到数据集】复选框。
• 
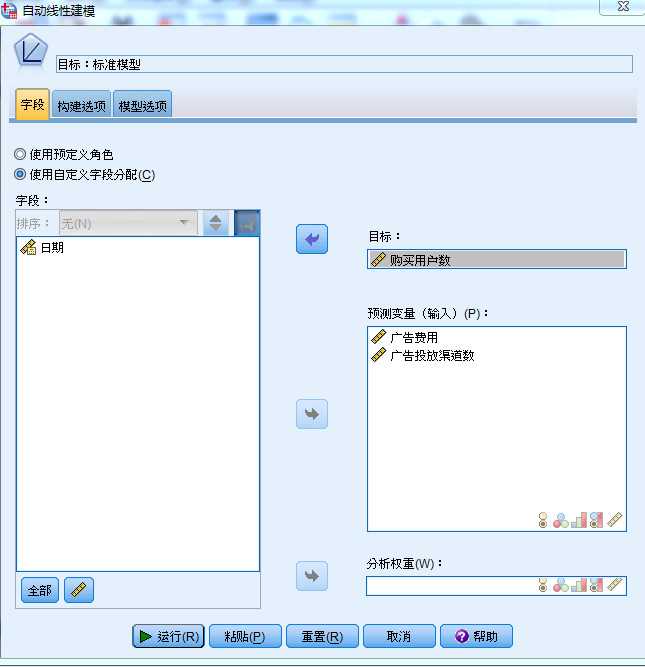                                  图1-1 自动线性建模参数设置
  
• 1.2 模型结果解读
• 现在看看输出结果，和其他SPSS输出结果不同，自动线性回归的结果是以可视化报表方式呈现的。
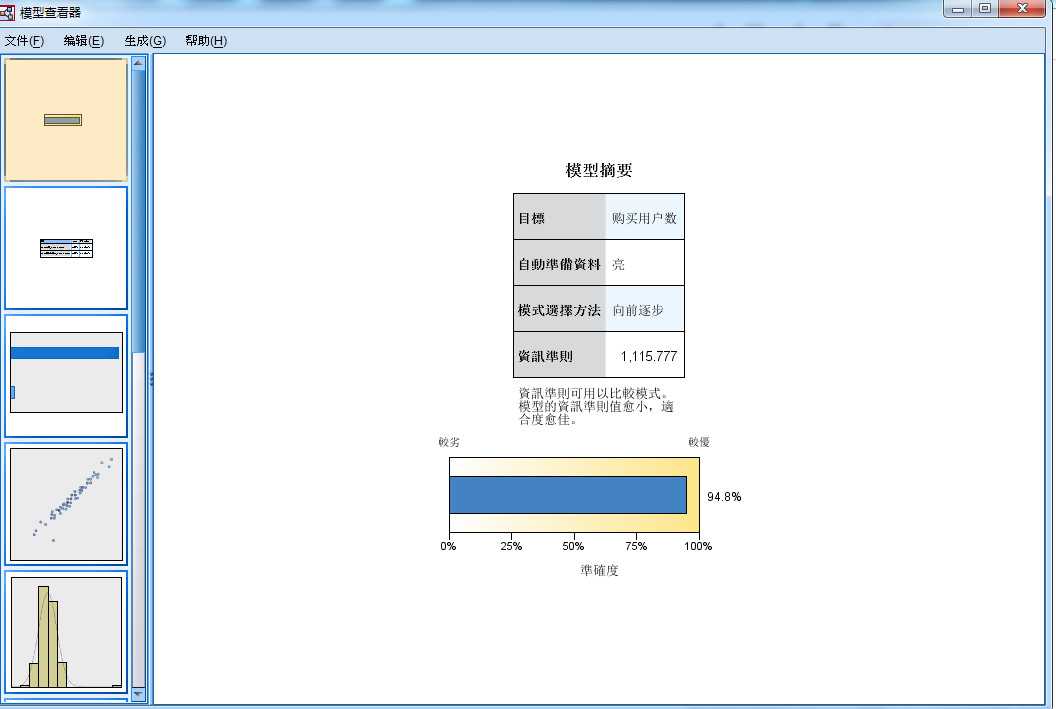
• 2.1 模型摘要 
• 
  
• 
  
  
                                     图 2-1 模型摘要
  
• 
  
• 第一张图为模型摘要，图中用进度条图来展现模型拟合的效果。它类似于普通线性回归中的R^2（决定系数），
• 一般模型准确度大于70%就算拟合不错，60%以下就需要修正模型，可以通过增加或删除一些自变量后再次
• 建模进行修正，这个模型准确度达到了94.8%，效果不错。
• 
  
• 2.2自动准备数据
• 
  
• 
  
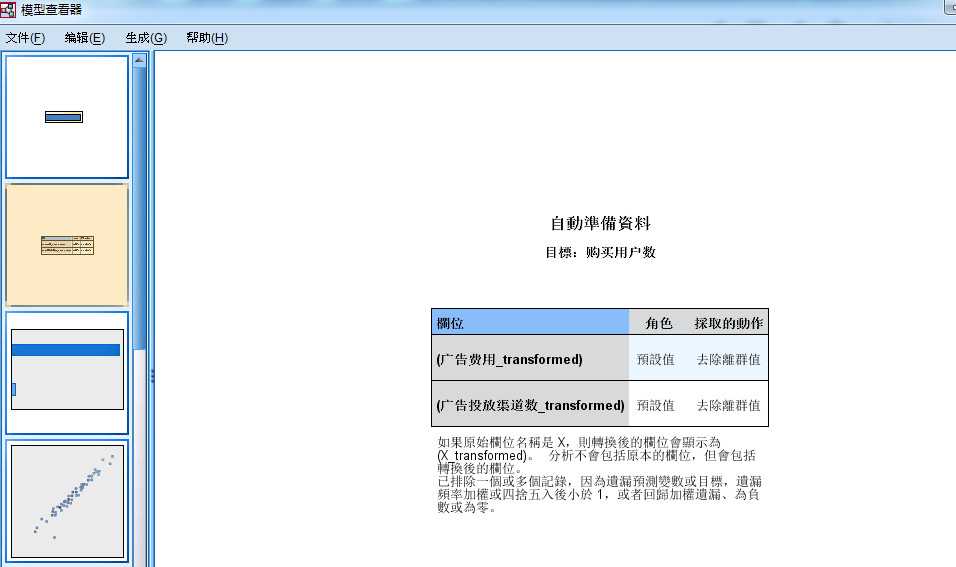
                                       图 2-2
  
• 第二张图是建模的自动准备数据过程信息，比如各个变量的角色，对其进入模型之前都做了哪些处理操作，
• 常见的预处理就是离群值、缺失值等处理，只有勾选【自动准备数据】复选框，SPSS就会自动进行处理。
• 
  
• 2.3 预测变量重要性图
• 
  
• 
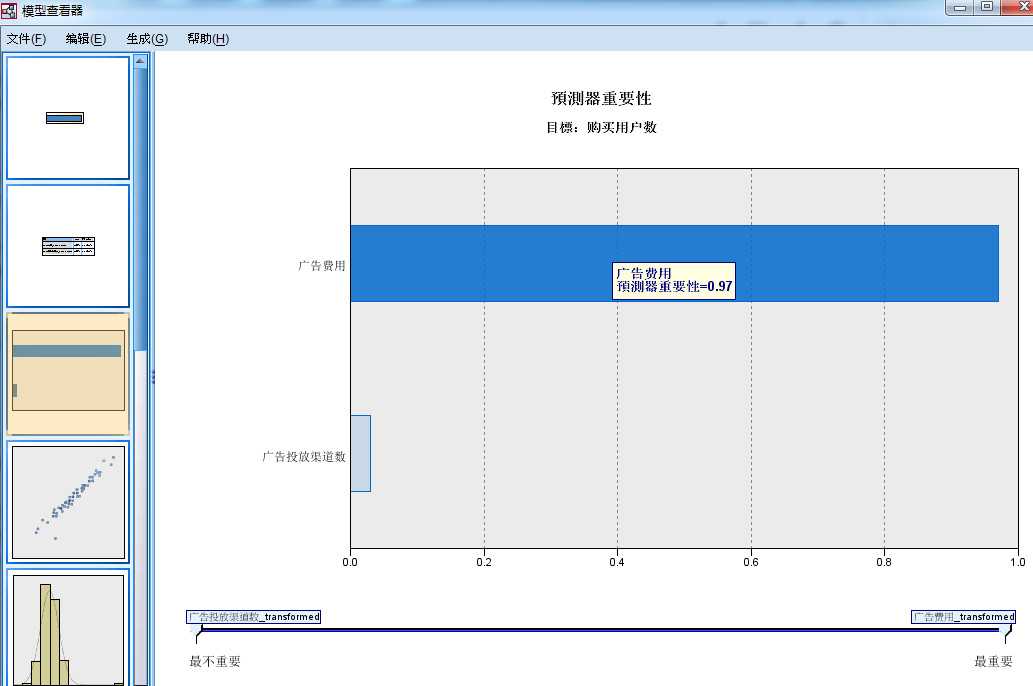
                                      图2-3 预测变量重要性图
  
• 第三张图为预测变量重要性图，如图6-7所示，用条形图的方式给出了模型中每个自变量的重要性，按对
• 因变量影响强度的大小降序排列，重要性是相对值，因此显示的所有自变量的重要性总和为1，其中自变量
• 的重要性与模型精度无关。
• 
  
• 从图中可以看出，“广告费用”变量的重要性最大，而“广告投放渠道数”变量的重要性最小。
• 
  
• 2.4 预测-实测散点图
•                             图2-4 预测-实测散点图
  
• 第四张图为预测-实测散点图，也就是预测值和实际因变量值绘制的散点图，横轴为实际因变量值，
• 纵轴为预测值。它用于考察预测效果，如果效果好，数据点应该是在一条45°线上分布，如图，预测值与实际因变量值较为接近，预测效果好。
• 
  
• 2.5 残差图
  
• 
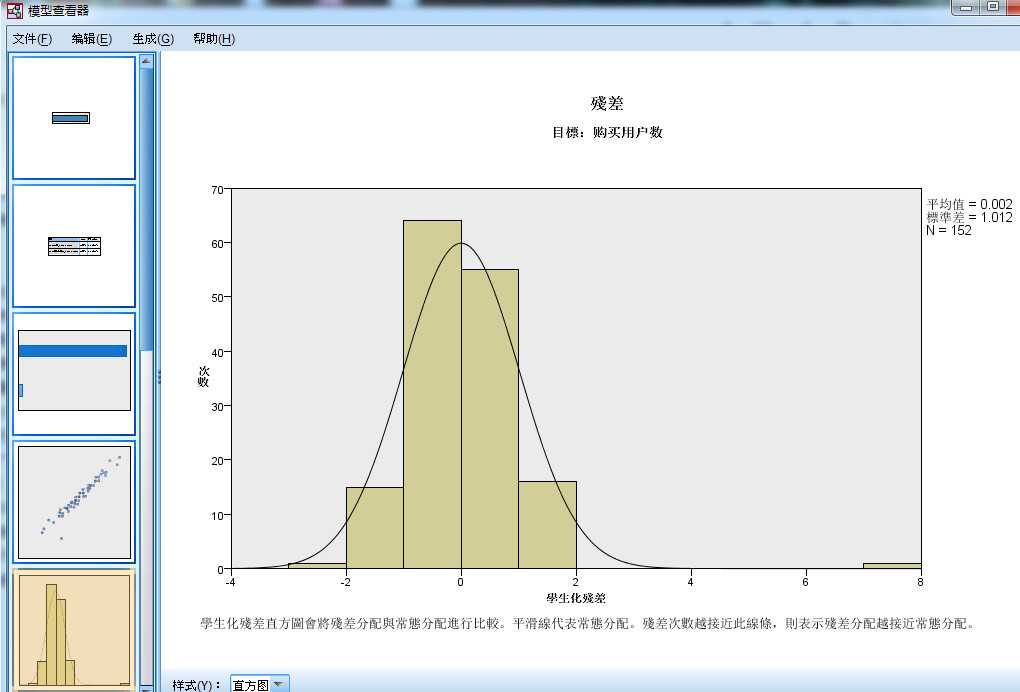
                                 图2-5 残差图
  
• 
  
• 残差是指实际值与预测值之间的差，残差图用于回归诊断，也就是用来判断当前模型是否满足回归模型的假设：
• 回归 模型在理想条件下的残差图是 服从正态分布的，也就是说，图中的残差直方图和正态分布曲线是一致的。
• 如图，残差直方图和正态分布曲线一致，可以得出残差图是接近正态分布的结论，满足回归模型的是假设。
• 
  
• 2.6 离群值
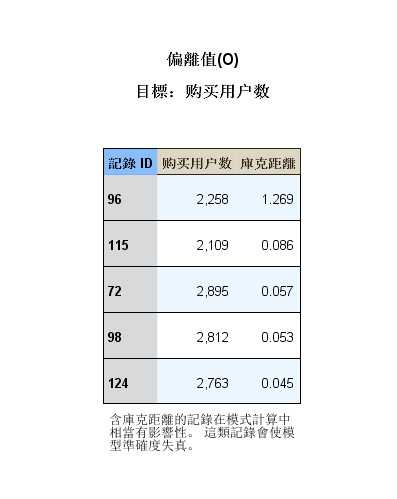•                                 图 2-6 离群值
  
• 第六张图是强影响点(离群值)的诊断，SPSS会计算出库克距离，采用表格的方式输出了强影响点个案ID、因变量及
• 相应的库克距离，库克距离越大的个案对回归拟合影响的程度越大，此类个案可能会导致模型准确度下降。
• 
  
• 2.7 回归效果图
• 
  
  
  
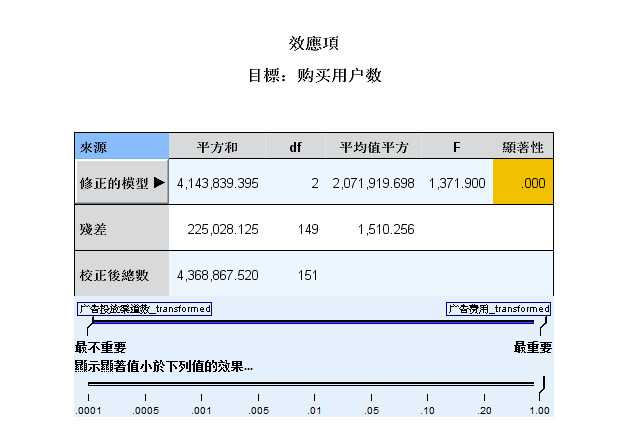                            图 2-7 回归效果图
  
• 第七张图为回归效果图，用于展现及比较各个自变量对因变量的重要性。每个显著的连续变量均会作为一个模型项，
• 并对应一条线条，如果有显著的分类变量纳入模型 ，那么模型将分类变量的每一种显著的类别分别作为一个模型项，
• 并分别对应一条线条。
• 线条上下顺序是按照自变量的重要性大小降序排列的，由此可以判断各个自变量的重要性。
• 线条粗细则表示显著性是水平，显著性水平越高其线条越粗。
• 可以看出，“广告费用”这个自变量对购买用户数的影响最大，重要性为0.97。
• 
  
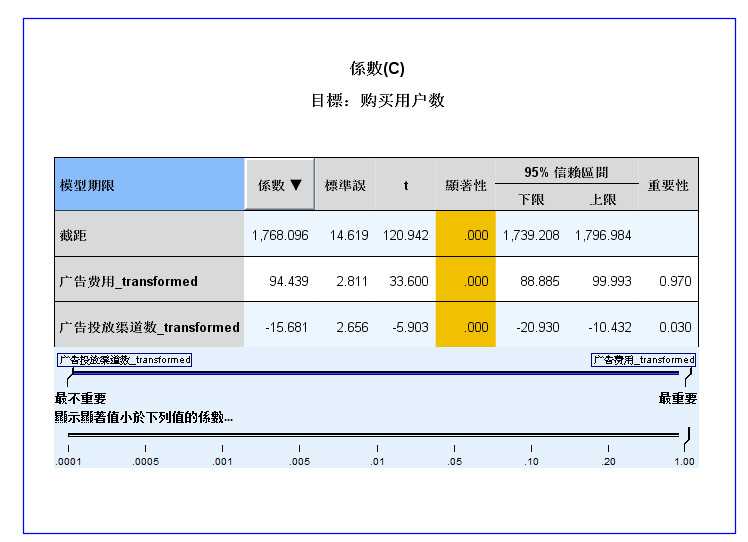
• 2.8 回归系数图
• 
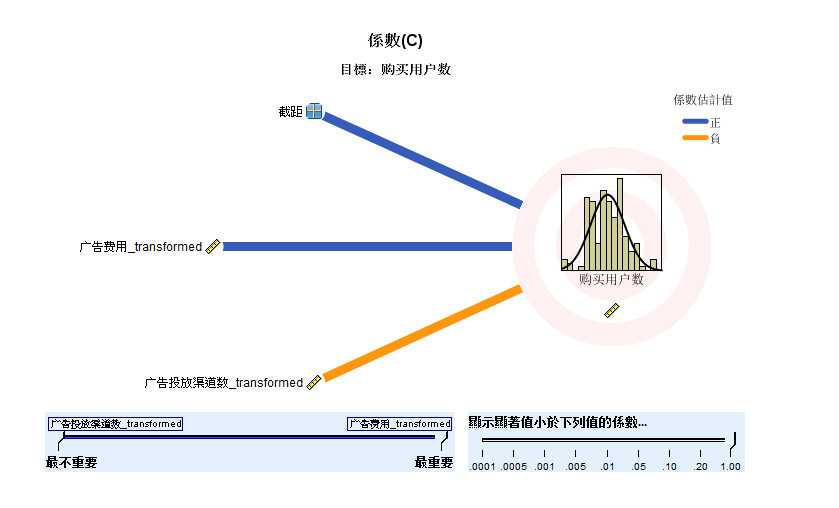
                                 图2-8 回归系数图
  
• 

                                      图2-8 回归系数表
  
• 回归系数图，是这个模型中最重要的一张图，是回归效果图的细化，增加了截距、回归系数等信息，用颜色区分
• 回归系数的正负，蓝色代表正数，橙色代表负数。同样，线条顺序是按照重要性大小降序排列的，线条粗细表示
• 回归系数的显著性水平。
• 通过 回归系数表，我们可以清晰地看到 模型的自变量及对应的回归系数、显著性检验结果、重要性，
• 每个自变量的显著性水平都小于0.01，说明每个自变量的回归系数具有极其显著的统计学意义。
• 
  
• 2.9 均值线图
• 
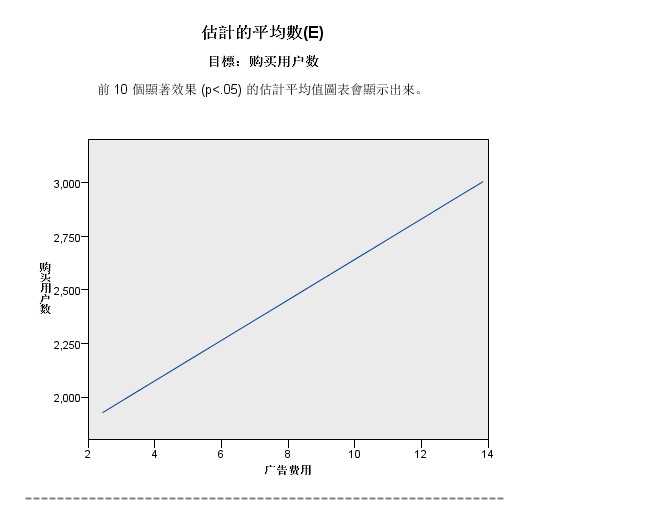                            图 2-9 均值线图
  
• 第九张图是因变量与各个自变量绘制的均值，用直观地图形方式帮助我们研究因变量与各个自变量之间的关系。
• 不显著的自变量不会生成对应的均值线图。如图，“广告费用 ”与“购买用户数”之间存在着明显的线性关系。
• 
  
• 2.10 模型构建摘要
• 
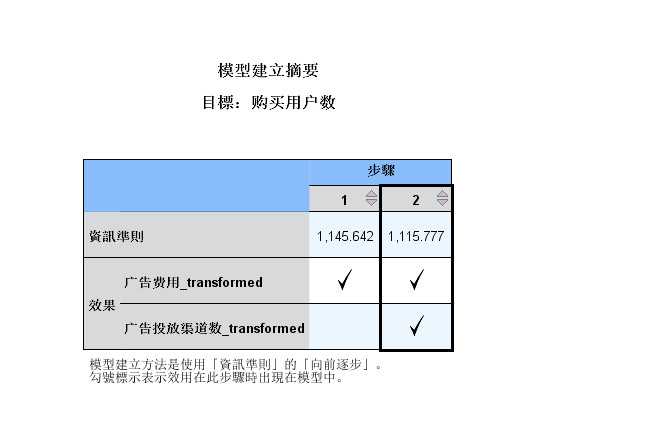                           图2-10 模型构建摘要表
  
• 第十张图为模型构建摘要表，用于输出模型构建过程信息，可以看到模型的信息准则值(AICc)是从左到右依次递减，
• 数值越小，表示模型效果好，也就是说，随着自变量逐渐被选择进入模型，使得模型拟合效果越来越好。
• 
  
• 3. 模型预测
• 
  
  
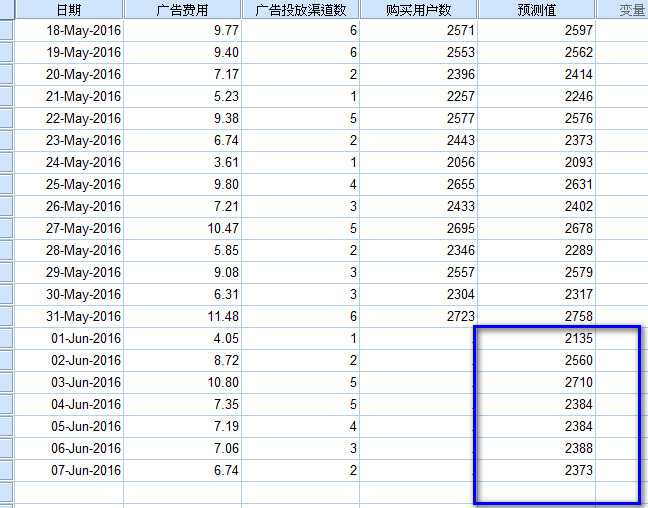                          图3-1 数据预测值输出结果
  
• 在参数设置中，我们勾选了【将预测值保存到数据集】，SPSS已经在数据集中最后一列增加了一个新变量：预测值。
• 如图3-1，数据集中最后一列就是预测值，这样就可以根据6月1日至7日广告投放计划，预测得到6月1日至7日
• 的购买用户数。

来自为知笔记(Wiz)