深度学习“深度学习”-概念篇
Posted zrq96
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习“深度学习”-概念篇相关的知识,希望对你有一定的参考价值。
Q:什么是“深度学习”
对于“深度学习”这个术语,一个粗浅的定义是“主要使用深度神经网络为工具的机器学习算法”。深度学习首先是一类机器学习的方法,因为它和其他机器学习方法一样允许计算机从样本中、从实例中、从数据中使用统计手段“学习”出规律来,而不用像专家系统和其他符号主义的方法一样人工定义规则。其次,深度学习不同于其他机器学习方法的地方,在于它主要的工具,或者说使用到的数学模型是深度神经网络。
虽说深度学习这个词时近几年才后起来,但是它在1986年甚至更早就被提出来了。早在19世纪60年代最简单的人工神经网络——多层感知机就已经现世。19世纪八九十年代,联结主义学术思潮对人工神经网络的研究进一步加深。在这一时期,许多现在大热的模型,如卷积神经网络和循环神经网络就被提出了;而许多现在的学术大牛,如Hinton,LeCun,Bengio也在那个时期初露锋芒。由于当时的数据量和算力不足的原因,神经网络不如SVM等简单的算法好用,但2006年左右,Hinton 和 Salakhutdinov 发现多层前馈神经网络可以先通过逐层预训练,再用反向传播(Back Propagation)算法进行精调的方式进行有效学习,算法深度学习得以获得不输于SVM等算法的实用性。随着移动互联网的提出和摩尔定律进一步发挥作用,数据量和算力也上来了,深度学习方法也越来越好用。在2012年的ImageNet图像识别比赛上,深度学习方法方法以优于第二名10个百分点的绝度优势获胜,至此一战成名。2016年,AlphaGo击败李世石,从此深度学习天下皆知。更多深度学习的历史可以参考由Ian Goodfellow、Yoshua Bengio、Aaron Courville合著的《Deep Learning》 第一章,中文世界比较好的资料是复旦大学邱锡鹏 写的《神经网络与深度学习》第一章。
Q:人工神经网络的本质是什么?
一个函数
人工智能的各种算法都是数学模型,人工神经网络不例外。从数学角度看,一个人工神经网络,本质上就是一个函数,一个从输入到输出的映射。更具体一点,神经网络是有多个简单函数组合而成的符合函数。
我们知道,人工神经网络的基本单元是人工神经元,任何神经网络都是神经元堆叠组合而成。神经元也是一个简单的函数。周志华的《机器学习》第五章中有一个图[3]很简洁美观地描绘了一个神经元的经典结构。

简单来说,一个神经网络就是一个线性组合与一个非线性函数的复合函数,就是把线性组合的结果丢进一个非线性函数里[4]。
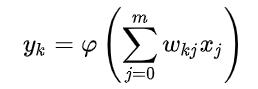
一个概率分布函数
一个人工神经网络是一个概率分布函数。这其实不足为奇,应该说任何机器学习模型,或者说统计学习模型都是概率分布函数。毕竟机器学习的根本目标是预测:预测(判断)某张图片的类别、预测某间房子的房价、预测某日的天气情况、预测某个时段的车流量、预测某个用户喜欢的商品、预测某条广告的点击率······既然是预测,则必然用到概率模型。哪怕是最基本的线性回归模型:y = w1 * x1 + w2 * x2 + b 背后也是正态分布概率模型(将y看做x的随机变量,求y的条件概率分布,具体看Stanford的cs229-note-1, 中文看这篇文章)
同样,每个神经网络的输出都是输入的随机变量,每个神经网络都是一个参数化条件概率模型,也正是因为如此,基本上所有神经网络都可以用最大似然评估(MLE)来优化。
多个Logistic回归模型的组合
有一点机器学习知识的人都知道,如果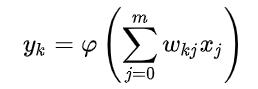 图中的外层函数为sigmoid函数,哪怕外层函数为relu或者tanh,我们也可以将它看做广义的logistic模型。如此一来,一个神经元其实就是一个logistic回归模型。那么多个神经元连接起来的神经网络,本质上就是多个logistic回归模型的分层组合。
图中的外层函数为sigmoid函数,哪怕外层函数为relu或者tanh,我们也可以将它看做广义的logistic模型。如此一来,一个神经元其实就是一个logistic回归模型。那么多个神经元连接起来的神经网络,本质上就是多个logistic回归模型的分层组合。
Q:神经网络背后的设计思想是什么?
或问:为什么将多个神经元(Logistic回归模型)连在一起就能有这么强大的威力?
关于这个问题有那么一种解释:神经网络是分层的,浅层的神经元可以提纯出更有价值的信息给深层的神经元处理。至于哪些信息是“更有价值的信息”,可以通过不断试错(最小化损失函数)来确定。一个Logistic模型不给力,我们可以用多几个。当然不是全部一起上,而是让这些个Logistic模型分工合作。维基百科上的说法是:
neural networks employ a hierarchy of layered filters in which each layer considers information from a prior layer (or the operating environment), and then passes its output (and possibly the original input), to other layers.
这一种解释特别适用于图像识别的卷积神经网络。比如说浅层的神经元可以学习到图片某个区域是否存在曲线/直线/弧线,深层的神经元可以学习到图片的某个区域是否存在一只眼睛/耳朵/鼻子,更深层的神经元可以学习到这张图片是否存在一只猫/狗。就像2009年ICML的一篇论文[2] :
The visual world can be described at many levels: pixel intensities, edges, object parts, objects, and beyond. The prospect of learning hierarchical models which simultaneously represent multiple levels has recently generated much interest. Ideally, such “deep” representations would learn hierarchies of feature detectors, and further be able to combine top-down and bottom-up processing of an image. For instance, lower layers could support object detection by spotting low-level features indicative of object parts. Conversely, information about objects in the higher layers could resolve lower-level ambiguities in the image or infer the locations of hidden object parts.

本图取自上文提到的论文,将一个卷积网络的第一、二层的数值输出以图片数据格式查看后可以看到,这个卷积网络的第一、二层其实就是一个能够识别类似“黑线、白线、黑线”这样的组合的分类器。
我们也可以认为,浅层的神经元是深层神经元的预处理器,浅层的logistic回归模型做了一些如“这里有直线,那里有弧线”,或者“这一点属于A类,那一点属于B类”这样的简单分类工作,深层的logistic回归模型做一些“这只是猫,那只是狗”这样的高层次的分类工作。
Q:深度学习作为一门学问,其知识结构是怎样的?
《Deep Learning》[5]作为目前比较权威的深度学习教科书,其编排是是很能反映目前这一学科的知识体系的。书的第一章介绍了该书的知识结构,这里截取了第二第三部分(第一部分是基本的数学和机器学习知识)。
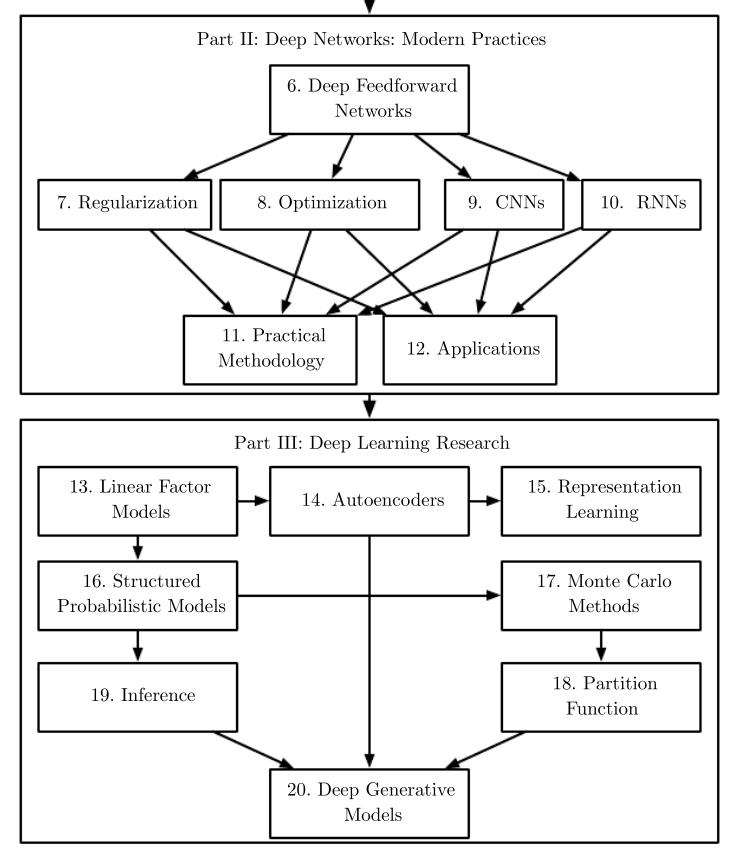
由图可知,作者把目前深度学习的知识体系分为两部分,一部分是比较成熟的基础部分,另一部分是仍在发展的前沿部分。作为深度学习这一学科的基础,深度前馈神经网络(多层感知机)体现了深度学习最最基础的思想,定义了深度神经网络的基本单元、一般结构,并凝结了一套设计网络和优化网络的通用方法。其他所有变种都衍生自深度前馈神经网络。掌握了前馈网络,就可以进一步学习正则化和更多优化技巧,前者是一类提高模型泛化能力的方法,后者是提高神经网络性能和加快训练效率的方法。除了设计和调优的技巧以外,还要进一步学习前馈神经网络的一些改良版本,相较于普通的前馈网络,这些改良版本针对特定问题做了特定的网络结构改进,在各自的领域有高于普通前馈网络的效果。最典型的是卷积神经网络和循环神经网络。前者在图像识别领域有奇效,后者主要用于序列建模,比如自然语言处理。学完这四个模块的比较理论化的内容,就可以通过一些前辈的经验掌握一些最佳实践和应用。
以上就是深度学习的基础内容。至于更高级的内容,比如自编码器、表示学习,与蒙特卡洛方法的结合(ALphaGo),推理,以及没有在《Deep Learning》出现的强化学习,这些研究方向还在蓬勃发展。想要学习这些前沿技术,除了掌握扎实的基础知识和阅读《Deep Learning》这类综述文献意外,也只能从会议和期刊的论文中学习了。
Q:“深度学习可解释性差”是什么意思?
解释,就是在观察的基础上进行思考,合理地说明事物变化的原因,事物之间的联系,或者是事物发展的规律。(搜狗百科)
“深度学习可解释性差”,意思就是我们很难说明一条样本数据灌进一个神经网络出来这样一个预测结果的原因,这造成的直接后果就是很多时候我们不知道怎么针对一个神经网络做优化。
考虑一个线性回归模型,比如我用房屋面积x1和到市中心的距离x2两个因素来预测房价y:y = w1 * x1 + w2 * x2 + b我们知道如果w1 = 10, w2=1000就意味着x1增加1,y增加10,x2增加1,y增加1000,亦即我们认为一个房子的房价受房屋大小和到始终细腻距离两个因素影响,而且到市中心距离这个因素的印象力很大,比房屋面积大100倍。我们还可以针对每个权重w和偏置b做假设检验,来看看这三个因素有没有哪些是无显著影响的。对于这种只有两个因素的线性模型,我们甚至还可以将模型的函数图像画出来,直观地检查模型与数据拟合程度如何。对于线性模型,我们很清楚每一个参数w和b的含义是什么——我们很清楚这个模型学习了什么东西。所以我们可以有很明确的优化方案:“深圳市大城市,里市中心越近房价越高,我们应该提高到市中心距离这个因素的权重,加大w2”。
然而神经网络,一来神经元多,参数众多;而来结构分层,且隐含层众多;三来神经网络的参数对应的特征不是人工设计的,是神经网络在学习过程中自己选择的。我们根本不知道我们的神经网络模型到底学习了写什么,我们不知道每一个参数的含义是什么,所以我们无法解释整个模型的运作机制,自然也无法得出明确而又针对性的优化方案。
可解释性差也是深度学习目前最大的缺陷之一。这篇文章很详细地阐释了可解释性的概念,推荐阅读。
本作品首发于简书 和 博客园平台,采用知识共享署名 4.0 国际许可协议进行许可。
本文直接或简介地使用了以下著作的内容:
- Honglak Lee, Roger Grosse, Rajesh Ranganath and Andrew Ng "Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations"
- 周志华的《机器学习》
- Wikipedia "Artificial Neuron"
Ian Goodfellow, Yoshua Bengio, Aaron Courville 《Deep Learning》
以上是关于深度学习“深度学习”-概念篇的主要内容,如果未能解决你的问题,请参考以下文章
(机器学习深度学习常用库框架|Pytorch篇)第一节:Pytorch简介和其核心概念
对比学习资料《深度学习入门:基于Python的理论与实现》+《深度学习原理与实践》+《深度学习理论与实战基础篇》电子资料