深度学习--基于深度矩阵分解的属性表征学习
Posted vast_w
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习--基于深度矩阵分解的属性表征学习相关的知识,希望对你有一定的参考价值。
基于深度矩阵分解的属性表征学习
原文地址:http://blog.csdn.NET/hjimce/article/details/50876956
作者:hjimce
一、相关概念
本篇博文主要讲解文献《A deep matrix factorization method for learning attribute representations》。这篇主要借助于深度学习的思想,提出贪婪的半非负矩阵分解SNMF方法,其思想与栈式自编码网络一样的训练方法,首先通过逐层分解作为预分解结果,然后再整体微调训练。因为这篇文献我看到后面,感觉计算量非常大,不是很喜欢这文献,所以我也没有全部细看。
虽然文献一开始讲的是深度半非负矩阵分解,属于线性分解。不过作者对目标优化函数进行了多次进化,同时还结合了半监督约束项,因此到了最后算法基本上就跟神经网络非常类似了(也包含了非线性激活函数映射)。
开始讲解paper前,先学一些基础概念:
(1)矩阵分解简单概述
在机器学习领域,矩阵分解家族是经常遇到的一类算法,如:PCA、K-means、NMF、SNMF、谱聚类、稀疏编码、SVD、白化、ICA等,它们的目标基本上都是对X矩阵进行分解:
X=Z*H
然后不同的算法,采用不同的约束条件(对Z、H进行约束),具体请参考文献《The Advanced Matrix Factorization》。在机器学习中,特征这个词具体是什么东西?如果从矩阵分解的角度来讲的话:
X=Z*H
X是训练样本。矩阵Z根据不同的应用场景,又可以称之为:权值矩阵、基矩阵(如PCA)、字典(如稀疏编码、k-means)、变换矩阵。
矩阵H也称之为:特征矩阵、投影坐标、系数矩阵、编码矩阵(如稀疏编码、k-means)。矩阵分解家族基本上都是无监督学习算法,而所谓的无监督表征学习,说的简单一点就是求解H矩阵。
(2)非负矩阵分解NMF定义
非负矩阵分解定义:给定样本矩阵X=[x1,x2……xn],其中该矩阵的每一列表示一个样本,矩阵的所有元素都是非负的(比如x的每一列是一张图片样本,x中的元素都是非负的),非负矩阵分解的目标就是要对X进行分解,公式如下:

并且分解后的矩阵Z、H都是非负矩阵(矩阵元素都是非负的),其中Z称之为基矩阵,H称之为系数矩阵。
(2)半非负矩阵分解SNMF定义
为了扩展非负矩阵的应用场景,有时候我们的样本矩阵X并不是非负矩阵,于是就有了半非负矩阵:

半非负矩阵只是要求H为非负矩阵,对于数据矩阵X和基矩阵Z并没有要求。这个思想和聚类量化一样,Z的每一列表示聚类中心并不需要做非负约束,H表示特征矩阵,这使得我们可以从原始数据中学习到低维的特征。
二、基础回顾
这一部分先简单复习一下单层的半非负矩阵分解算法。
1、与k-means的关系
半监督非负矩阵分解和k均值聚类很相似。半非负矩阵分解中,我们允许数据矩阵X和因子矩阵Z中的元素可正可负,同时约束H矩阵为非负矩阵:
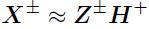
从聚类的角度来讲,Z=[z1,z2……zn]的每一列就是我们的聚类中心,H的每一列就是我们的编码矢量。如果对半非负矩阵分解,加入约束条件H是行正交矩阵,即H*H^T=I,同时H的每一列只有一个正数,其它的都为0:
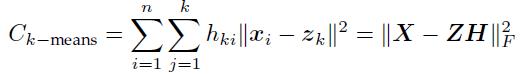
半非负矩阵与k均值聚类的区别在于:半非负矩阵分解并没有要求H矩阵的行向量是相互正交的,我们也可以把它看成是软聚类,k-means可以看成是SNMF的特例。
2、半非负矩阵求解算法
目标函数:
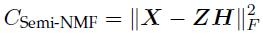
我们的目标是求解Z、H,可以采用固定其中的一个,然后更新另外一个变量:
(1)首先固定H矩阵,那么我们就可以求解Z:
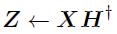
其中H+表示H矩阵的伪逆矩阵。
(2)更新H矩阵:
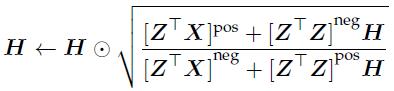
因为我们要求H矩阵是非负矩阵,因此我们就需要采用上面的矩阵进行更新,其中Apos矩阵表示:
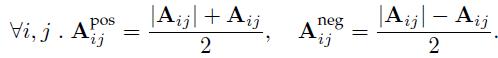
Apos表示把矩阵所有负值元素全部置0,剩下的非负矩阵。反之,Aneg就表示负矩阵,也就是矩阵中正的元素全部置0
具体matlab源码实现如下:
[python] view plain copy

- Z = X * pinv(H);%更新Z矩阵
- A = Z' * X;%求Z的转置乘以X
- Ap = (abs(A)+A)./2;
- An = (abs(A)-A)./2;
- B = Z' * Z;%Z^T*Z
- Bp = (abs(B)+B)./2;
- Bn = (abs(B)-B)./2;
- H = H .* sqrt((Ap + Bn * H) ./ max(An + Bp * H, eps));%更新H矩阵总公式
三、算法概述
虽然一开始文献讲解的是深度半非负矩阵的分解,不过到了最后算法经过了好几个阶段的进化,结合了非线性激活函数、半监督学习约束,所有到了最后公式基本已经跟最初的半非负矩阵分解区别很大了。文献算法的讲解从多层线性分解-》非线性分解-》半监督非线性分解,进行算法的进化,下面先简单讲解文献的总体思路。
1、第一次进化:深度线性分解
文献首先先提出了深度半非负矩阵分解公式:

这部分需要我们学习的主要是:逐层贪婪分解、整体损失微调。
2、第二次进化:深度非线性分解
因为线性分解不能表达复杂的特征,所以在步骤1的基础上,引入了非线性激活函数:
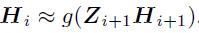
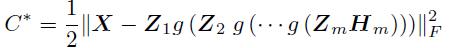
g表示非线性激活函数,这样就跟神经网络非常相似了。
3、第三次进化:弱监督非线性分解
在步骤2的基础上,加入了约束项,结合先验知识在里面,使得每一层分解的特征矩阵H符合我们所需要的属性(如果没有监督,那么是自动分解X):
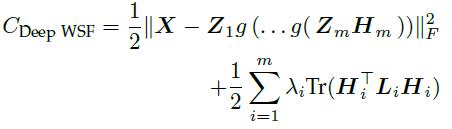
也就是引入了约束项Tr(H^T*L*H)。
四、第一次进化——深度线性分解
1、相关描述
OK,终于到了关键部分了。对于SNMF我们的目标是求解一个低维H+矩阵,用于表征原始的数据X。在大部分情况下,我们所要分析的数据X属性是未知的,其包含着多种属性,比如paper所要处理的人脸图片是各种角度、光照、表情、以及不同的人。因此我们采用多层分解,相比于单层的SNMF来说,更能表达出人脸的多种属性。下面是单层分解与多层分解示意图:
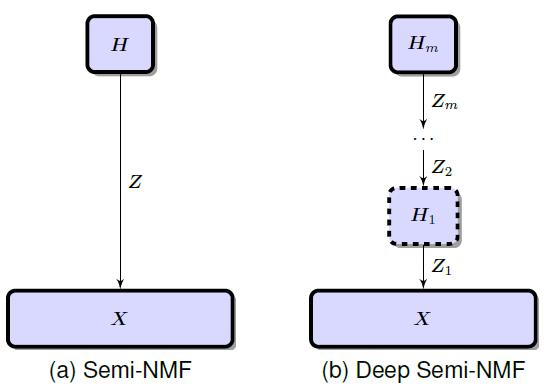
文献提出了深度半非负矩阵分解模型,给定数据X我们把它分解层M+1个因子:
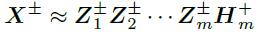
这个也可以写成:
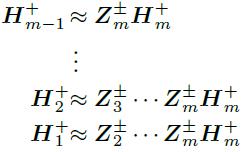
通过每一层的分解,每一层提取到的特征Hi,然后我们可以对每一层H实现相应的任务。比如文献示意图如下,其对每一层的H做了k-means聚类,可以聚类出不同的属性。
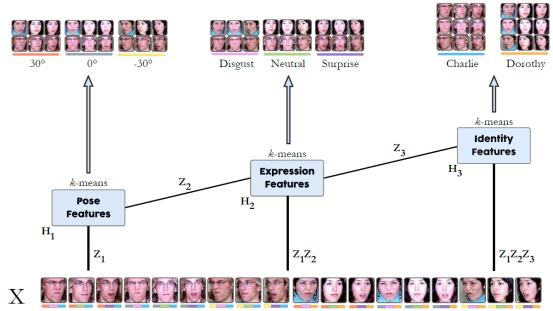
这个具体可以看一下最上面聚类结果。
2、算法实现
采用类似于栈式自编码网络一样的训练方法,分成逐层预训练、整体微调两个阶段。
(1)预训练阶段。
A、把X=Z1*H1,完成第一层分解;
B、对H1继续分解H1=Z2*H2,完成第二层分解;
如此循环下去,把所有的层都进行了预训练。
(2)整体微调。通过最小化损失函数:

这一步通过求解偏导数,然后继续进行梯度下降,具体公式推导看文献。最后的伪代码实现为:

主要分为逐层预分解和整体微调两个阶段。
后面文献还了引入非线性、半监督,因为我感觉计算量越来越大,学到的东西不是很多,所以就没有具体细看后面各种公式的推导。最后文献算法的伪代码为:

个人总结:这篇文献主要是把深度学习的方法,引入矩阵分解中,实现深度无监督表征学习,思想值得我们学习;然而这篇文献的整个过程,感觉完全不考虑计算量,对于学术研究是不错的文献,但是对于工程应用那就……
参考文献:
1、《A deep matrix factorization method for learning attribute representations》
以上是关于深度学习--基于深度矩阵分解的属性表征学习的主要内容,如果未能解决你的问题,请参考以下文章