KMP算法分析

Posted 2021-02-01 dongry

根据博主July的https://blog.csdn.net/v_july_v/article/details/7041827所载，记录个人理解心得(红色部分为个人理解)：

1.KMP算法流程

  假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置
  1.如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；(当S{i]==P[j]时，说明模式串j前面的字符都与文本串i前面对应的字符匹配成功)

    

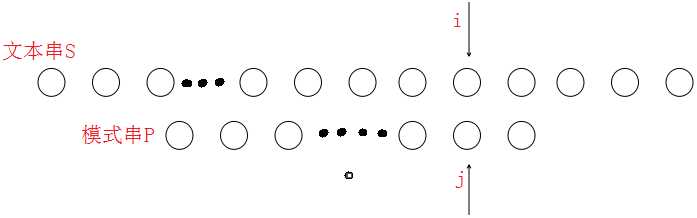
  2.如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。(next[j]为j前面字符所拥有的相同的最大前缀和后缀)
    即当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next值,即移动的实际位数为：j - next[j]，且此值大于等于1

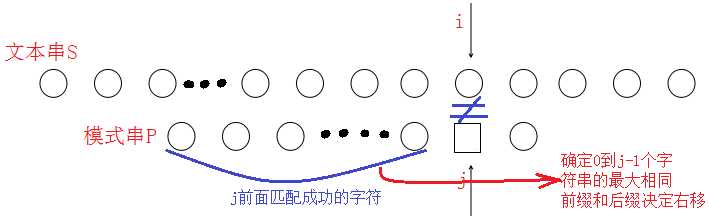
  如果next [j] 等于0或-1，则跳到模式串的开头字符，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头，且具体跳过了k 个字符。

int KmpSearch(char* s, char* p)
{
    int i = 0;
    int j = 0;
    int sLen = strlen(s);
    int pLen = strlen(p);
    while (i < sLen && j < pLen)
    {
        //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++    
        if (j == -1 || s[i] == p[j])
        {
            i++;
            j++;
        }
        else
        {
            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]    
            //next[j]即为j所对应的next值      
            j = next[j];
        }
    }
    if (j == pLen)   //返回模式串在文本串的起始位置(当j==pLen时，说明已经匹配完成，所以其在文本串的起始点为i-j)
        return i - j;
    else
        return -1;
}

2. 前缀后缀最长公共元素长度

  公式：p₀ p₁ ...p_k-1 p_k = p_{j- k} p_j-k+1...p_j-1 p_j(左右两边原因下标相加为j)

  所以最大长度为k+1（因为是从0开始计数，到k结束）

  如：

  

  数组的next[i](0~i)值，表示的是当前字符之前的最大相同前后缀的值，如next[9]指的是ABCDEFGAB的最大相同前后缀；相当于最大相同前后缀平移1位，然后补-1；

3. next数组匹配

  匹配失配，j=next[j]，模式串向右移动的位数为：j-next[j]。换言之，当模式串的后缀pj-k pj-k+1, ..., pj-1 跟文本串si-k si-k+1, ..., si-1匹配成功，但pj 跟si匹配失败时，因为next[j] = k，相当于在不包含pj的模式串中有最大长度为k 的相同前缀后缀，即p0 p1 ...pk-1 = pj-k pj-k+1...pj-1，故令j=next[j]，从而让模式串右移j- next[j] 位，使得模式串的前缀p0 p1, ..., pk-1对应着文本串 si-k si-k+1, ..., si-1，而后让pk 跟si 继续匹配。如下图所示：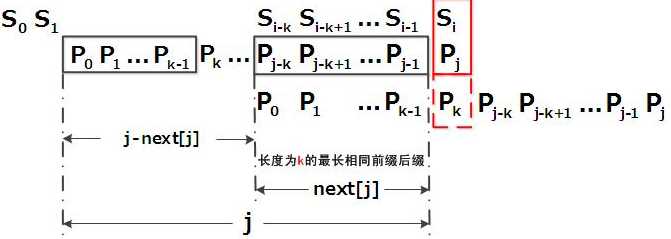

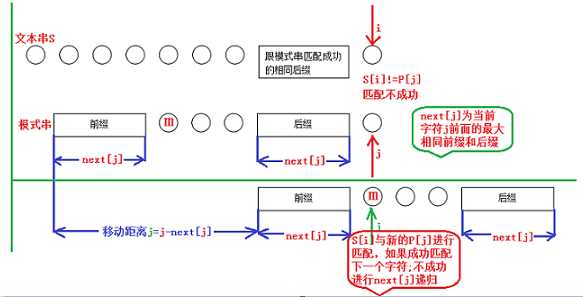
4 程序

#include <stdio.h>
#include <string.h>
void Next(char*S,int *next)
{
    int i=1;
    next[1]=0;
    int j=0;
    while (i<strlen(S)) 
    {
        if (j==0||S[i-1]==S[j-1]) 
        {
            i++;
            j++;
            next[i]=j;
        }else
        {
            j=next[j];
        }
    }
}

int KMP(char * S,char * s){
    int next[10];
    Next(s,next);//根据模式串T,初始化next数组
    int i=1;
    int j=1;
    while (i<=strlen(S)&&j<=strlen(s)) 
    {
        //j==0:代表模式串的第一个字符就和当前测试的字符不相等；S[i-1]==s[j-1],如果对应位置字符相等，两种情况下，指向当前测试的两个指针下标i和j都向后移
        if (j==0 || S[i-1]==s[j-1]) 
        {
            i++;
            j++;
        }
        else
        {
            j=next[j];//如果测试的两个字符不相等，i不动，j变为当前测试字符串的next值
        }
    }
    if (j>strlen(s)) 
    {                   //如果条件为真，说明匹配成功
        return i-(int)strlen(s);
    }
    return -1;
}
int main() 
{
    int i=KMP("ababcabcacbab","abcac");
    printf("%d",i);
    return 0;
}

---------------------
感谢博主v_JULY_v
原文：https://blog.csdn.net/v_july_v/article/details/7041827