协方差 的直观理解

Posted 2021-02-01 zhuimengzhe

1.协方差

方差是描述自身偏离其均值的程度。

协方差用来描述两个变量间的变化关系,协方差用来度量两个随机变量关系的统计量

[ cov(X,Y)=E[(X-E[X])(Y-E[Y])] ]

[ cov(X,Y)=E[(X-μ_x)(Y-μ_y)] ]

E[x] 代表期望，一般置X的均值

公式：如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值

eg：比如有两个变量X,Y，观察t1-t7（7个时刻）他们的变化情况。

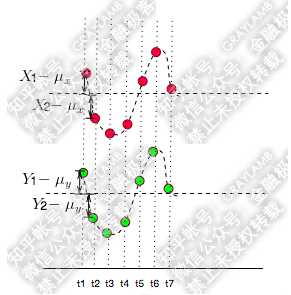
我们发现在每一个时刻，X-μ，和Y-μ 都是同号的，

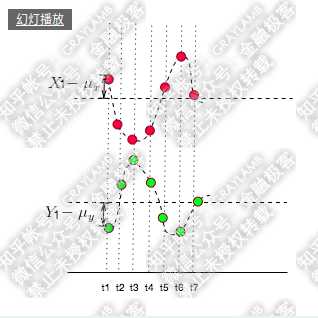
如果是反向的：X-μ，和Y-μ 的乘积就是负号，

当然上面说的是两种特殊情况，很多时候X，Y的运动是不规律的，比如：

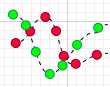
这种情况下很可能在某一个时刻 乘积是正，另外一个时刻乘积又为负数了，将每一个时刻的乘积加到一起，其中的正负会抵消，最后平均得出值就是协方差，通过协方差的大小，就可以判断两个变量同向或者反向的程度了。

总结一下，如果协方差为正，说明X，Y同向变化，协方差越大说明同向程度越高；如果协方差为负，说明X，Y反向运动，协方差越小说明反向程度越高。

拓展

如果同向变化，但是X大于均值，Y小于均值，那乘积是负数的。

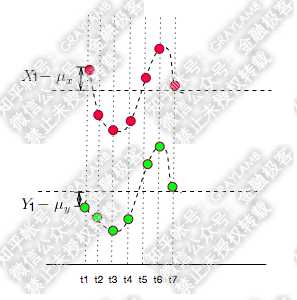
可见t1时刻 X-μ，和Y-μ 负号相反，乘积为负。但是如果从整体来说依然要计算其他时间的值，然后在吧7个时间的值求均值，所以某一时刻的为负数不代表整体是反向的。要结合整体来判断。

相关系数

翻译一下：就是用X、Y的协方差除以X的标准差和Y的标准差。

所以，相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

既然是一种特殊的协方差，那它：

1、也可以反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。

2、由于它是标准化后的协方差，因此更重要的特性来了：它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。
[ ρ=frac{Cov(X,Y)}{δ_Xδ_Y} ]
首先，还是承接上文中的变量X、Y变化的示意图（X为红点，Y为绿点），来看两种情况：

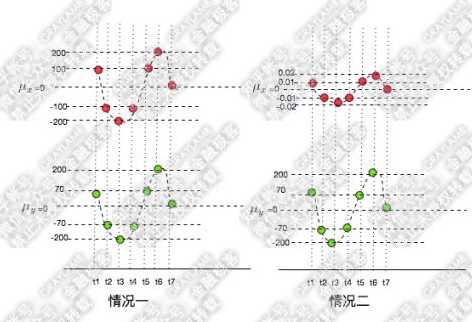
很容易就可以看出以上两种情况X，Y都是同向变化的，而这个“同向变化”，有个非常显著特征：X、Y同向变化的过程，具有极高的相似度！无论第一还是第二种情况下，都是：t1时刻X、Y都大于均值，t2时刻X、Y都变小且小于均值，t3时刻X、Y继续变小且小于均值，t4时刻X、Y变大但仍小于均值，t5时刻X、Y变大且大于均值……

可是，计算一下他们的协方差，

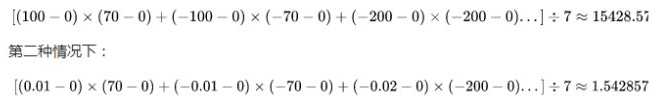
协方差差出了一万倍，只能从两个协方差都是正数判断出两种情况下X、Y都是同向变化，但是，一点也看不出两种情况下X、Y的变化都具有相似性这一特点。

这是为什么呢？

因为以上两种情况下，在X、Y两个变量同向变化时，X变化的幅度不同，这样，两种情况的协方差更多的被变量的变化幅度所影响了

所以，为了能准确的研究两个变量在变化过程中的相似程度，我们就要把变化幅度对协方差的影响，从协方差中剔除掉。于是，相关系数就横空出世了，就有了最开始相关系数的公式：

那么为什么要通过除以标准差的方式来剔除变化幅度的影响呢？咱们简单从标准差公式看一下：
[ δ_X=sqrt{E((X-μ_x)^2)} ]
从公式可以看出，标准差计算方法为，每一时刻变量值与变量均值之差再平方，求得一个数值，再将每一时刻这个数值相加后求平均，再开方。

为何要做平方呢，因为有时候变化值和均值是反向偏离的X-μ是一个负数，平方后就可以吧负号消除，最后求出每次变化偏离均值的情况。刚才为了消除负号问题加了平方，最后需要开方，将数值再返回到原有的量级，

所以标准差描述了变量在整体变化过程中偏离均值的幅度。协方差除以标准差，也就是把协方差中变量变化幅度对协方差的影响剔除掉，这样协方差也就标准化了，它反应的就是两个变量每单位变化时的情况。这也就是相关系数的公式含义了。

相关系数是协方差除以标准差，当X,Y的波动幅度变大的时候，协方差变大，标准差也会变大，相关系数的分母都变大，其实变化的趋势是可以抵消的，协方差的取值范围是 正无穷到负无穷，相关系数则是+1 到-1之间。

当他们的相关系数为1时，说明两个变量变化时的正向相似度最大，即，你变大一倍，我也变大一倍；你变小一倍，我也变小一倍。也即是完全正相关（以X、Y为横纵坐标轴，可以画出一条斜率为正数的直线，所以X、Y是线性关系的）

随着他们相关系数减小，两个变量变化时的相似度也变小，当相关系数为0时，两个变量的变化过程没有任何相似度，也即两个变量无关。

当相关系数继续变小，小于0时，两个变量开始出现反向的相似度，随着相关系数继续变小，反向相似度会逐渐变大。

当相关系数为－1时，说明两个变量变化的反向相似度最大，即，你变大一倍，我变小一倍；你变小一倍，我变大一倍。也即是完全负相关（以X、Y为横纵坐标轴，可以画出一条斜率为负数的直线，所以X、Y也是线性关系的）。