王道数据结构内部排序算法总结

Posted 2021-01-31 hequnwang

首先看一下内部排序分类以及各个算法的时间复杂度、空间复杂度和稳定性

 

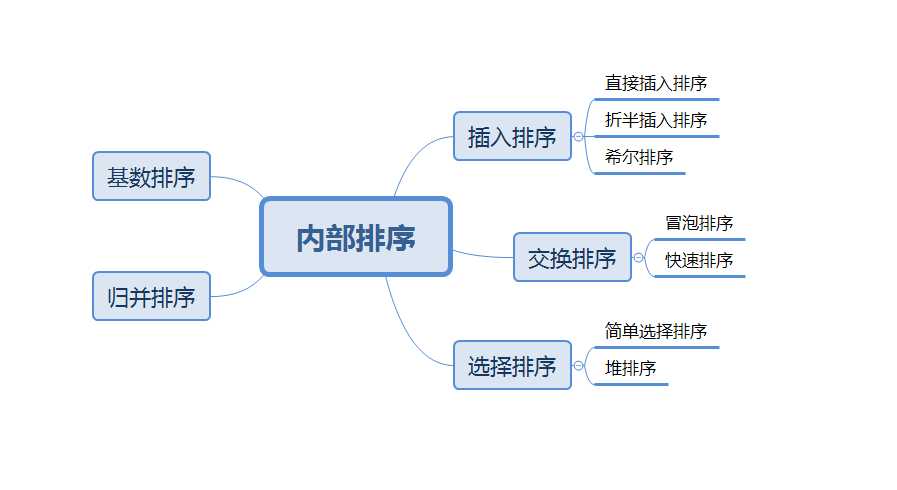
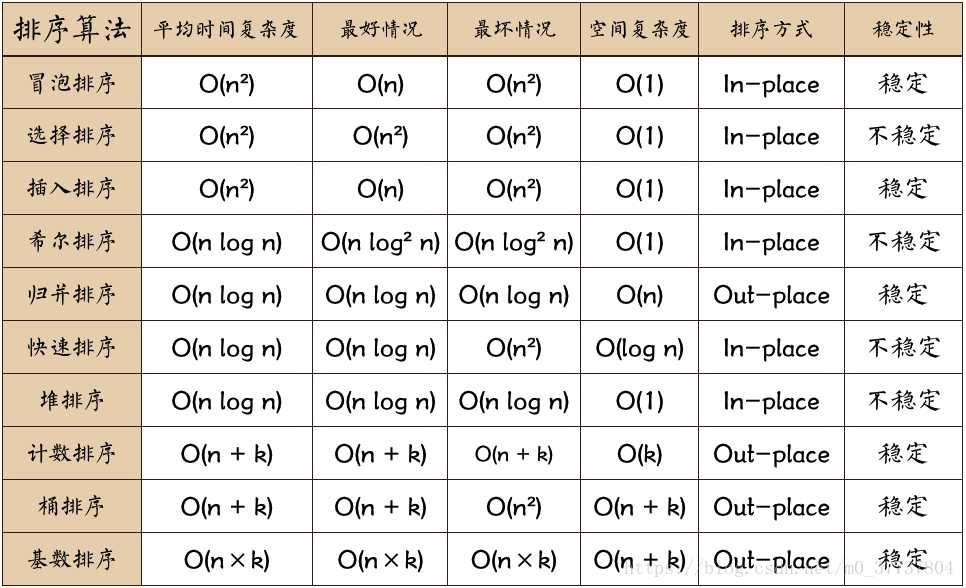
一、插入排序

　　1、直接插入排序 (Straight Insertion Sort)的基本思想是：把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

代码：

方法一：

void  InsertSort(ElemType A[],int n)
{
    int i,j;
    //使用哨兵
    for(int i = 2; i < n; i++)               //依次将A[2]~A[n]插入到前面已排序序列；

    {                                        
        if (A[i].key<A[i-1].key)             //若A[i]的关键码小于其前驱，需将A[i]插入有序表 
        {  
            A[0]<A[i];                       //复制为哨兵，A[0]不存放元素   
            for(j=i-1;A[0].key<A[j].key;--j) //从后往前找待插入位置
            {
                A[j+1]=A[j];                  //向后挪位；
            }
            A[j+1]=A[0];                       //复制到插入位置
        }
        
    }
    
}　　

方法2：

void insert_sort(int a[], int n)
{
    int i, j, k;

    for (i = 1; i < n; i++)
    {
        //为a[i]在前面的a[0...i-1]有序区间中找一个合适的位置
        for (j = i - 1; j >= 0; j--)
            if (a[j] < a[i])
                break;

        //如找到了一个合适的位置
        if (j != i - 1)
        {
            //将比a[i]大的数据向后移
            int temp = a[i];
            for (k = i - 1; k > j; k--)
                a[k + 1] = a[k];
            //将a[i]放到正确位置上
            a[k + 1] = temp;
        }
    }
}

 

      2、直接插入排序的时间复杂度和稳定性

　　  直接插入排序时间复杂度

　　　　直接插入排序的时间复杂度是O(N²)。
　　　　假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？N-1！因此，直接插入排序的时间复杂度是O(N²)。

　　  直接插入排序稳定性
　　　　直接插入排序是稳定的算法，它满足稳定算法的定义。
　　　　算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

 

3、代码实现

#include <stdio.h>
#include <stdlib.h>

//直接插入排序
void  InsertSort(int A[], int n)
{
    int i, j, k;

    for (i = 1; i < n; i++)
    {
        //为a[i]在前面的a[0...i-1]有序区间中找一个合适的位置
        for (j = i - 1; j >= 0; j--)
            if (A[j] < A[i])
                break;

        //如找到了一个合适的位置
        if (j != i - 1)
        {
            //将比a[i]大的数据向后移
            int temp = A[i];
            for (k = i - 1; k > j; k--)
                A[k + 1] = A[k];
            //将a[i]放到正确位置上
            A[k + 1] = temp;
        }
    }

}

//输出
void show_arr(int A[], int n)
{
    int i = 0;
    for (i = 0; i < n;i++)
    {
        printf("%d ", A[i]);
    }
}
int main()
{
    int sort_arr[9] = { 0,32, 34, 523, 53, 5, 65, 886, -35 };
    int i, j;
    InsertSort(sort_arr, 9);
    show_arr(sort_arr, 9);

    system("pause");
    return 0;
}

View Code