十大经典预测算法----线性回归

Posted 2021-01-31 baoxuhong

　　回归问题就是拟合输入变量x与数值型的目标变量y之间的关系，而线性回归就是假定了x和y之间的线性关系，公式如下：

        

　　如下图所示，我们可以通过绘制绘制（x,y）的散点图的方式来查看x和y之间是否有线性关系，线性回归模型的目标是寻找一条穿过这些散点的直线，让所有的点离直线的距离最短。这条完美直线所对应的参数就是我们要找的线性回归模型参数w1,w2,w3……b

　　

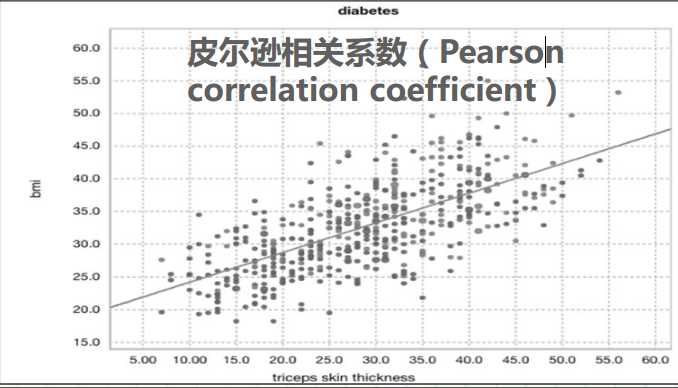
　　最小二乘法是一种求解回归模型参数w1,w2,w3……b的方法，线性回归模型中，能让预测值和真实值误差平方和最小的这条直线就是完美直线。

　　

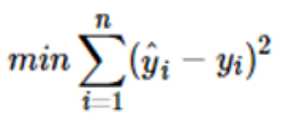
　　y^i表示第i个数据点的预测值，也就是对应完美直线的y值。最小二乘法通过求偏导数的方法让误差平方和取得最小值w1,w2,w3……b。

　　损失函数定义：

　　监督学习算法的目标就是为了让目标变量y的预测值和真实值尽量吻合，定义预测值与真实值之间的差异方法就叫损失函数。损失函数值越小，说明差异越小，模型的预测效果越好。线性回归中最小二乘法就是这个损失函数。

　　梯度下降法

　　在机器学习领域中，梯度下降法是更加通用的一种求解参数的方法。它的核心思想是 通过迭代逼近的方法寻找到让损失函数取得最小值的参数，如下图所示

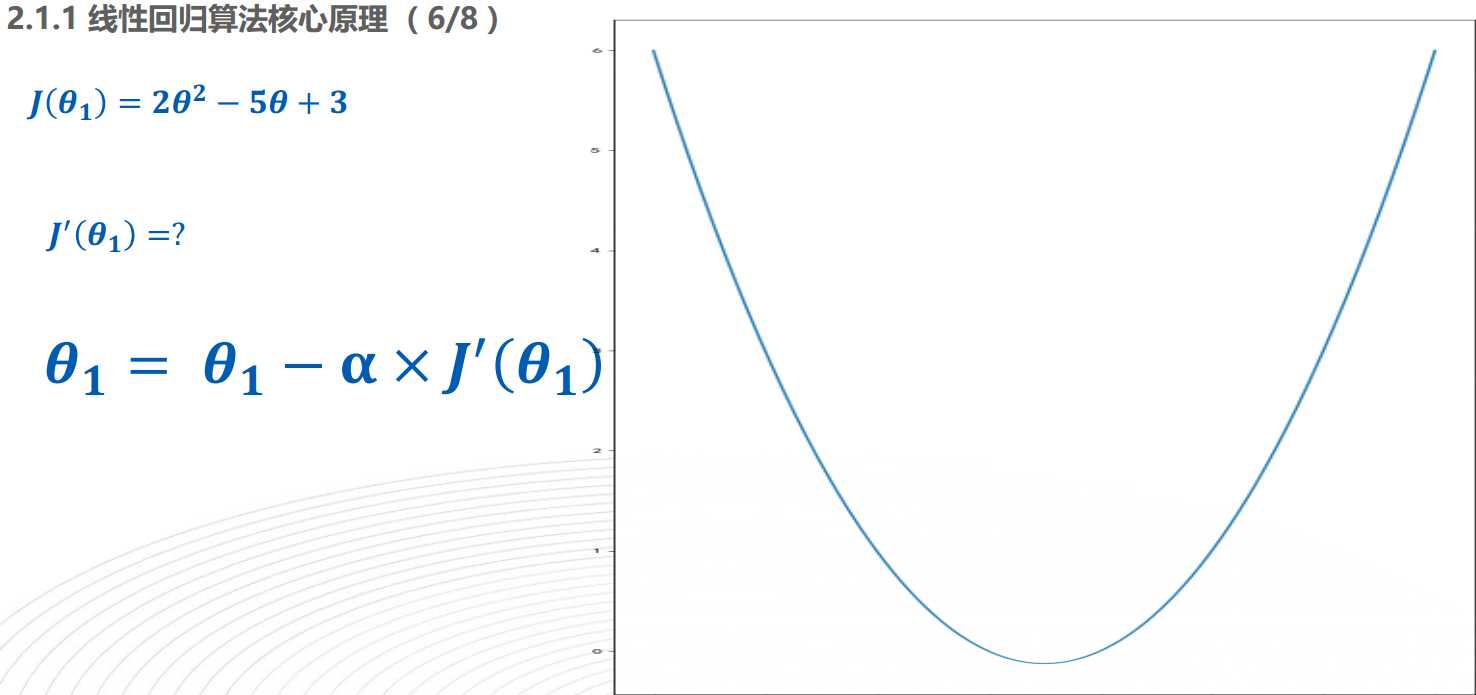
上图中，J(e)是损失函数，a是学习率，初始要设的小一点，这样用梯度下降法时，才会更快的迭代到。迭代过程如下所示：

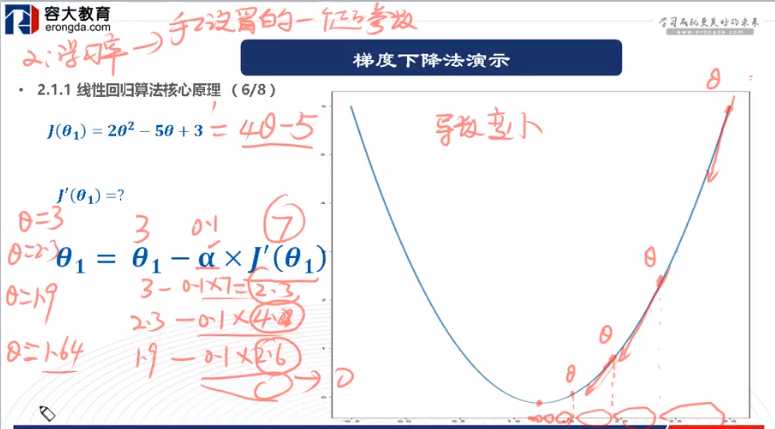
最终求出最合适的参数值