5.线性回归算法 4/20

Posted 2021-02-28 jwwzone

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

　· 我们先了解回归算法：

　　　　　　

　· 课上老师举了线性回归的应用：①房价预测；②销售额预测；③贷款额度预测；

 　　我们可以发现做线性回归，需要的数据都应该为连续型，最终要预测的因素成为目标值，把影响的因素成为特征；如果影响的因素只有一个，那么这就是一个单线性回归，如果有多个影响因素，那就是一个多线性回归。

　 ★ 我认为这里有一个重要的知识点就是：线性回归的数据应该是连续型的，如果拿到的数据如下图红色标点，那便不符合线性回归模型。

 

　　　　　　　

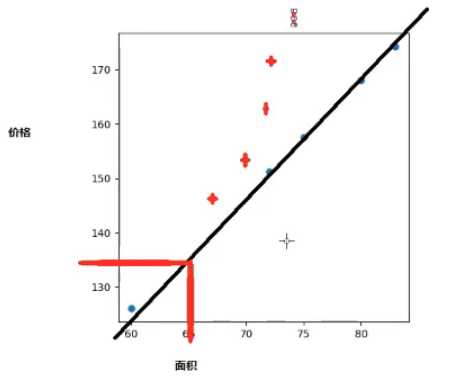
   · 线性回归模型：

　　　　　　

　　　（1）如果是一个变量，那就是二维空间；多个变量就是三维空间。

　　★（2）线性回归问题可以转换为矩阵乘积问题，矩阵在线性回归中扮演一个重要的角色。矩阵的计算正好满足线性回归的要求，所以矩阵的计算也是一个重点知识：

　　　　 ①数组与矩阵的特性与区别：

　　　　　

 　　　　②用代码比较数据和矩阵相乘的结果：

　　　　　　

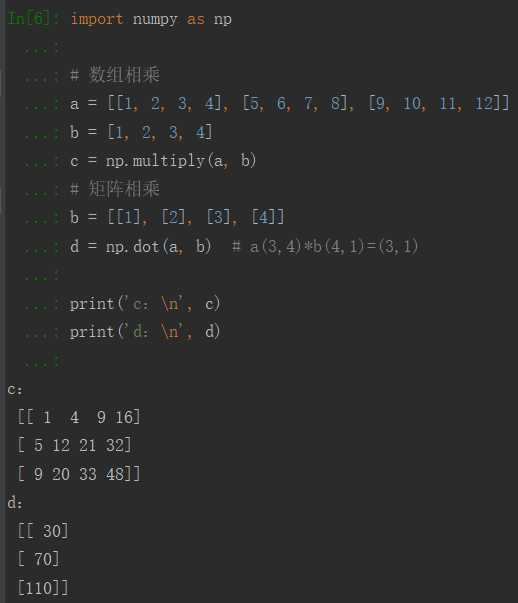
　 ·  机器学习需要迭代算法来减少误差，这里引入一个 损失函数（误差的大小）；学习的目的，就是将损失函数最小化：

　　　　　　

 

　　　　减少误差的方法（优化线性回归的策略）：

　　　　  ①正规方程：

　　　　　　　　　　

 

　　　  ★②梯度下降法：

　　　　　　　　　　

　　　　?为学习速率，学习速率的取值取决于数据样本。机器进行学习，多次迭代，如果损失函数在变小，说明结果越准确，取值准确。

　　　　关于梯度下降的具体概念可以参考：https://www.cnblogs.com/jwwzone/p/12684355.html的第二题。

　梯度下降代码：

# 梯度下降
import random
import time
import matplotlib.pyplot as plt

# 产生数据
_xs = [0.1 * x for x in range(0, 10)]
_ys = [12 * i + 4 for i in _xs]
print(_xs)
print(_ys)

w = random.random()
b = random.random()

a1 = []
b1 = []
for i in range(100):
    for x, y in zip(_xs, _ys):
        o = w * x + b  # 预测值
        e = (o - y)  # 误差
        loss = e ** 2  # 损失
        dw = 2 * e * x  # 对w求导
        db = 2 * e * 1  # 对d求导
        # 梯度下降，0.1为学习率
        w = w - 0.1 * dw
        b = b - 0.1 * db
        # 最终结果：loss越小越好，w接近12，b接近4
        print(‘loss={0},w={1},b={2}‘.format(loss, w, b))
    a1.append(i)
    b1.append(loss)
    plt.plot(a1, b1)
    plt.pause(0.1)

plt.show()

 

2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

　　可以用于：

　　（1）家庭家电的预测：①时间与功率之间的关系；②时间与电压之间的多项式关系。

　　（2）医学上可以预测年龄和血压的关系。

　　（3）预测一个发展的电信市场的网络容量。

 

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

 　　数据是我以前爬虫的广州市二手房数据，前几天爬了一次被抓到了哈哈。

　　 数据如下（获取单价和总价作为数据样本）：　　　　

　　　　　　 

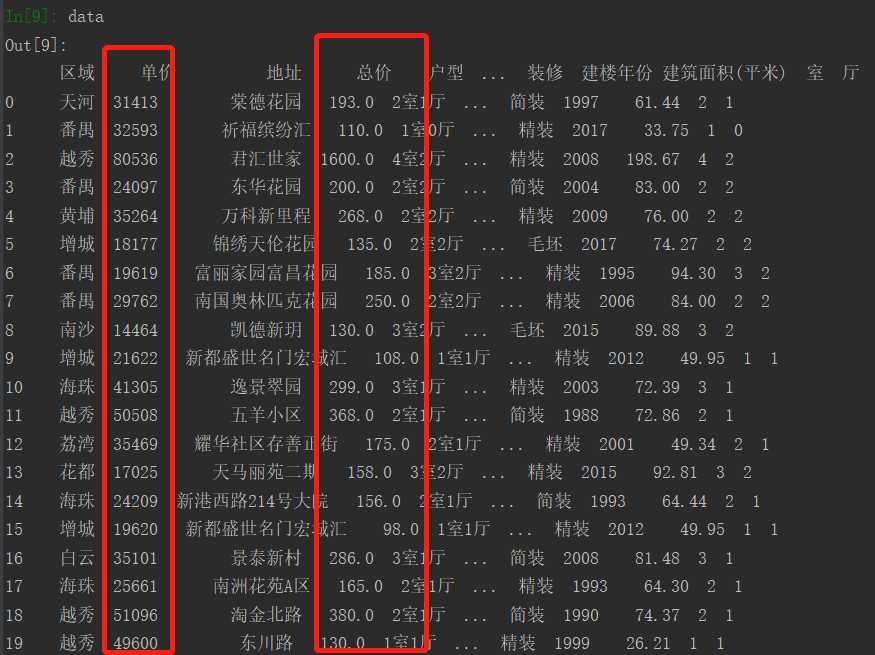
　　 用单价来预测总价，可视化结果如下：

　　　　　　

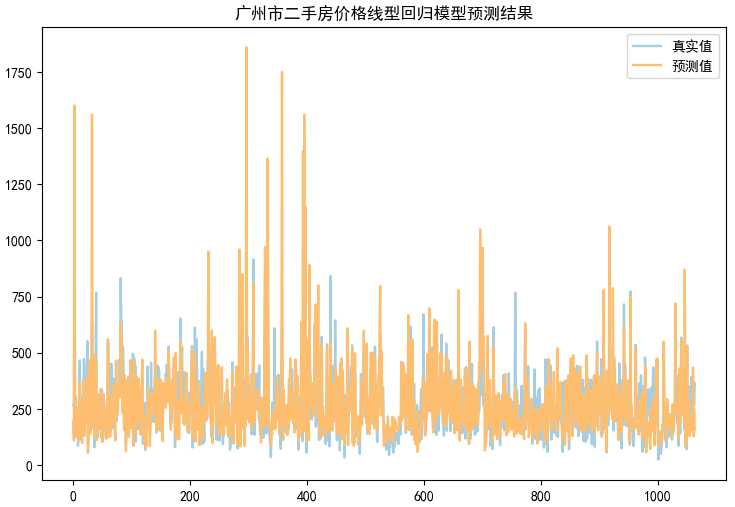
　　 我们可以看到预测值和真实值还是比较接近的，这说明用单价来预测总价还是比较靠谱的。从模型的权值也可以看出，预测结果相对准确：

　　                 

import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv(‘house.csv‘, index_col=0)  # 读取数据

# 线型回归
from sklearn.linear_model import LinearRegression

regr = LinearRegression()  # 构建模型
regr.fit(data[[‘单价‘]].values, data[‘总价‘])
print(‘权值：‘, regr.coef_, ‘截距：‘, regr.intercept_)
plt.plot(regr.predict(data[[‘单价‘]].values), linewidth=1.7, linestyle=‘-‘, color=‘#A6CEE3‘)  # 预测结果
plt.plot(data[[‘总价‘]].values, linewidth=1.7, linestyle=‘-‘, c=‘#FDBF6F‘)

# 可视化处理
plt.rcParams[‘font.sans-serif‘] = ‘SimHei‘
plt.rcParams[‘axes.unicode_minus‘] = False
plt.legend([‘真实值‘, ‘预测值‘])
plt.title(‘广州市二手房价格线型回归模型预测结果‘)
plt.show()

　　我们也可以画出单价和总价呈线性关系的可视化视图：

　　　　　　

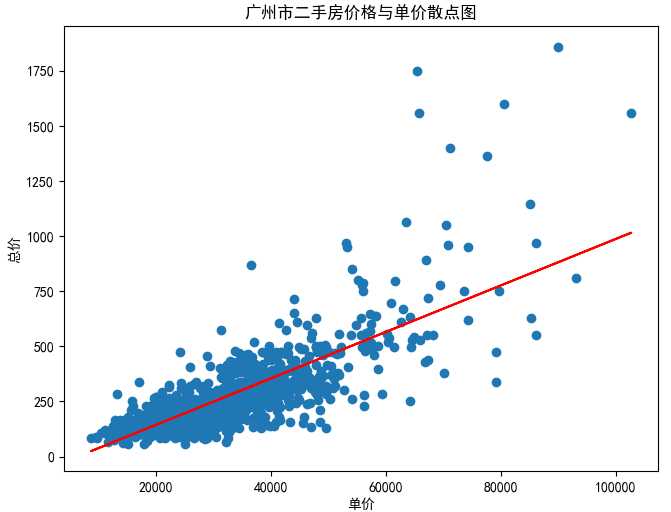
plt.scatter(data[‘单价‘].values, data[‘总价‘].values)
plt.plot(data[[‘单价‘]].values, regr.predict(data[[‘单价‘]].values), c=‘r‘)
plt.title(‘广州市二手房价格与单价散点图‘)
plt.xlabel(‘单价‘)
plt.ylabel(‘总价‘)
plt.show()