算法-基础和查找-1.汉诺塔/2.顺序查找/3.二分查找/4.顺序查找和二分查找的比较

Posted 2021-01-30 mumupa0824

1.汉诺塔：

　　如下图所示，需要将A柱子中的所有圆盘按照从小到大的顺序移动到C柱子上，并且在移动过程中大圆盘不能在小圆盘上面

　　

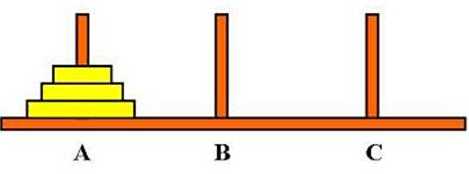
　　分析问题：最终希望呈现的结果是将A柱子上的盘子全部按照从小到大的顺序移动到C柱子上

　　　　1.n个盘子，将n-1视为一个整体

　　　　2.将n-1个盘子视为一个盘子从a经过c移动到b

　　　　3.将n从a移动到c

　　　　4.将n-1个盘子从b经过a移动到c

　　　　5.结束条件：n>0

　　代码如下：

1 def hanoi(n, a, b, c):
2     if n > 0:
3         hanoi(n-1, a, c, b)
4         print("move from %s to %s" %(a,c))
5         hanoi(n-1, b, a, c)
6 
7 hanoi(3, ‘A‘, ‘B‘, ‘C‘)

hanoi

 

2.顺序查找：

　　问题分析：在一个列表中查找一个元素，从头开始，找到了返回索引值，找不到返回None或-1

　　代码如下：

1 def linear_search(li,val):
2     for index,v in enumerate(li):
3         if v == val:
4             return index
5     else:
6         return None
7 
8 print(linear_search([2,3,4],4))

linear_search

 

3.二分查找：　　　

　　问题分析：在一个列表中查找一个元素，每次通过中间位置的数值进行查找　

　　　　1.确定左右的索引，left，right
　　　　2.找到中间位置索引，mid = (left+right)//2
　　　　3.判断中间索引位置的值和待查找的值的大小
　　　　　　1.如果相等，则找到，然会返回索引mid
　　　　　　2.如果索引位置的值大于待查找的值，说明待查找的值在mid左侧，右索引移动到mid前面的位置
　　　　　　3.如果索引位置的值小于待查找的值，说明待查找的值在mid右侧，左索引移动到mid后面的位置
　　　　4.上述步骤成立的前提是左索引需要要小于等于右索引，否则返回None

　　代码如下：

 1 def binary_search(li,val):
 2     left = 0
 3     right = len(li) - 1
 4     while left <= right:    # 候选区有值
 5         mid = (left + right) // 2
 6         if li[mid] == val:
 7             return mid
 8         elif li[mid] > val:  # 待查找的值在mid左侧
 9             right = mid - 1
10         else:  # li[mid] < val 待查找的值在mid右侧
11             left = mid + 1
12     else:
13         return None
14 
15 print(binary_search([1,2,3,5,6,8,9],5))

binary_search

 

4.顺序查找和二分查找的比较：　　

　　时间复杂度:
　　　　顺序查找的时间复杂度为O(n)
　　　　二分查找的时间复杂度为O(logn)

　　测试两种查找方式代码运行的时间，引入一个时间测试模块cal_time如下：

 1 # -*- coding:utf-8 -*-
 2 
 3 # 计算时间函数
 4 
 5 import time
 6 
 7 def cal_time(func):
 8     def wrapper(*args,**kwargs):
 9         t1 = time.time()
10         result = func(*args,**kwargs)
11         t2 = time.time()
12         print("%s running time: %s secs." % (func.__name__,t2 - t1))
13     return wrapper

cal_time

　　测试代码：

 1 # -*- coding:utf-8 -*-
 2 from cal_time import *
 3 
 4 ‘‘‘
 5 时间复杂度:
 6 顺序查找的时间复杂度为O(n)
 7 二分查找的时间复杂度为O(logn)
 8 
 9 ‘‘‘
10 
11 @cal_time
12 def linear_search(li,val):
13     for index,v in enumerate(li):
14         if v == val:
15             return index
16     else:
17         return None
18 
19 @cal_time
20 def binary_search(li,val):
21     left = 0
22     right = len(li) - 1
23     while left <= right:    # 候选区有值
24         mid = (left + right) // 2
25         if li[mid] == val:
26             return mid
27         elif li[mid] > val:  # 待查找的值在mid左侧
28             right = mid - 1
29         else:  # li[mid] < val 待查找的值在mid右侧
30             left = mid + 1
31     else:
32         return None
33 
34 li = list(range(1000000))
35 linear_search(li,389000)
36 binary_search(li,389000)

test_time