三维装箱基于matlab遗传算法求解三维装箱优化问题含Matlab源码 2415期

Posted 2023-03-10 海神之光

⛄一、三维装箱简介

1 引言
三维装箱问题广泛存在于商品的包装、装载、运输之中,特别是在集装箱装载货物方面起着重要的作用。三维装箱问题是一个具有复杂约束条件的组合优化问题,在理论上属于NP hard问题,在实际中更有许多约束条件需要考虑,因此复杂性和难度大。目前国内较好的装箱软件几乎寥寥无几[1]。

集装箱装载问题是:将一批待布箱体(长方体)装入长方体容器中,目标是使容器空间利用率和重量利用率达到最高;同时要考虑到的约束有:箱体本身的承重性、易碎性、箱体搬运的难易、一些货物必须隔离、不允许超过最大承重量、重心与几何形心偏差不应太大、货物码放的稳定性等等。由于存在多目标、多约束的空间规划问题的计算复杂性,利用数学规划法和图论法不太有效,A启发式方法虽然较为有效,但大多只能解一类问题,局限性较大[2]。因此,开发实用的综合考虑多种约束、多种目标的集装箱空间规划算法有待于进一步加以研究。

遗传算法作为一种随机化搜索算法,具有很强的全局搜索能力,比较适合求解集装箱装载问题,目前以遗传算法为基础并加以改进,可以成为解决集装箱问题的可行思路[3]。本文针对具有多目标约束的装箱问题,在单一集装箱装箱算法的基础上,提出了一种适用于多集装箱的启发式混合遗传算法,并对算法的交叉算子和变异算子进行了自适应的改进,经过测试本程序得到的装载计划已经远远超过了人工制定的装载计划,能够给具有装箱业务的企业带来优势。

2 算法的详细设计
本文在遗传算法的基础上结合传统启发式装箱算法,设计成一个混合遗传算法。该算法既继承遗传算法的全局搜索好的优点,也克服了遗传算法局部搜索能力差的缺点,能够较好地解决集装箱这类多目标多约束的空间三维分布的问题。其主要思想是:在整个装箱过程中,将产生的子空间按照容积从小到大进行排序;对某一物品,它总是装到第一个能装下它的箱子中;装完一个物品后,将根据这个物品产生上、左、前3个子空间,如果子空间容积不小于剩余物品的最小体积,则将子空间按容积从小到大重新排序,否则作为空隙排除。这样的装箱方案既符合最佳适应近似算法的思想,同时,物品对空间的分割方式采用三叉树分割法,可以保证货物的边没有悬空现象。

在上述算法的基础上,货物的序号被排列成一个序列作为遗传个体的基因,由遗传群体对基因群体进行变异、交叉等演绎,并按一定规则产生下一代。当遗传的代数足够大的时候,遗传群体中的几个最优遗传个体就可以被近似地当作指定装箱问题的最优解。

基本遗传算法可定义为一个八元组[4]
式中:C为个体的编码方法;E为个体适应度评价函数;P0为初始群体;M为群体大小;!为选择算子;"为交叉算子;#为变异算子;T为遗传运算终止条件。

遗传算法的基本步骤:确定编码方案、确定适应函数、确定选择策略、控制参数的选取、遗传算子的设计、算法终止准则的确定等。

2.1 编码设计
遗传算法的操作对象(计算矩阵)是基因。这个基因代表的就是一个遗传群体中的个体,具体到装载问题中就是装载计划,装载计划是三维空间中货物的分布。因此,如何把三维空间的货物分布解释为数字串和如何把数字串解释为三维空间的货物分布是本算法必须首先解决的问题。

平面布局一般采用待布物体在平面上的坐标组成解串。但是,坐标值的调整变化仅描述了待布物本身位置的改变,可能会使待布物之间出现干涉,为此需要进行判断,以避免出现干涉,亦即坐标值的变化是受限制的。这不适合于用遗传算法求解,而且在三维空间布局中,干涉的计算量要大得多,因此需要构造一种新的、更适合的表示方式。

把待布物的编号按排放顺序排列成染色体,即

p=p1,p2,p3,…,pn

其中n表示待布物的个数,pi为整数,其值代表盒子的编号。交叉和变异算子对其进行的操作实际上就是改变待布物的排放顺序,从而产生不同的空间规划图(不同的解)。染色体P是解的基因型表示,能否简单、快速地将其转化为表现型(空间规划图)从而求出其有关评价参数,就成为遗传算法能否有效应用的关键。采用如下译码算法。

布局空间分解过程采用三叉树数据结构表示。先对原始布局空间求解,此时原始布局空间为当前布局空间,对应于三叉树的根结点。染色体P的先后顺序,从可选布局物体中选择一个相对于当前布局空间为最优的布局物体,其摆放方式通过可行域的形状确定。将其定位于当前布局空间后部的左下角,如图1位置所示,并将布入的物体编号从P中删除。这样,原布局空间的剩余空间可分为L,M,R这3个子空间,分别对应于三叉树根结点的左、中、右3个子结点,剩余的布局空间就变成3个独立的布局空间。依次将L、M、R当作当前空间,对3个布局空间重复上述分解过程,直至没有待布局物体满足要求或集装箱没有可利用空间时停止。

这样,染色体P就转化为布局图,并且克服了空间干涉约束。由此可见,三叉树结构对于求解复杂集装箱布局的空间分解问题有着明显的优势,但对于具有特殊形状的容器的布局问题,目前还无法很好地应用。

2.2 适应度函数
遗传算法对一个解的好坏用适宜度函数值的大小来评价,适宜度的值越大,解的质量越好。在讨论遗传算法的实现之前,应先定义适宜度函数。评价一个解的好坏需要考虑以下几个方面:

(1)空间利用率函数

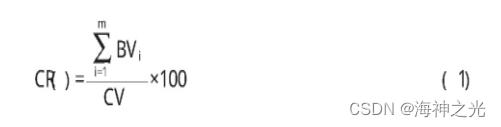
BVi表示第i个布入的盒子的体积,CV表示集装箱体积,m为布入的盒子数。

(2)重量考察函数

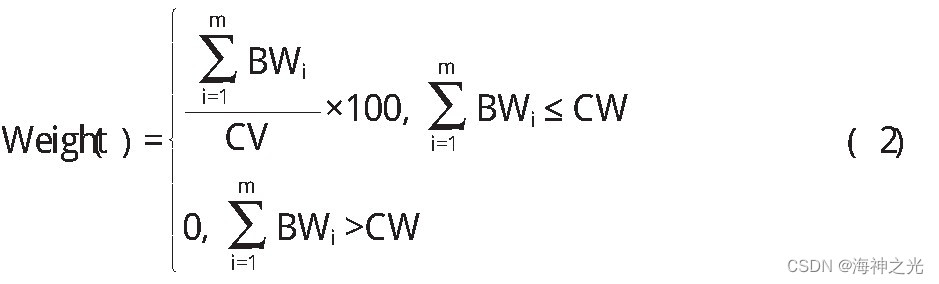
BWi表示第i个布入盒子的质量,CW表示集装箱最大承载重量。超过最大重量,惩罚Weight()为0。

(3)重心考察函数

CH表示集装箱高度,表示第i个盒子的重心高度,通常取盒子高度的一半,表示第i个盒子的重心。该函数主要考察码放的稳定性和搬运的难易性。若重物体都在下面,则码放稳定,且易搬运。

因此,根据惩罚函数法和处理多目标优化的加权系数法。定义适宜度函数为

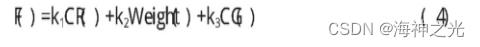
k1、k2、k3为权重,根据经验来选择。

2.3 遗传算子设计
(1)选择算子

本文采用比例选择法和最优保存策略,既能保证适应度较高的个体遗传到下一代,又能保证有较高的全局收敛性。最优保存策略可视为选择操作的一部分,该策略的实施可保证迄今为止所得的最优个体不被交叉、变异等遗传运算所破坏,它是遗传算法以概率1收敛到全局最优解的一个重要保证条件。

(2)变异算子

在传统遗传算法中变异就是以一定的概率随机改变基因。

由于装箱问题的特殊性,变异算子与传统的遗传算法变异有些区别。因为在装箱问题中,遗传基因的一个节点被表示为一个货物的序号,显然如果随机的改变基因,而没有一定的约束,将会导致每种货物的数量发生改变,从而改变了整个问题的问题空间,而导致谬误。

因此本文采用如下变异操作,以较小的概率pm对数字串P中任意两个基因座p和q之间的基因进行逆排列。这样基因的变异实际上是改变货物在装箱队列中的位置,整个变异过程更加接近于一个个体与其本身的一种交叉。

(3)交叉算子

对于本文这种类似于旅行商的以符号编码的基因串P,交叉方式有部分映射交叉、顺序交叉、循环交叉等。本文采用部分映射交叉方式。

部分映射交叉也称为部分匹配交叉,这种交叉操作的主要思想是:整个交叉操作过程由两步来完成,首先对个体编码串进行常规的双点交叉操作,然后根据交叉区域内各个基因值之间的映射关系来修改交叉区域之外的各个基因座的基因值。

在计算出各个个体的适应度以后,算法把装箱方案数据(个体)和适应度数据交付给“个体优胜劣汰”过程。该过程模拟了自然界个体之间的互相竞争过程,通过该过程,适应度好的个体被尽量保存下来,而适应度差的个体则很大程度上被淘汰出局。

由于参照这个适应度趋势对群体交叉、变异的参数进行了调整,实际上算法模拟了某种近似于退火的过程,从解空间上来说,这种做法使得遗传群体的搜索范围和步径能够随着解空间的变化而变化,所得到的实际上是一个“自适应”的遗传算法,克服了传统遗传算法的早熟和欺骗的缺陷。

⛄二、部分源代码

% 使用遗传算法得到最大装载方式
%　定义初始种群为100个
% 交叉方式为两两交叉组合，分裂概率为0.7
% 变异方式为随机变异，变异概率为0.3
% 然后进行选择 选择前面最优的100个

rateCom=0.7;%结合概率
rateAbe=0.3;%变异概率
populations=10;%种群大小
Maxtime=10;%最大迭代时间
%BigSet = zeros(80,3);
%for i = 1:80
% BigSet(i,:)=[randi([30,40]),randi([25,30]),randi([20,25])]*0.01;
%end

BigSet=[1,1,1,100; 2,2,2,100];% 表示可用箱子，前三个属性表示箱子三维尺寸，第四个属性为箱子数量
xscale=10;
yscale=10;
zscale=10;%箱子尺寸限制

%----使用遗传算法-----%
%xscale 表示容器x长度
%yscale 表示容器y长度
%zscale 表示容器z长度
%SolutionPosition 物体摆放点（左前下角）
%SolutionQ 物体摆放种类
%SolutionD 物体摆放方向
%SolutionV 物体体积
[SolutionQ,SolutionD,SolutionPosition,SolutionV]…
=Genetic(rateCom,rateAbe,populations,BigSet,xscale,yscale,zscale,Maxtime);

%根据得到的位置序列，对应的物体种类、物体方向进行绘图
plotPermute(SolutionPosition,SolutionQ,SolutionD,BigSet);

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]江宝钏,熊伟清.一种求解三维集装箱装箱问题的混合遗传算法[J].计算机工程与应用. 2007(26)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除