二维装箱基于matlab遗传算法求解矩形地块二维装箱放置优化问题含Matlab源码 1556期

Posted 2021-12-24 紫极神光

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源： 【二维装箱】基于matlab遗传算法求解矩形地块二维装箱放置优化问题【含Matlab源码 1556期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、二维装箱简介

１ 引言
二维装箱问题是随着计算机技术的产生而出现的，大量出现 在 机 械 制 造、皮革服装加 工、汽车、造船、货物装载以及大规模集成电路板的设计等领域。排样布局的优劣直接与材料的成本及经济效益相关。目前主要存在的问题是材料的利用率偏低，造成巨大的浪费。对于规模较大的生产厂家来说，即使是材料利用率有很小的提升，也会带来巨大的经济效益。
根据目标的不同，二维装箱问题可以分为以下几类：箱柜装载问题（ｂｉｎｐａｃｋｉｎｇｐｒｏｂｌｅｍ）：给定一些不同类型的矩形箱子和一些规格一致的矩形容器，问题是要把所有箱子装入最少数量的容器中。
容 器 装 载 问 题 （ｃｏｎｔａｉｎｅｒｐａｃｋｉｎｇｐｒｏｂ－ｌｅｍ）：所有箱子要装入一个宽度为有限数值的矩形容器，它的高度不限，要求将所有物品放入容器中，
并取得最小的放置高度，使容器利用率最高。 · 背包装载 问 题（ｋｎａｐｓａｃｋｌｏａｄｉｎｇｐｒｏｂ－ｌｅｍ）：每个箱子有一定的价值，背包装载是选择箱子的一部分装入容器中，使得装入容器中的箱子总价值最大。
本文主要研究第二类装箱问题。目前提出的基于遗传算法的装箱算法主要有ＢＬ（ｂｏｔｔｏｍｌｅｆｔ）算法、下台阶算法、最低水平线算法和基于最低水平线的搜索算法。其中下台阶算法是在 ＢＬ算法的基础上的改进，最低水平线算法又在此基础上改进，基于最低水平线的搜索算法则是在最低水平线算法基础上又提出的改进。本文提出一种新的排列方法，通过对多组实验结果进行测试比较，证明了本文算法的有效性。

２ 问题描述
对于所要研究的二维装箱问题，可作如下抽象：给定一个矩形容器Ａ，其宽度和高度分别为 Ｗ 和Ｈ。另有ｎ 个 矩 形 物 块，其宽度和高度分别为ｗｉ，ｈｉ（ｉ＝１，２，…，ｎ）。确定排列方案，将所有物块放入矩形箱子，并使其所占用的空间最小。
排列过程中须满足以下要求： １）放入的任意物块的任意部分均不超出箱子边界。２）任意两个物块的任意部分互不重叠。

３ 装箱算法
在人工排列的过程中，为了使物块占用的空间最小，我们总是试图将物块放置在尽可能 低，且尽可能靠左的位置。在将物块放得尽可能低的过程中，物块最终会受到之前放入的物块的上边缘或是箱子底面边界的阻 挡。在将物块放得尽可能靠左的过程中，物块最终也会受到之前放入的物块的右侧边缘或是箱子左侧边界的阻挡。作为物块的左侧边与下侧边的交点，其左下角点在放置过程中会同时受到之前放入的物块的上边缘或是箱子底面边界和之前放入的物块的右边缘或是箱子左侧边界的阻挡。所以在放置物块的过程中，会以其左下角点作为参考点（ｒｅｆｅｒｅｎｃｅｐｏｉｎｔ）。

3.1 可放置点
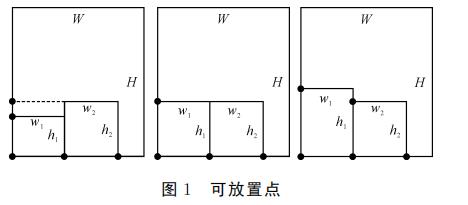
以箱子的左下角点为原点，以箱子的底边为ｘ轴，以箱子左侧边为ｙ 轴。在放入第一个物块时，坐标原点为坐标系中唯一的可放置点 （ａｖａｉｌａｂｌｅｐｏｉｎｔ）。在放入第一个物块之后，位于坐标原点的可放置点被占用，同时在物块的右下角点和左上角点产生两个新的可 放 置 点。第一个放入的物块的宽度和高度分别为 ｗ１和ｈ１，则产生的两个可放置点坐标为（ｗ１，０）、（０，ｈ１）。假设第二个箱子占用了点（ｗ１，０），则删除（ｗ１，０）点，同时增加因物块的右侧面而产生的可放置点（ｗ１＋ｗ２，０）。至于物块的上侧面产生的可放置点，应当有以下几种情况： １）如果ｈ２＞ｈ１，则产生可放置点（０，ｈ２）；
２）如果ｈ２ ＝ｈ１，则产生的可放置点与第一个物块产生的可放置点（０，ｈ１）重合； ３）如果ｈ２＜ｈ１，则产生可放置点（ｗ１，ｈ２）。
从放置过程中可以看出，在放入一个物块的过程中，占用了一个可放置点，同时最多增加二个可放置点。因此，考虑第ｉ个箱子时，最多有ｉ个可放置点。而在实际操作过程中我们发现，由于重叠等情况的出现，可放置点通常会少于ｉ个。

3.2 可放置空间
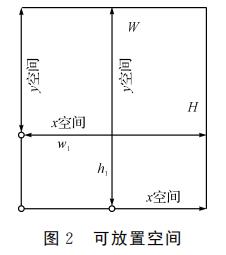
为了将物块放入某个可放置点，需要该点在ｘ轴方向和ｙ轴方向有足够的空间，至少能够容纳物块的宽度和高度。 将ｘ轴方向的可放置空 间（ａｖａｉｌａｂｌｅｓｐａｃｅ）称为ｘ空间，将ｙ轴方向的可放置空间称为ｙ 空间。一般情况下ｘ空间为从可放置点的横坐标开始，一直向右延伸直到接触到已放入物块的侧面或是箱子的壁为止的这段距离。同样，ｙ空间为从可放置点的纵坐标开始，一 直向上延伸直到接触到已放入物块的底面或是箱子的壁为止的这段距离。
在得到了可放置空间之后，物块的放置过程就变成了简单的排序与比较过程，不需要将物块放入某个可放置点，就能检验其是否合适放入该点。极大地简化了计算过程，提高了计算速度。

３.３ 可放置点的刷新
在放入一个新的物块之后，会产生新的可放置点，这就需要对可放置点的集合进行刷新。同时在放入物块的过程中，有些可放置点虽然没有被占用，但会被物块覆盖，这种情况下就需要对可放置点的坐标进行调整。对可放置点进行调整的过程中，也需要对可放置 空 间进行调整，这个过程称为可放置点的刷新（ｒｅｎｏｖａｔｉｏｎｏｆａｖａｉｌａｂｌｅｐｏｉｎｔｓ）。尤其需要说明的是，可放置点不会因为被覆盖或是被阻挡而删除，只是其ｘ坐标或是ｙ坐标以及ｘ空间或是ｙ空间会受到影响。可放置点只会因为以下几种原因被删除： １）被放入的物块占用； ２）因放入物块的影响使得可放置点的ｘ 空间小于尚未放入的物块中最小的宽度值，或是可放置点的ｙ空间小于尚未放入的物块中最小的高度值； ３）后放入的物块产生的可放置点与现有的可放置点出现重叠，则删除其中的一个。这样就使一些没有被当前放入的物块利用就被封闭在了一个小空间里，但依然有希望被后续放入的物块利用的可放置点得以保留。这样做可以有效地提高空间的利用率，同时降低对放 置 顺 序 的 敏 感 性，可以更快地接近最优的排列方案。这也是本算法的重要特点。

３.４ 装箱算法
综上，我 们可以得到２Ｄ－ｐａｃｋｉｎｇ 算 法。算法以物块集合Ｂ＝｛ｂ１，ｂ２，…，ｂｎ｝为输入，返回此次排列得到的空间 利 用 率，用ｕｓｅ 表示可放置点的集
合，矩形容器的宽度和高度分别为Ｗ和Ｈ。算法：２Ｄ－ｐａｃｋｉｎｇ（Ｂ）初始可放置点ｕｓｅ＝［０，０，Ｗ，Ｈ］；
Ｆｏｒｉ＝１：ｎ
待放置物块的宽度为 ｗｉ，高度为ｈｉ；
　　ｕｓｅ按ｘ坐标和ｙ 坐标由小到大顺序排列；
　　　ｕｓｅ中有ｍ 个可放置点；
Ｆｏｒｊ＝１：ｍ
　　Ｉｆ第ｊ个可放置点的ｘ 空间ｗｉ且ｙ 空间ｈｉ
　　　返回ｊ
　　Ｅｎｄ
Ｅｎｄ
占用第ｊ个可放置点；
　　计算右侧边产生的可放置点；
　　　计算该点的可放置空间；
　　　　计算上侧面产生的可放置点；
　　　　　计算该点的可放置空间；
　　　　　　将新产生的可放置点放入 ｕｓｅ集合的末尾；
　　Ｆｏｒｋ＝ｒ：－１：１
　　　分别计算对各可放置点及可放置空间的影响；
　　Ｅｎｄ
Ｅｎｄ
　　　计算所有物块的面积和；
　　　　返回所有物块中最大的ｙ坐标；
　　　　计算空间利用率。
在该算法中，初始可放置点为坐标原点，可放置空间为箱子的宽度和高度，按顺序放置每个物块。将所有可放置点分别按ｘ坐标和ｙ坐标由小到大排列，依次检测每个可放置点的ｘ空间和ｙ空间能否容纳将要放入的物块，选择占用第一个满足要求的可放置点。然后计算物块产生的新的可放置点，向可放置点集合中加入新产生的点并删除已经占用的点。计算新放入的物块对其他可放置点及其可放置空间的影响。算法结束时，返回该排列方案对应的空间利用率，即装箱物块的总面积对箱子面积的比率。

４ 遗传算法求解过程
遗传算法的主要运算过程如下：
１）编码：解空间中的解数据ｘ，作为遗传算法的表现型形式。从表现型到基因型的映射称为编码。遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据，这些串结构数据的不同组合就构成了不同的点。在本算法中，将每一种排列方案编码成一个二进制字符串。
２）初始群体的生成：随机产生 Ｎ 个初始串结构数据，每个串结构数据称为一个个体，Ｎ个个体构成了一个群体。遗传算法以这Ｎ个串结构作为初始点开始迭代。设置进化代数计数器ｔ←０；设置最大进化代数 Ｔ；随 机 生 成 Ｍ 个个体作为初始群体Ｐ（０）。
３）适应度值评价检测：适应度函数表明个体或解的优劣性。对于不同的问题，适应度函数的定义方式不同。根据具体问题，计算群体 Ｐ（ｔ）中各个个体的适应度。在本算法中，空间利用率是最重要的适应度评价标准。
４）选择：将选择算子作用于群体。
５）变异：将交叉算子作用于群体。
６）变异：将变异算子作用于群体。
群体Ｐ（ｔ）经过选择、交叉、变异运算后得到下一代群体Ｐ（ｔ＋１）。
７）终止条件判断：若ｔＴ，则ｔ←ｔ＋１，转到步骤２）；若ｔ＞Ｔ，则以进化过程中所得到的具有最大适应度的个体作为最优解输出，终止运算［８～１０］。
遗传算法有三个基本操作：选 择（ｓｅｌｅｃｔｉｏｎ）、交叉（ｃｒｏｓｓｏｖｅｒ）和变异（ｍｕｔａｔｉｏｎ）。
１）选择。选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁殖子孙。根据各个个体的适应度值，按照一定的规则或方法从上一代群体中选择出一些优良的个体遗传到下一代群体 中。遗传算法通过选择运算体现这一思想，进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。这 就 体 现了达尔文的适者生存原则。
２）交叉。交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体，新个体组合了父辈个体的特性。将群体内的各个个体随机搭配成对，对每一个个体，以某个概率交换它们之间的部分染色 体。交叉体现了信息交换的思想。
３）变异。变异操作首先在群体中随机选择一个个体，对于选中的个体以一定的概率随机改变串结构数据汇总某个串的值，即对群体中的每一个个体，以某一概率改变某一个或某一些基因座上的基因值为其他的等位基因。同生物界一样，遗传算法中变异发生的概率 很 低。变异为新个体的产生提供了机会。

三、部分源代码

%%%%%%%%%%%%%%%%遗传算法主程序%%%%%%%%%%%%%%%%%%%%%%%%
clc
clear all
global  data NUM  layout
data=[60 15 100 55 15 6.00
      60 15 100 52 20 5.88
      60 16 100 50 20 6.06
      55 15 100 50 20 5.92
      55 15 100 46 25 5.92
      50 15 100 48 20 5.95
      50 15 100 45 25 5.83
      50 15 100 43 25 6.03
      45 15 100 45 20 6.06
      45 15 100 37 30 6.06
      40 15 100 45 20 5.83
      40 15 100 33 35 5.83
      35 15 100 42 20 5.83
      35 15 100 29 35 5.97
      35 15 100 37 20 6.06
      35 15 100 25 35 6.06
      25 15 100 34 20 5.95
      25 15 100 25 30 5.97
      20 15 100 30 20 5.83
      20 15 100 21 30 5.83];

layout=[3 2 3 2 2 2 2 2 2];
pop=30; %染色体数目
MaxGen=100; %迭代次数
N=NUM*2;%变量个数
Pc=0.75; %交叉概率
Pm=0.05; %变异概率
%产生初始种群
Chrom=zeros(pop,N);
TempChrom=Chrom;
J=zeros(pop,1);
J1=zeros(pop,1);
for i=1:pop
   Chrom(i,1:NUM)=randperm(NUM);
   for j=1:NUM
       Chrom(i,j+NUM)=randi([1,layout(j)],1,1);
   end
   [val,rou]=objection(Chrom(i,:));%求当前种群个体的目标函数值
   J(i)=val;
end
hwait=waitbar(0,'please wait............');
steps=MaxGen;
Jlist=zeros(MaxGen,1);
%开始迭代求解
for k =1:MaxGen
 total_obj=sum(J);
 Fit0=J;%取当前个体目标函数值为适应度值              
 totalfit =sum(Fit0);
 fitvalue =cumsum(Fit0);%累计值
%轮盘赌选择优秀个体

%遗传操作
 for i =1:2:(pop-1)
    if Pc>rand 
           m=randi([2,NUM-1],1,2);
           Min=min(m);
           Max=max(m);
           TempPart1=TempChrom(i,1:NUM);
           TempPart2=TempChrom(i+1,1:NUM);
           Temp=TempPart1(1:Min-1);
           TempPart1(1:Min-1)=TempPart2(1:Min-1);
           TempPart2(1:Min-1)=Temp;   
              
           Temp1=TempPart1(Max+1:NUM);
           TempPart1(Max+1:NUM)=TempPart2(Max+1:NUM);
           TempPart2(Max+1:NUM)=Temp1;
           for j=1:Min-1
               while(find(TempPart1(Min:Max)==TempPart1(j)))            
                 temp0=find(TempPart1(Min:Max)==TempPart1(j));
                 TempPart1(j)= TempPart2(temp0+Min-1);
               end

               while(find(TempPart2(Min:Max)==TempPart2(j)))             
                 temp1=find(TempPart2(Min:Max)==TempPart2(j));
                 TempPart2(j)=TempPart1(temp1+Min-1);
               end
           end
                         
           for j1=Max+1:NUM
               while(find(TempPart1(Min:Max)==TempPart1(j1)))            
                 temp2=find(TempPart1(Min:Max)==TempPart1(j1));
                 TempPart1(j1)=TempPart2(temp2+Min-1);
               end 
              
               while(find(TempPart2(Min:Max)==TempPart2(j1)))             
                temp3=find(TempPart2(Min:Max)==TempPart2(j1));
                 TempPart2(j1)= TempPart1(temp3+Min-1);
               end
           end
           
           TempPart11=TempChrom(i,1+NUM:N);
           TempPart22=TempChrom(i+1,1+NUM:N);
           alpha=rand(1,NUM);
           Temp11=round(alpha.*TempPart11+(1-alpha).*TempPart22);
           Temp22=round(alpha.*TempPart22+(1-alpha).*TempPart11);
           for jj=1:NUM
               if Temp11(jj)<1
                   Temp11(jj)=1;
               end
               if Temp11(jj)>layout(jj)
                   Temp11(jj)=layout(jj);
               end
               if Temp22(jj)<1
                   Temp22(jj)=1;
               end
               if Temp22(jj)>layout(jj)
                   Temp22(jj)=layout(jj);
               end
           end
           TempChrom(i,:)=[TempPart1,Temp11];
           TempChrom(i+1,:)=[TempPart2,Temp22];
    end
 end
%变异操作
 for i =1:pop
  if Pm>rand
     point=randi([2,NUM],1);
     Temp11=TempChrom(i,1:NUM);
     Temp22=TempChrom(i,1+NUM:N);
     Temp22=layout-Temp22+1;
      for jj=1:NUM
         if Temp22(jj)<1
             Temp22(jj)=1;
         end
         if Temp22(jj)>layout(jj)
             Temp22(jj)=layout(jj);
         end
         if Temp22(jj)<1
             Temp22(jj)=1;
         end
         if Temp22(jj)>layout(jj)
             Temp22(jj)=layout(jj);
         end
      end
     TempChrom(i,:)=[fliplr(Temp11(1:point)) Temp11(point+1:NUM) Temp22];
  end
 end

 end
 [value,ind]=max(J);
 if value>J1(ind)
   TempChrom(ind,:)=Chrom(ind,:);
   J1(ind)=value;
 end
 Chrom=TempChrom;
 J=J1;
 Jlist(k) =value;%记录当前最优值
 str=[num2str(round((k/steps)*100)),'%'];
 waitbar(k/steps,hwait,str);
end
%结果输出
close(hwait);
[BestFit,BestId]=max(J);
Result=Chrom(BestId,:);
[result_val,Order]=objection(Result);
disp(['摆放选择及顺序： ',num2str(Order)]);
disp(['容积率： ',num2str(result_val)]);
%画算法收敛图
figure(1)
plot(1:length(Jlist),Jlist,'r','linewidth',2)
xlabel('迭代次数');
ylabel('每代最优目标函数值');
title('遗传算法收敛图')
% legend('解的变化')

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]田大肥,申喜,周巍.二维装箱问题的遗传算法求解[J].舰船电子工程. 2014,34(01)