船舶基于matlab simulink船舶推力分配含Matlab源码 2416期

Posted 2023-03-10 海神之光

⛄一、船舶推力分配

1 推力分配问题描述
动力定位船舶为了始终稳定在海平面上预定的位置，会装备比常规船舶更多种类和数量的推进器。DPS中推进器的数目一般多于五台，意味着对于一组给定的控制力，系统存在很多种不同推力大小和方向的组合。推力分配要解决的问题就是实时进行推力分配，在众多组合中找到最优分配方案[10]。

动力定位控制器通过状态反馈η和v计算船舶达到预定位置所需的推力和扭矩τc，推力分配单元负责将τc转化为各推进器的控制输入α和u，满足如下关系[11]:

每一台推进器对应一个列向量，动力定位船舶三自由度运动控制下，不同类型推进器对应b的表示为

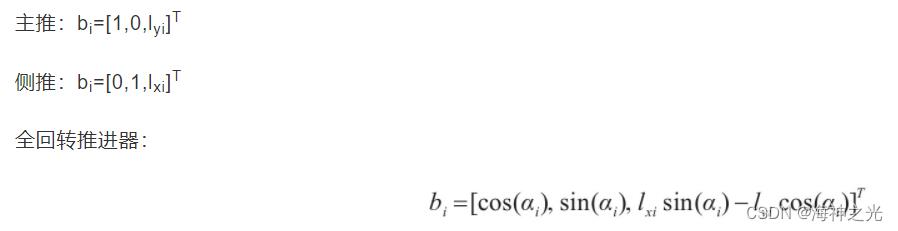
式中，(lxi,lyi)表示第i个推进器在船体坐标系的位置；X为纵轴方向，艏向为正；Y为横轴方向，右舷为正。

推力分配问题中在建立目标函数时，一般会考虑的因素有能耗、误差及推进器方位变化率等。综合各方面因素考虑，目前相关研究中考虑因素最多的目标函数为

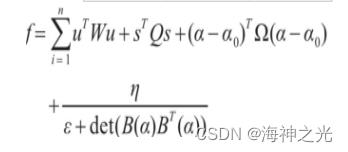
式中，第一项为消耗的总功率；第二项为惩罚项，用来控制要求推力和实际分配推力之间的误差s,Q为正定对角矩阵；第三项为限定全回转推进器方位频繁变化，减少磨损；Ω为正定对角矩阵；第四项用来避免奇异结构。

2 推力分配优化算法
DPS的推力分配问题根据实际情况的需要，一般会适当忽略部分考虑因素，对上述目标函数进行简化，将问题分为线性无约束分配、线性约束分配和非线性约束分配三大类[12]。针对不同类型的分配问题，相应的优化算法得到广泛的应用，常用的推力优化分配算法有广义逆法、序列二次规划算法、粒子群优化算法等。

广义逆法是广义控制分配中比较常用的算法，其基本思路为仅考虑能耗最低，将上述目标函数仅保留功率消耗项，利用推力误差等式作为限制条件，设计Lagrange函数求解目标函数极值。该算法的优点是方法简单、直接，但在计算过程中可能出现奇异结构，使得解过大而不能应用实际。国内外学者针对算法的缺点对该算法进行了改进，Sørdalen[13]将奇异值分解法引入到推力分配问题广义逆法求解，对推力结构矩阵进行奇异值分解，避免产生奇异结构；徐海祥等[14]针对全回转推进器在进行推力分配时，可能因物理限制存在推力饱和或角度饱和的问题，采用级联广义逆算法，对饱和的推力和角度进行截断处理，保证满足上层控制器的要求。

对于推力分配这类非线性约束问题，序列二次规划（SQP）算法是间接求解该类问题比较有效的手段，由美国数学家Wilson在1963年提出[15]，具有收敛速度快、简单易行等优点，但过分依赖于初始值，存在局部收敛等问题。其基本原理是把推力分配优化问题离散近似成一组等效的凸规划序列，利用Lagrange-Newton法形成迭代关系，最后求得最优解。吴显法等[16]以深海钻井和采油平台为研究对象，采用SQP算法达到降低能耗的目的，避免了奇异结构，提高了系统操纵性；刘鹏等[17]对挖泥船自身配置的推进器系统进行分析，运用SQP算法满足了挖泥船的定位要求。

粒子群优化算法由于需要调节的参数非常少，对算法参数调整比较容易，已被应用到很多领域。该算法是对鸟群寻找食物的行为进行模拟，将寻找最优解的过程比作鸟群寻找食物的过程，在这个过程中，每只鸟都有记忆功能，会记录自身曾经找到的历史最优位置并共享给整个鸟群，对整个鸟群最佳鸟的位置信息和速度信息进行更新，直至迭代结束。该算法的原理比较简单，导致了存在求解精度不高、在规定迭代次数达不到理想收敛精度的问题。尚留宾等[18]针对粒子群优化算法解决动力定位推力分配问题此类易遭遇局部最优、计算时间长等瓶颈，探索不同粒子决策变量对推力分配结果的影响，构建了基于3种不同粒子决策变量的粒子群推力分配算法，提高了推力分配的实时性；李新想等[19]提出了一种以粒子群算法为基础，引入混沌理论和遗传算法中交叉变异策略的混合算法，通过对某铺管船的仿真，证明该算法在兼顾能耗的同时有效降低推进器磨损。

除上述算法外，部分文献资料针对上述算法应用在推力分问题中存在的不足，将算法进行了结合和改进，如多智能体粒子群优化算法、粒子群优化算法与SQP算法相结合等；还引入了其他算法，如遗传算法、偏置推力分配算法等。

⛄二、部分源代码

function result=func4(x,apl0,B)
%%最小推力函数%%
Pc=2;
K=1;
% pbias=200-op;
Q1=diag([10^8 10^8 10^9]);
% s0=[x(5);x(6);x(7)];
% result=Pc*((abs(x(1)))^{(3/2)+(abs(x(2)))}(3/2)+(abs(x(3)))^{(3/2)+(abs(x(4)))}(3/2))+s0’Q1s0;
sta=1000;dlt=10^(-6);omg=diag([1 1 10 10]);
apl=[x(5);x(6);x(7);x(8)];
s0=[x(9);x(10);x(11)];
result=KPc((abs(x(1)))^{(3/2)+(abs(x(2)))}(3/2)+(abs(x(3)))^{(3/2)+(abs(x(4)))}(3/2))+s0’Q1s0+(apl-apl0)‘omg(apl-apl0)+sta/(dlt+det(B*B’));
end

⛄三、运行结果

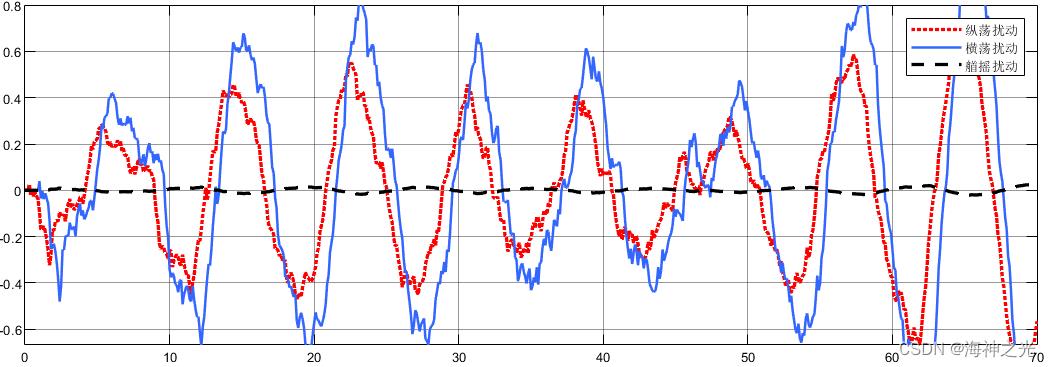
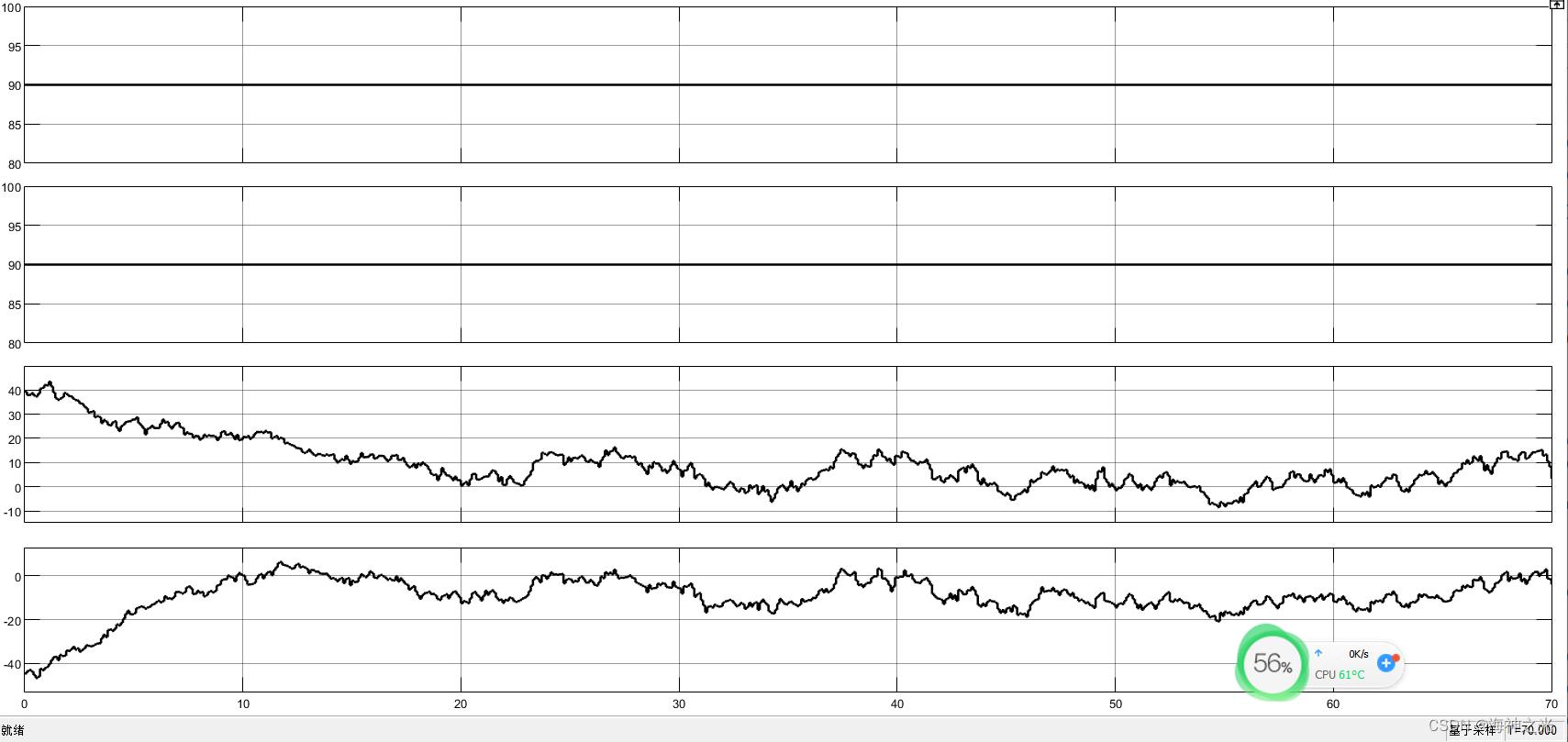
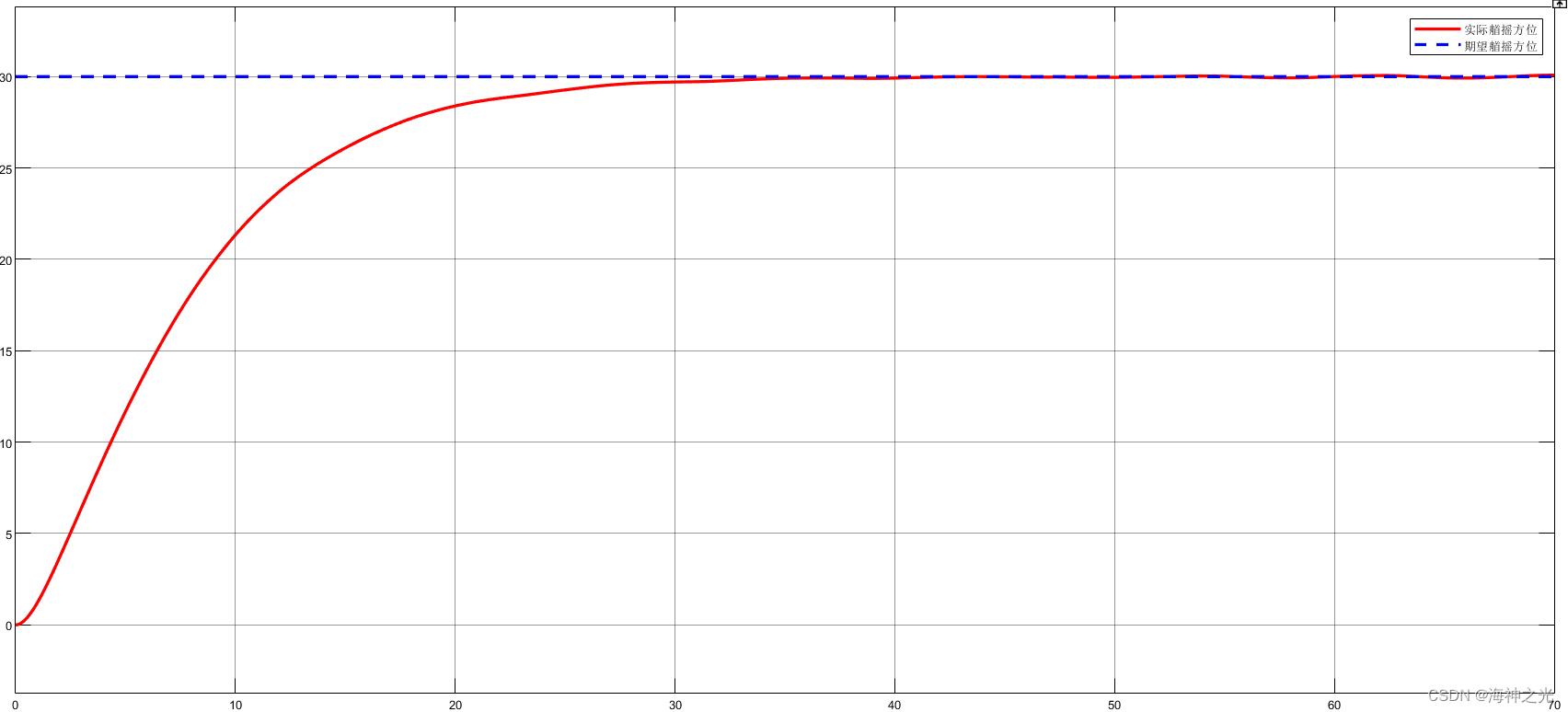
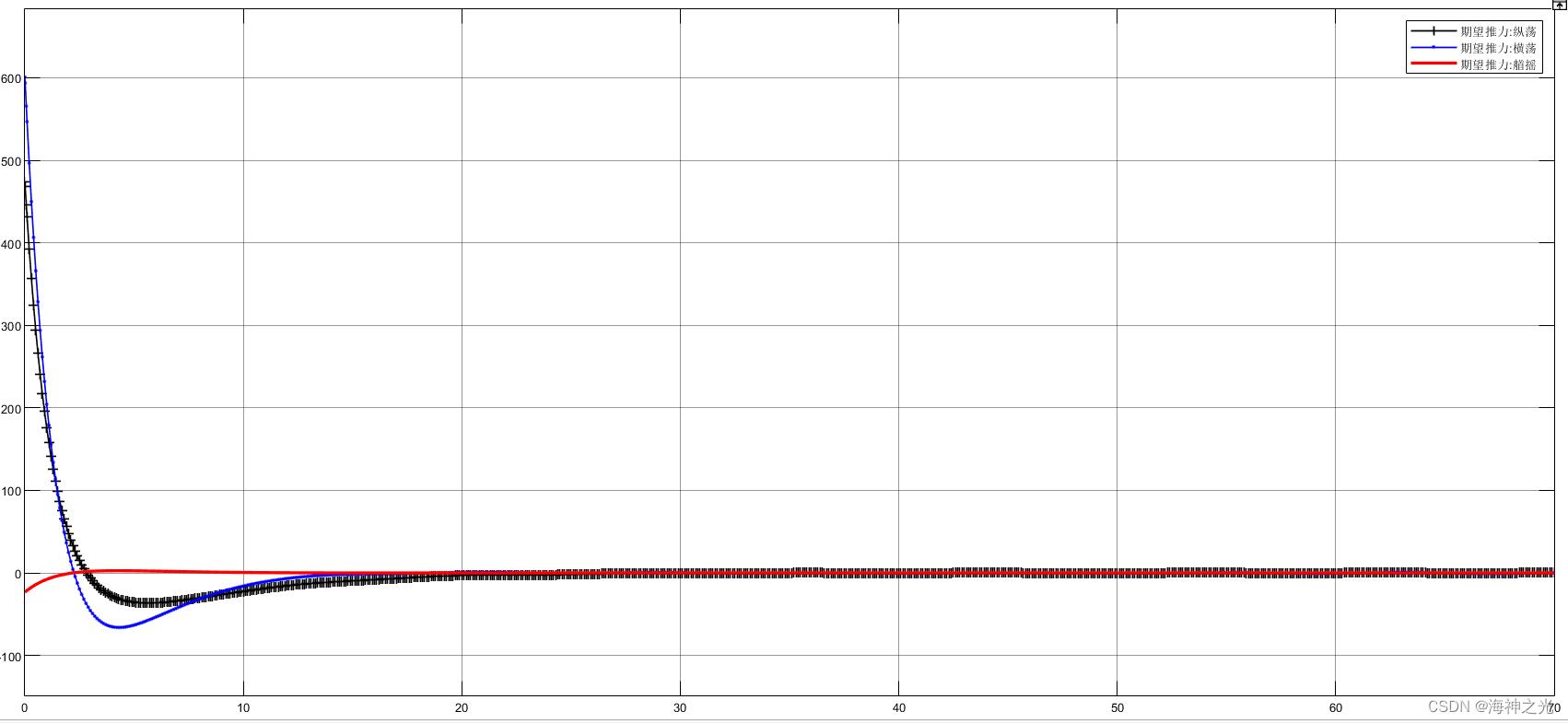
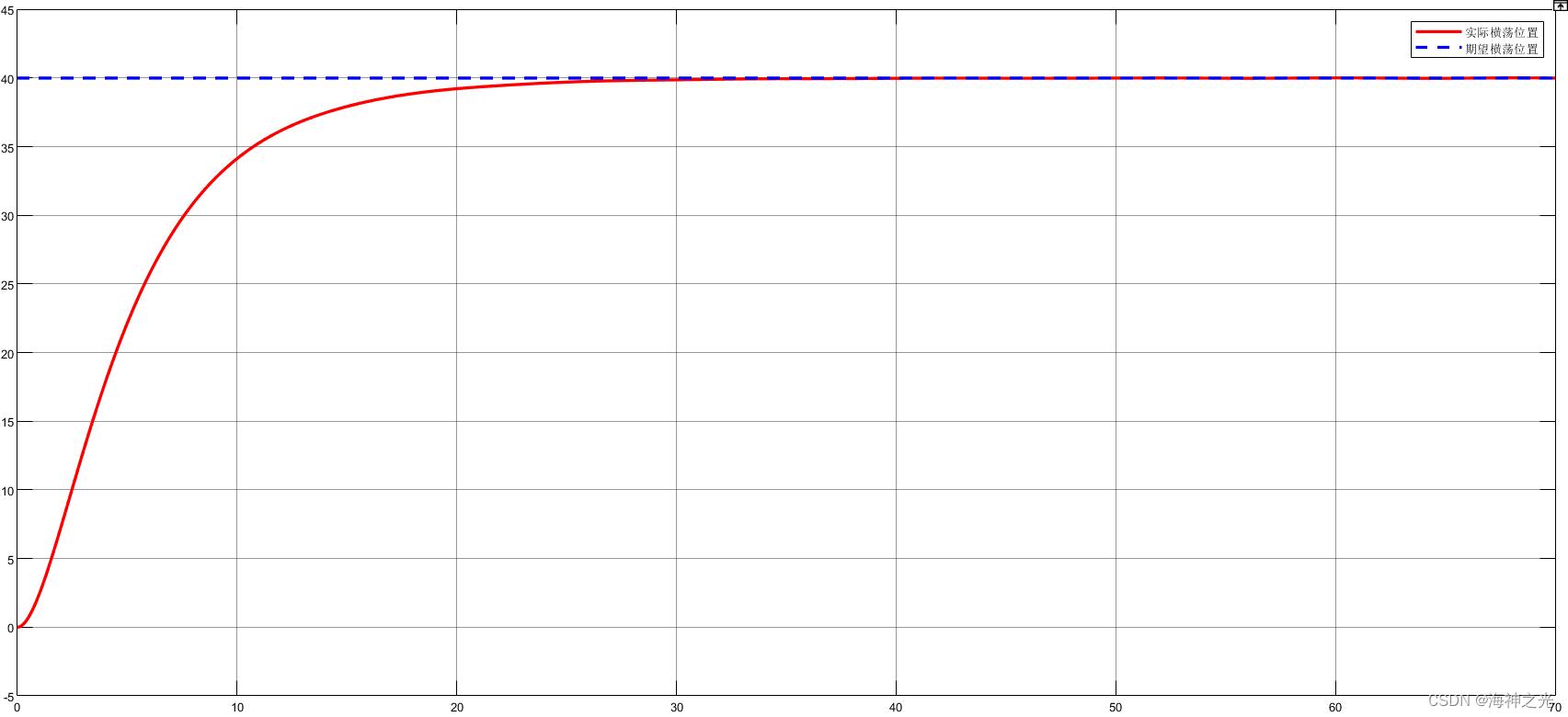
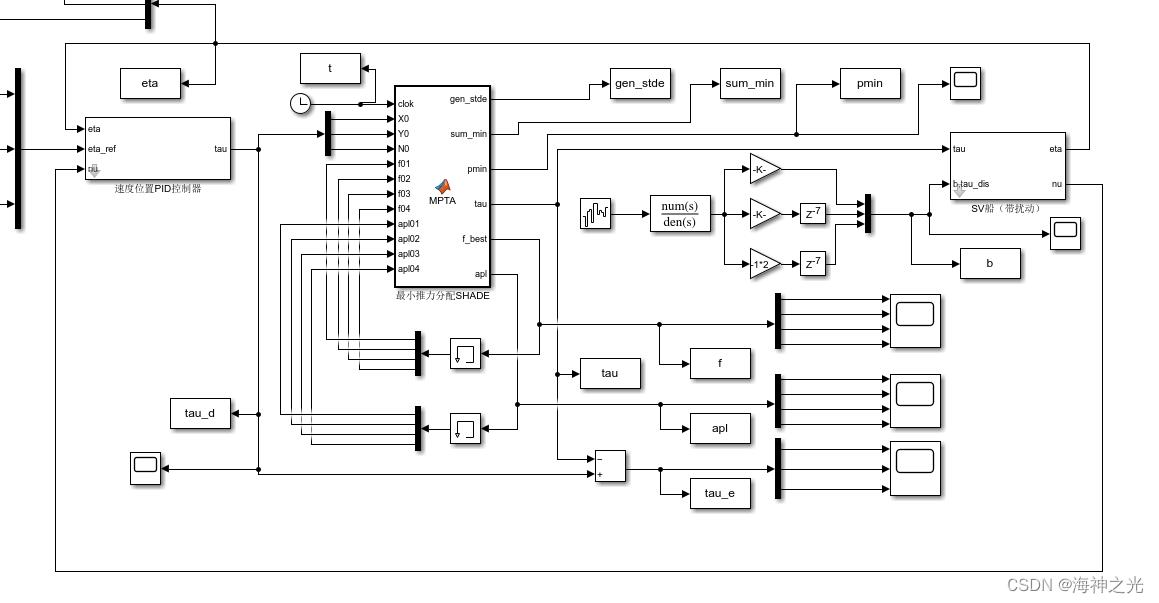
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]曹宇翾,杨宣访,李厚朴.动力定位船舶推力分配问题研究[J].舰船电子工程. 2022,42(10)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除