CF1030D Vasya and Triangle 计算几何构造

Posted 2021-01-25 itst

传送门

---

 

这题竟然只有1700……

我们考虑使用初中学过的割补法求三角形的面积

也就是把一个三角形补成下面这样

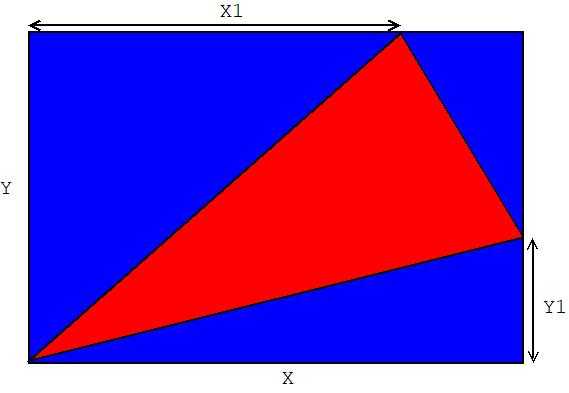
那么三角形的面积$S=XY-frac{(X-X_1)(Y-Y_1)}{2}-frac{XY_1}{2}-frac{X_1Y}{2}=frac{XY-X_1Y_1}{2}$

又因为$X,Y,X_1,Y_1$都是整数，所以三角形的面积里分母的位置只能是$1$或者$2$。我们可以通过$gcd(NM,K)$是否为$K$或$frac{K}{2}$来判断无解。

当我们知道有解了之后，考虑构造方案。

我们令$Y1=1$，$X=N$，那么$S=frac{NY-X_1}{2}=frac{NM}{K}$，也就是说$NY-X_1=frac{2NM}{K}$，那么$Y=lceilfrac{2M}{K} ceil$，$X_1=NY-frac{2NM}{K}$。

#include<bits/stdc++.h>
using namespace std;

int main(){
    long long N , M , K;
    cin >> N >> M >> K;
    if(N * M % K && (K % 2 || N * M % (K / 2))){
        puts("NO");
        return 0;
    }
    puts("YES");
    K = 2 * N * M / K;
    long long L = K / N + (K % N ? 1 : 0) , R = L * N - K;
    cout << "0 0
" << N << " 1
" << R << ‘ ‘ << L;
    return 0;
}