关于网格

Posted 2021-01-23 xuuold

 

网格通常用于游戏中，用于表示游戏区域，如地图（在“文明”和“魔兽”等游戏中），游戏界面（如游泳池，乒乓球和扑克等游戏），运动场（棒球和足球等游戏），棋盘（在象棋，Monopoly和Connect Four等游戏中，以及抽象空间（在俄罗斯方块之类的游戏中）。我试图在这些页面上收集我对网格的看法。我避免实现细节（例如源代码），而是专注于概念和算法。我主要使用网格来表示战略和模拟游戏中的地图。虽然这里的许多概念对各种网格都很有用，但我对这些游戏感兴趣。

网格由重复的简单形状构成。下文将覆盖以下内容：正方形、六边形和三角形，顶点、边和面（平铺的瓦片），坐标系，以及使用网格的算法。

心急的读者可以直接跳到到坐标系。还有一个六边形网格指南，那里有更多的特定于六边形的算法。

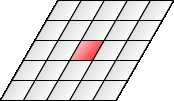
正方形

最常见的网格是方形网格。它简单易用，可以很好地映射到计算机屏幕上。

位置可以使用熟悉的笛卡尔坐标（x，y），轴是正交的。即使您的地图方块在等轴测图或轴测投影中在屏幕上成角度，方形坐标系也是相同的。

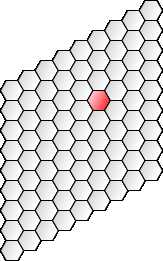
六边形

六边形已经在一些电路板和计算机游戏中使用，因为它们提供的距离失真比方形网格少。这部分是因为每个六边形具有比正方形更多的非对角线邻居。（对角线扭曲了网格距离。）

六角形在自然中存在（蜂窝）并且具有令人愉悦的外观。在本文中，我将使用具有平顶和尖边的六边形，但如果你想要尖顶和平边，数学运算是相同的。

还有一个更全面的指南，涵盖偏移坐标，轴坐标，立方坐标，尖顶，平顶和更多算法。

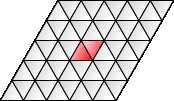
三角形

三角形在3d图形中很常见，但很少用于游戏地图。

它的一大缺点是周长大且面积小（与六边形相反）。小区域意味着将游戏块完全放置在地图上的单个空间内更加困难。

在三维图形中，三角形是唯一的平面形状；正方形和六边形有时可以“弯曲”，有时不可以。

在本文中，我将使用向上和向下指向的三角形，但如果您的三角形指向左右，数学运算也是相同的。

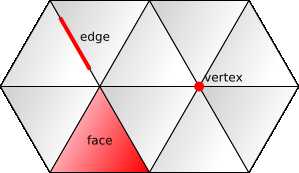
网格部分

网格有三种类型的零件：面（平铺的瓦片）、边和顶点。

每个面都是由边缘包围的二维平面；每个边是一个以两个顶点结束的一维线段；每个顶点都是零维点。

游戏通常只关注这些类型的部分中的一种。

像Chess和Checkers这样的“西方”游戏似乎专注于面，像Go和中国跳棋这样的“东方”游戏似乎专注于顶点。像轮盘赌这样的游戏为所有三种类型的网格部分赋予了意义。

 

面、边和顶点也显示在多边形地图中。

在不需要网格坐标的情况下处理面，边和顶点的算法将适用于这些多边形贴图：

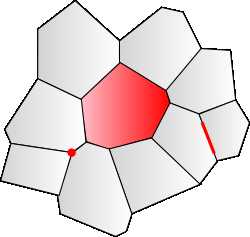
通过将每个面转换为节点，并将面之间的边转换为连接节点的边，可以转换为图的结构，可以使用图论的算法（例如最短路径）。

格图上使用图算法（例如最短路径）。

在游戏中使用

电脑游戏可以使用所有三种网格的零件，但面是最常见的。

建筑物，土地类型（草地，沙漠，砾石等）和领土所有可以使用面。

区域边界和“流动”算法（模拟相邻面之间的水流，人员，货物等）可以使用边。

高度（海拔高度，水深）使用顶点。

道路和铁路可以使用面（如在SimCity中）或边（如Locomotion，请参阅Java小程序演示此内容）。

零件计数

我们可以计算生成网格需要多少面、边和顶点。方法是考虑邻接和共享。

         

 （这段如果看不懂可以往下，推导和坐标系可以辅助理解）

考虑三角形网格。每个三角形面有3个边。因此，边的数量是面的3倍。

但每个边由2个面共享，因此每2个面有3个边。

每个三角面具有3个顶点。每个顶点由6个面共享。因此，我们每6个面有3个顶点，或者每2个面有1个顶点。

在设计坐标系时，这些关系很重要。

正方形具有相同数量的面和顶点。六边形有比面有更多的顶点。三角形有比顶点有更多的面。边的数量总是最多的。

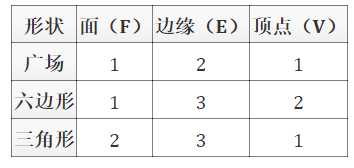
我将这些称为F，E，V计数。正方形的F，E，V是 1, 2, 1；六边形 1, 3, 2；三角形 2, 3, 1。

 

请注意，六边形和三角形网格具有相似的计数，除了顶点和面数计数相反。这是因为六边形网格和三角形网格是成双的：如果将顶点放在三角形网格的每个面的中心，您将获得六边形网格，反之亦然。

方形网格本身就是一致的。如果将顶点放在每个正方形的中心，则会生成另一个正方形网格，与第一个网格偏移。阅读更多维基百科上的密铺的凸多边形。

六边形和三角形网格的推导

六边形和三角形网格可以从方格网格中导出。由于方块的坐标系统很简单，推导之可以指导我们设计六边形和三角形的坐标系。

正方形到六边形

将方形网格转换为六边形网格需要两个步骤。

首先，偏移列（或行）。

其次，取出方形一半的边，在中间弯曲它们进行变形。

 

                                         

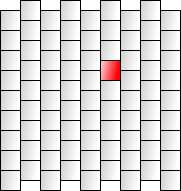
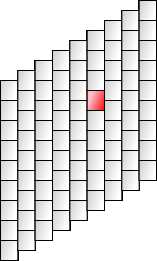
偏移列有两种简单的方法。最常见的是偏移偶数列。

一种更简单的方法是将每列偏移高于前一列的半个高度。使用这种方法的代码更加均匀，但地图形状不再是矩形，这可能不方便。

在这个页面上，我将重点介绍后一种方法；它更容易使用，也可以与三角形一起使用。

                                        

 

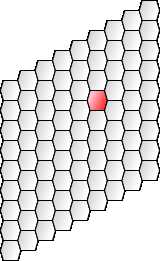
无论采用哪种偏移方法，下一步是分割正方形的垂直的边并弯曲它们。

当弯曲从180度减小到120度时，您将拥有正常的六边形。

 

请注意，分割垂直边意味着我们将边数从4增加到6（每个面净增加1个边，因为2个新边由2个面共享）。

我们还将顶点数从4增加到6（但这些顶点是共享的，因此净增加为1），并且我们保持面的数量不变。

F，E，V计数从1,2,1变为1,3,2。

正方形到三角形

                                        

将方形网格转换为三角形网格需要两个步骤。

首先，我们必须剪切正方形。这给了我们一个菱形网格。

为了制作三角形，我们将每个菱形面分成两个三角形。

拆分每个面意味着我们现在拥有的面数是以前的两倍，我们为每个面添加了1个边，我们没有添加任何顶点。

F，E，V计数从1,2,1变为2,3,1。

坐标系

网格有三个部分（面、边、点），我们需要一种方法来标识它们的每一个。

我将从与网格的轴匹配的简单数字坐标开始。

F，E，V计数告诉我们有多少网格部分共享相同的坐标。

如果多个部分具有相同的坐标，我将使用大写字母来消除歧义。

方形网格

                                        

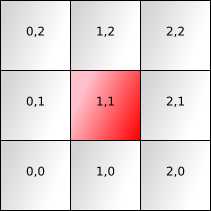
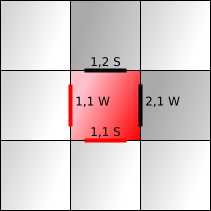
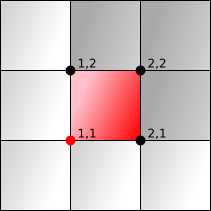
方格很容易。

F，E，V 计数为 1，2，1。这意味着只有边需要一个字母来消除歧义。

对于每个面，我们（任意）指定一个顶点来共享其坐标。我选择了面的西南角。

对于每个面，我们分配两个边来共享其坐标。我选择了南边和西边，并用字母 S和W 标注。

有1个面、2条边和1个顶点共享（1,1）网格坐标。这符合我们的 F，E，V 计数 1，2，1。

六角网格

                                        

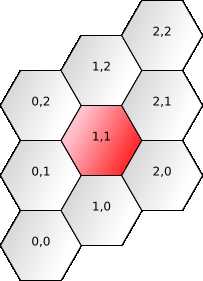
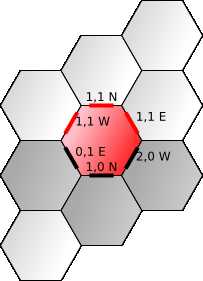
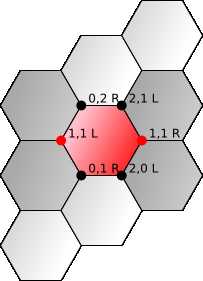
我们用正方形网格创建六边形网格。

六边形面的坐标可以与转换前的正方形面的坐标相同。

 

对于每个面，我们选择三个边和两个顶点来共享相同的坐标。我选择了 NW，N 和 NE 边，并将它们标记为 W，N，E。

我选择了最左边和最右边的顶点，并将它们标记为 L，R。

类似于这样的设定都是可以的。

三角网格                   

        

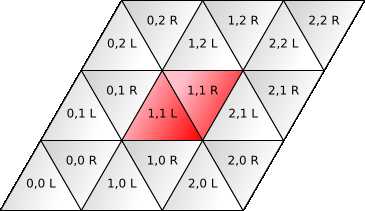
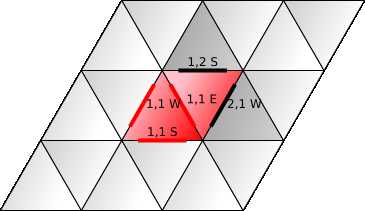
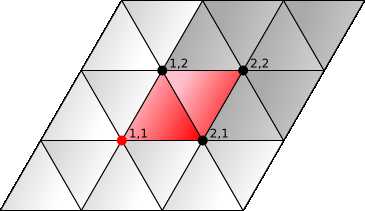
我们用正方形网格创建菱形网格，然后将每个剪切的正方形（菱形）分成两个三角形。

这意味着每个方形面坐标需要分为两个三角形面的坐标。我选择将它们标记为L和R。

边与正方形（W和S）的边相同，除了我们有一个额外的边缘将两个面分裂，将之标记为 E。

额外的三角形面不会创建任何额外的顶点，因此顶点标注与方形网格标注相同。

 

有记载的另一种方案，在这里，我需要学习。它似乎比我在这里更简单。

网格部件之间的关系

 我们可以定义 3 种网格零件之间的关系，从而给出网格之间的 9 种关系。

你可以定义更多的关系，但我会专注于这 9 种。我不知道这些关系的标准名称，所以我已经编写了一些名字。

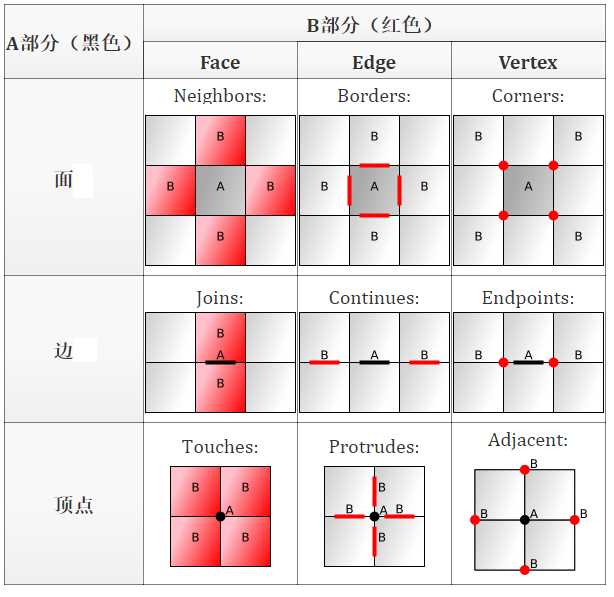
在您的游戏中，您可能想要使用上述变体。

例如，neighbors 和 adjacent 关系可能包括对角线。将 continues 关系可能已包括边缘未用原边共线。我选择了最简单的关系。

算法

 这9个关系中的每一个都可以表示为从A到B列表的算法；我写它们作为A→B1B2B3 ...

有3种形状，因此我们提供了27种可能的算法，这些算法以简单的形式表示，您可以将其转换为您喜欢的编程语言。

对于一些形状和算法，有超过一个A的变体，所以我会列出每个变体的规则。例如，三角形面有L和R变体。

以下是所有算法：

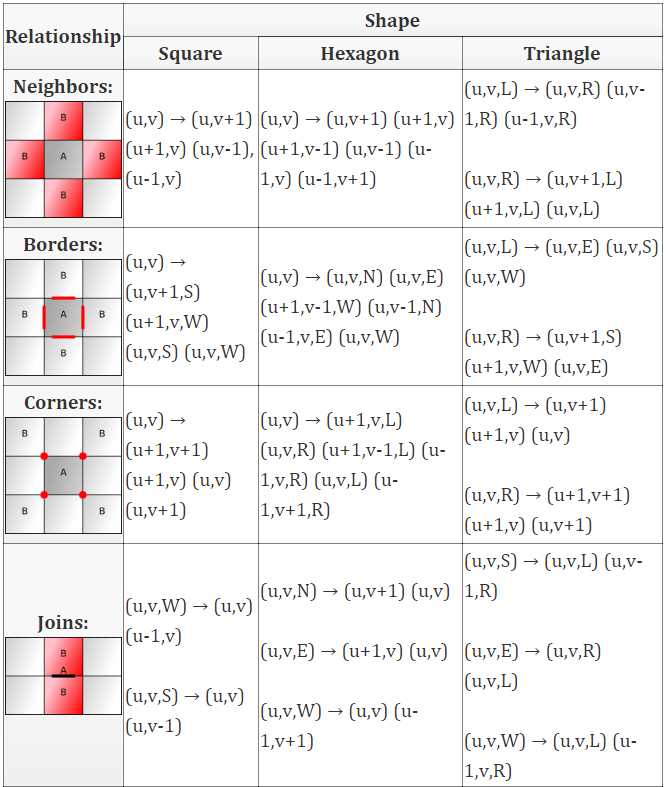
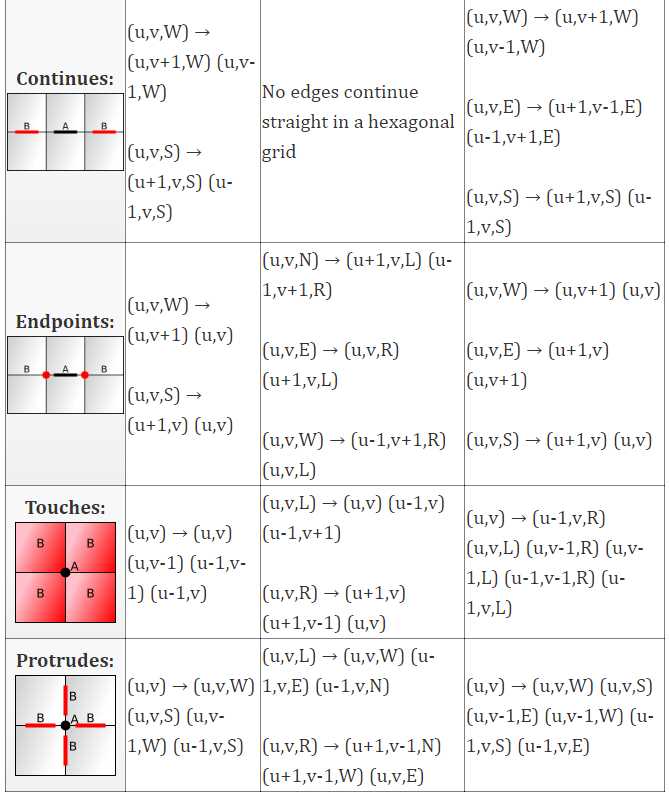
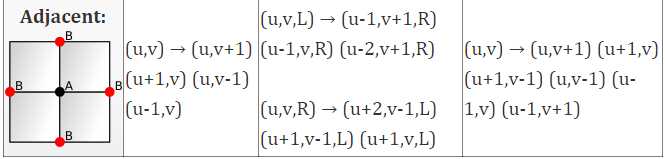
关系

（心情不好可跳过本节）

上面列出的关系本身就是相互关联的。例如，borders 从面到边，它是 joins 的颠倒，从边到面。

如果某些边B 位于某个面A 的 borders 列表中，则 A 将位于边B 的 joins 列表中。这9种关系可以归结为6种数学关系。

 

如果您有数据库，则可以直接表达关系。例如，这是一个小的 1x2 方格网格中面和边之间的关系：

 

 

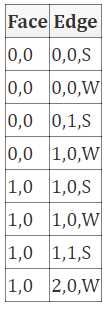
 给定关系，您可以在任何列中查找。

例如，使用上表，查找Face==(0,0)4个边的结果，这是 borders 关系表达的内容。

Edge==(1,0,W)在2个面中查找结果，这是 joints 关系表达的内容。

关系允许您以多种方式查找事物；每个关系（和算法）都是一种特定的查找方式。

 

给定 6 种关系，那么应该有 12 种关系。

为什么我们只有9个？

这是因为面/面，边/边和顶点/顶点关系是对称的，所以以另一种方式查找事物会产生相同的答案。

因此，12个关系中的3个是多余的，我们剩下9个。

实现

所有算法都很简单。你怎么能实现它们？

您首先要为三个坐标系中的每一个选择数据结构。

我建议保持它非常简单和透明。

我列出的所有坐标系都有一个整数u和一个整数v，其中一些有一个像L或的注释W。

对于结构，在Ruby中使用带有公共attrs的类；在Lisp中使用一个列表; 在C中使用结构；在Java中使用具有公共字段的类；在Python中使用简单的对象或字典。

对于注释，在Ruby或Lisp中，使用符号（‘L或:L）; 在C中，使用字符（‘L‘）或枚举类型（L）; 在Java中，使用字符; 在Python中，使用单字符字符串。

 

下一步是实现您需要的算法。

最简单的方法是编写带A的参数的函数（或方法）并返回B列表。

如果有多个A变体，请使用 switch / case 语句对注释进行分支。这是最简单的方法，但它并不是最快的。

为了加快速度，调用者可能会预先分配列表，或者您可能提供内联的回调（例如，C ++中的STL函数对象）。

在某些情况下，您需要同时查找多个A，因此您可以提供一个适用于A列表的算法，并生成B列表的列表。

 

我通常避免给出实现，因为它们对于每个游戏都太具体了，但我将举例说明 Ruby 中的 Triangle 形状。我选择使用列表作为我的基本数据结构，并使用 Ruby 符号（如:L）进行注释。

 

就这么简单。每个变体都成为case声明中的一种情况。

坐标转换

在2D和3D图形系统中，我们必须将“世界”坐标转换为“屏幕”坐标并返回。

对于网格，我们必须将“网格”坐标转换为“世界”坐标并返回。

转换将发生在点上。

从网格到世界坐标，我们变换顶点并以所在面的中心示之。

从世界到网格坐标，我们可以选择是找到包围点的面，或最接近点的边，还是最接近点的顶点。

正方形

这对正方形网格来说很容易。

如果正方形的边长为 s 且边与 x 和 y 轴对齐，则可以将网格顶点坐标乘以 s 得到世界坐标。

 

另一方面，我们想要确定哪个顶点最接近世界空间中的目标点。

我们可以将世界坐标除以 s 并将浮点数舍入为 int 以获得最近的顶点。

如果您想要确定哪个面包围世界空间中的一个点，请使用平面而不是圆形。

六边形

使用六边形比使用正方形稍微复杂一些。

 

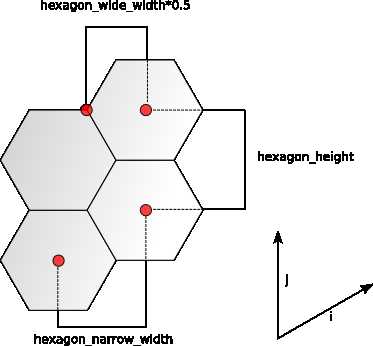
计算面的中心很简单。

有一个i向量和一个j向量。从六边形坐标到世界坐标是一个（非常简单的）矩阵乘法：

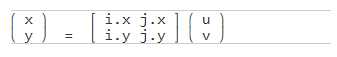
 展开来，即

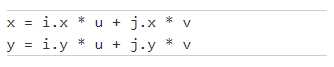
对于平顶六边形，i是(hexagon_narrow_width, 0.5*hexagon_height)和j是(0, hexagon_height)，所以给我们的值i.x, i.y, j.x, j.y。（尖顶六边形将与silghty不同）代码是：

计算顶点也很简单。

在文章的其余部分，我标记了六边形顶点 L 或 R。这两个顶点出现在六边形中心左侧或右侧的六边形宽度的一半，所以我们所要做的就是添加或减去 hexagon_wide_width * 0.5：

使用六边形时，将面中心视为主要，将顶点视为次要。

从六边形坐标(u, v)到世界坐标(x, y)是一个矩阵乘法。要从世界坐标返回到六边形，您可以求解方程式(u, v)。

我会跳过代数，这是平顶六边形的结果：

 

如果你从坐标为(x, y)的面中心开始，这是有效的。如果(x, y)是随机的点那就需要更多的操作了。

最简单（但不是最有效）的方法是考虑计算(u, v)加上所有邻居并确定哪一个最接近给定的世界坐标。此方法适用于所有三种网格类型。

如果您使用它来选择鼠标，这足够快。通过更仔细地观察多边形，可以进一步优化它。

三角形

三角形通过正方形被剪切和分裂得到。

三角形顶点仅使用剪切步骤，这会产生菱形。

要将三角形的顶点从网格坐标转换为世界坐标，请乘以轴向量 i 和j：

展开后，得到：

要将三角形面的坐标转换为世界坐标，需要进行调整。

对于面(u, v, L/R)首先计算左下顶点的世界坐标，(u, v)。

然后对于一个 L面，添加(1/2 * i, 1/3 * j)到左下顶点位置。

对于 R面，添加(i, 2/3 * j)到左下顶点位置。

结果将得到面部的中心。

 

要从世界坐标转换为三角形顶点，首先(u, v)使用代数找到菱形的左下角，或者通过反转 i.x，j.x，i.y，j.y 矩阵。

菱形包含两个三角形面。

要确定该点所在的面，请查看在每个菱形内划分两个三角形的边（边“E” ）。

如果 frac(u) + frac(v) < 1.0，该点在线的左侧，因此在 L面；否则就是在 R 面上。

 

使用三角形时，将顶点视为主要，将面中心视为次要。这与我们如何处理六边形相反。

更多

方形网格上的距离??公式是众所周知的（曼哈顿，欧几里德，对角线距离）。

使用此坐标系的十六进制网格上的距离??使用两轴坐标到第三轴的扩展，我在我的十六进制网格页面上有公式。我在这里探讨三角形网格上的距离。

 

有一些我找不到的地方放的东西，但你可能有兴趣。数学家在2D空间中发现了五种类型的网格：正方形，三角形，六边形，矩形和平行四边形。

但是，只有正方形，三角形和六边形是正多边形。

螺旋蜂窝马赛克是一种有趣的方法，可以在六边形网格中为六边形分配数字。它导致了一些奇怪的属性。