TELE poj1155 题解

Posted 2021-01-22 grharris

很明显，这道题是以1为根的树，存在最优子问题，因此考虑树形DP。

先看一下样例

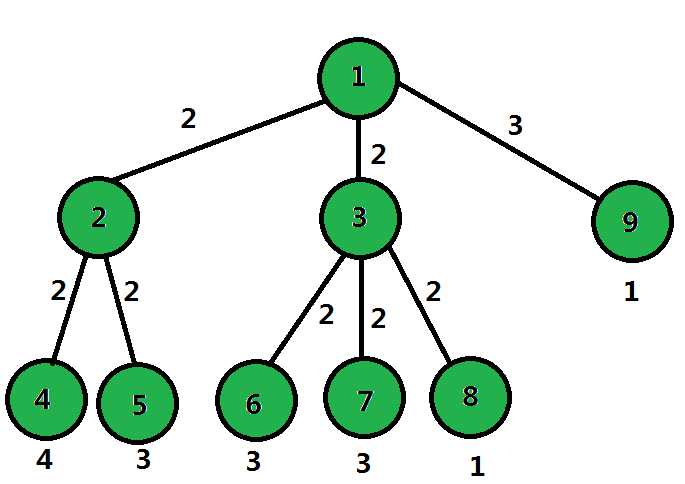树本来有向，请见谅

常识：利润=收入-成本，也就是：叶节点点权-边权

那么更加明显用dp[i][j]来记录在以i为根节点，使j个用户可以收视的最大利润。空间：3200*3200*4/1024/1024=39.0625MB，明显开的下

现在，推方程：每一次更新dp[i][j]，就相当于从i的该儿子中选取k个，再从除这个儿子以外的节点中选出j-k个，再减去将信号传给这个儿子的花费，就是从root到son边的权值

那么这样，很容易得出：为了计算dp[i][0],dp[i][1]...dp[i][size[i]],就枚举i的每一个儿子，然后，对于每一个儿子，枚举k，令dp[i][j]=max(dp[i][j-k]+dp[son][k]-pic[i][son])//为了方便，开了邻接矩阵

 1 for(int i=head[root];i!=-1;i=pic[i].nxt)//这里我用的链式前向星
 2 {
 3         int to=pic[i].to;
 4         for(int j=siz[root];j>=0;j--)
 5         {
 6             for(int k=min(siz[to],j);k>=0;k--)
 7             {
 8                 if(dp[root][j-k]!=-(1<<30))//dp初值设为负无穷，防止计算未算过的
 9                 {
10                     dp[root][j]=max(dp[root][j],dp[root][j-k]+dp[to][k]-pic[i].cot);
11                 }
12             }
13         }
14     }
15 }

现在，考虑枚举范围，如果每一次j，k都从n枚举到1，O(n³)，这道题也许能卡过。

优化：显而易见，j大于root的儿子的总数的部分，k大于to儿子总数的部分，都是无意义的，于是，每一次都更新size[root]，加上size[to]，再进行枚举，这样，由于每一个点都只与其他的点组合一次，就成功的优化到了O(n²)

在进行dp和dfs后，如何计算答案呢？

很简单，扫一遍dp[1][m],dp[1][m-1]...dp[1][0]直到找到第一个非负值，输出下标即可

送上AC代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m;
int p0,p1,p2;
struct edge
{
    int to,nxt,cot;
}pic[3200];
int head[3200];
int cnt=1;
int siz[3200];
int dp[3200][3200];
void add(int f,int t,int c)//链星
{
    pic[cnt].to=t;
    pic[cnt].nxt=head[f];
    pic[cnt].cot=c;
    head[f]=cnt;
    cnt++;
}
void dfs(int root)
{
    for(int i=head[root];i!=-1;i=pic[i].nxt) 
    {
        int to=pic[i].to;
        dfs(to);
        siz[root]+=siz[to];//更新siz
        for(int j=siz[root];j>=0;j--)//更新dp
        {
            for(int k=min(siz[to],j);k>=0;k--)
            {
                if(dp[root][j-k]!=-(1<<30))
                {
                    dp[root][j]=max(dp[root][j],dp[root][j-k]+dp[to][k]-pic[i].cot);
                }
            }
        }
    }
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n-m;i++)
    {
        scanf("%d",&p0);
        for(int j=1;j<=p0;j++)
        {
            scanf("%d%d",&p1,&p2);
            add(i,p1,p2);
        }
    }
    for(int i=1;i<=n;i++)//不要滥用memset
    {
        for(int j=1;j<=n;j++)//j不能从0枚举
        {
            dp[i][j]=-(1<<30);
        }
    }
    for(int i=n-m+1;i<=n;i++)
    {
        scanf("%d",&dp[i][1]);
        siz[i]=1;//siz存储叶子数目，因而其他的不用赋成1
    }
    dfs(1);
    for(int i=m;i>=0;i--)
    {
        if(dp[1][i]>=0)
        {
            printf("%d",i);
            return 0;
        }
    }
    printf("0");
    return 0;
}

实际上，本蒟蒻第一次交的时候TLE找不出原因，后来发现实际是调试时把dp改小而导致RE，所以再郑重提醒大家一次，一定要在交码前确认删净了调试代码，把数组改回来

蒟蒻写题解不易，如有问题敬请见谅