20172333 2018-2019-1 《程序设计与数据结构》第九周学习总结
Posted yanyujun527
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了20172333 2018-2019-1 《程序设计与数据结构》第九周学习总结相关的知识,希望对你有一定的参考价值。
20172333 2018-2019-1 《程序设计与数据结构》第九周学习总结
教材学习内容总结
《Java软件结构与数据结构》第十五章-图
一、无向图
- ①无向图的定义
- 图是由结点与结点相连接构成的,与树类似。这些结点被常常称作顶点(vertice),这些顶点的连接叫做边(edge)。
- 无向图(undirected graph)是一种边为无序结点对的图。
- 两个顶点之间有一条连通边的顶点,我们称作它们为领接的(adjacent)。这两个顶点也叫作邻居(neighbor),自己是自己的邻居叫做自循环(self-loop)。
- 一个完整的无向图就是拥有n(n-1)/2的边的无向图。(n是顶点数,且没有自循环)
- 长度是两个顶点的路径长度,即路径中的边的条数或者顶点数-1。
- 环路(cycle)是首顶点与尾顶点相同且没有重边的路径。
- 无向树是一种连通的无环无向图,其中一个元素被指定为树根。
图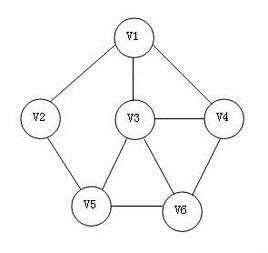
二、有向图
- ①有向图的定义
- 有向图是一种边为有序顶点对的图。
图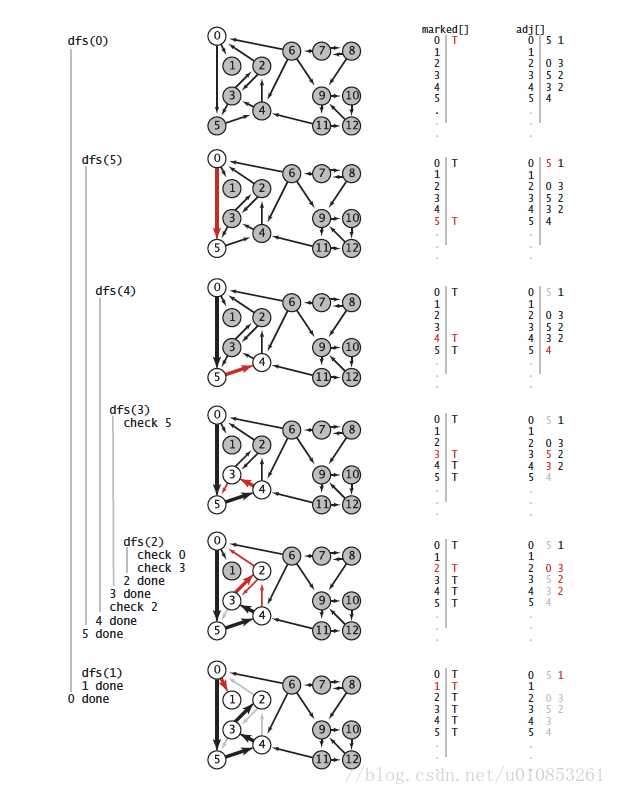
- 有向图是一种边为有序顶点对的图。
三、网络
- ①网络的定义
- 网络又被叫做加权图。
图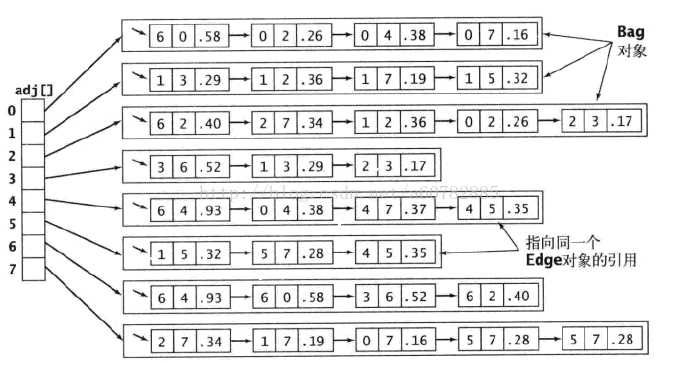
- 网络又被叫做加权图。
四、常用的图算法
- ①遍历
- 遍历被分为两种,一种叫广度优先遍历(Breadth-first travelsal),另外一种被叫做深度优先遍历(depth-first traversal)
- 这两个遍历的区别在于,深度优先遍历是使用栈来管理遍历,而广度优先遍历是使用队列。(书上粗略而又没有什么用的解释)
- 这两个遍历的使用效果区别:深度优先遍历是遇到分叉的顶点进行记录,并继续前进直到没有分叉后返回上一个分叉顶点。而广度优先遍历则是以扇形的模式对于周边的顶点遍历后再进行深入。
深度优先遍历示意图
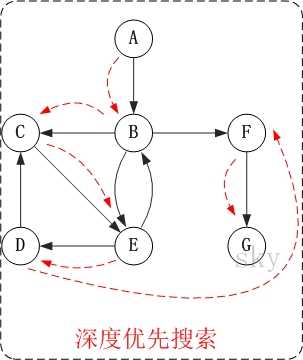
广度优先遍历示意图
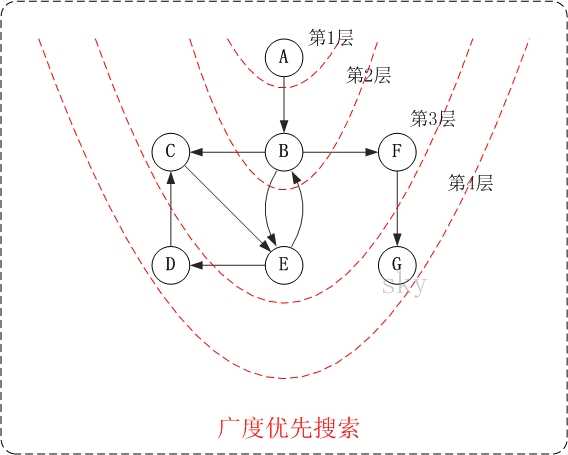
深度遍历与广度遍历代码
public Iterator<T> iteratorDFS(int startIndex)
{
Integer x;
boolean found;
StackADT<Integer> traversalStack = new LinkedStack<Integer>();
UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();
boolean[] visited = new boolean[numVertices];
if (!indexIsValid(startIndex))
return resultList.iterator();
for (int i = 0; i < numVertices; i++)
visited[i] = false;
traversalStack.push(new Integer(startIndex));
resultList.addToRear(vertices[startIndex]);
visited[startIndex] = true;
while (!traversalStack.isEmpty())
{
x = traversalStack.peek();
found = false;
//Find a vertex adjacent to x that has not been visited
// and push it on the stack
for (int i = 0; (i < numVertices) && !found; i++)
{
if (adjMatrix[x.intValue()][i] && !visited[i])
{
traversalStack.push(new Integer(i));
resultList.addToRear(vertices[i]);
visited[i] = true;
found = true;
}
}
if (!found && !traversalStack.isEmpty())
traversalStack.pop();
}
return new GraphIterator(resultList.iterator());
}
public Iterator<T> iteratorDFS(T startVertex)
{
return iteratorDFS(getIndex(startVertex));
}
public Iterator<T> iteratorBFS(int startIndex)
{
Integer x;
QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();
UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();
if (!indexIsValid(startIndex))
return resultList.iterator();
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false;
traversalQueue.enqueue(new Integer(startIndex));
visited[startIndex] = true;
while (!traversalQueue.isEmpty())
{
x = traversalQueue.dequeue();
resultList.addToRear(vertices[x.intValue()]);
//Find all vertices adjacent to x that have not been visited
// and queue them up
for (int i = 0; i < numVertices; i++)
{
if (adjMatrix[x.intValue()][i] && !visited[i])
{
traversalQueue.enqueue(new Integer(i));
visited[i] = true;
}
}
}
return new GraphIterator(resultList.iterator());
}
public Iterator<T> iteratorBFS(T startVertex)
{
return iteratorBFS(getIndex(startVertex));
}- ②测试连通性
- 只有在广度优先遍历中的顶点数与图中的顶点数相同的时候才是连通的。
- ③最小生成树
- 最小生成树就是该树的权重小于等于该图的其他生成树的权重。
- 最小生成树示意图(分两种算法,一种是Prim算法,适合边较稠密的那种,另外一种是Dijkstra算法,这种适用于顶点多的那种)图1
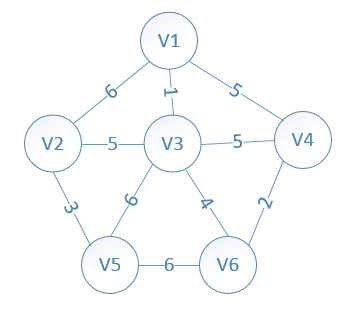
,图2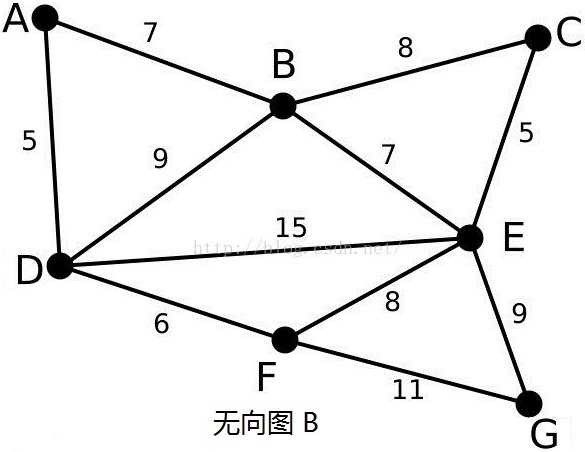
- 最小生成树推演算法
public Graph getMST()
{
int x, y;
int[] edge = new int[2];
StackADT<int[]> vertexStack = new LinkedStack<int[]>();
Graph<T> resultGraph = new Graph<T>();
if (isEmpty() || !isConnected())
return resultGraph;
resultGraph.adjMatrix = new boolean[numVertices][numVertices];
for (int i = 0; i < numVertices; i++)
for (int j = 0; j < numVertices; j++)
resultGraph.adjMatrix[i][j] = false;
resultGraph.vertices = (T[])(new Object[numVertices]);
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false;
edge[0] = 0;
resultGraph.vertices[0] = this.vertices[0];
resultGraph.numVertices++;
visited[0] = true;
// Add all edges that are adjacent to vertex 0 to the stack.
for (int i = 0; i < numVertices; i++)
{
if (!visited[i] && this.adjMatrix[0][i])
{
edge[1] = i;
vertexStack.push(edge.clone());
visited[i] = true;
}
}
while ((resultGraph.size() < this.size()) && !vertexStack.isEmpty())
{
// Pop an edge off the stack and add it to the resultGraph.
edge = vertexStack.pop();
x = edge[0];
y = edge[1];
resultGraph.vertices[y] = this.vertices[y];
resultGraph.numVertices++;
resultGraph.adjMatrix[x][y] = true;
resultGraph.adjMatrix[y][x] = true;
visited[y] = true;
for (int i = 0; i < numVertices; i++)
{
if (!visited[i] && this.adjMatrix[i][y])
{
edge[0] = y;
edge[1] = i;
vertexStack.push(edge.clone());
visited[i] = true;
}
}
}
return resultGraph;
}五、图的实现策略
- ①邻接列表与邻接矩阵
- 邻接列表的形式与之前我们学习处理哈希冲突所采用的数组与链表结合的方法类似,都是以数组的头结点来实现的列表。
邻接列表的示意图
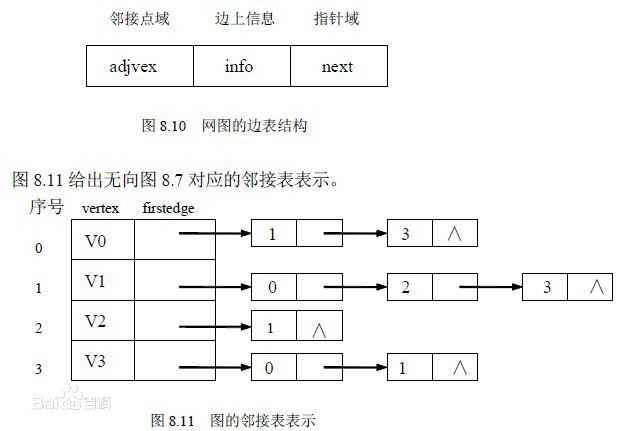
- 邻接矩阵分为两个部分,一个部分是一个一位数组用于存储每个顶点数据,另一个部分是一个二维数组用于存放每个顶点间的关系(边)的数据,这个二维数组就是邻接矩阵。
- 邻接矩阵的无向图有几个特点:
- 主对角线上必然为0
- 矩阵必然对称
矩阵的非0元素必然是边的2倍
用邻接矩阵实现无向图
- ①邻接矩阵扩展的GraphADT接口
public interface GraphADT<T>
{
/**
* Adds a vertex to this graph, associating object with vertex.
*
* @param vertex the vertex to be added to this graph
*/
public void addVertex(T vertex);
/**
* Removes a single vertex with the given value from this graph.
*
* @param vertex the vertex to be removed from this graph
*/
public void removeVertex(T vertex);
/**
* Inserts an edge between two vertices of this graph.
*
* @param vertex1 the first vertex
* @param vertex2 the second vertex
*/
public void addEdge(T vertex1, T vertex2);
/**
* Removes an edge between two vertices of this graph.
*
* @param vertex1 the first vertex
* @param vertex2 the second vertex
*/
public void removeEdge(T vertex1, T vertex2);
/**
* Returns a breadth first iterator starting with the given vertex.
*
* @param startVertex the starting vertex
* @return a breadth first iterator beginning at the given vertex
*/
public Iterator iteratorBFS(T startVertex);
/**
* Returns a depth first iterator starting with the given vertex.
*
* @param startVertex the starting vertex
* @return a depth first iterator starting at the given vertex
*/
public Iterator iteratorDFS(T startVertex);
/**
* Returns an iterator that contains the shortest path between
* the two vertices.
*
* @param startVertex the starting vertex
* @param targetVertex the ending vertex
* @return an iterator that contains the shortest path
* between the two vertices
*/
public Iterator iteratorShortestPath(T startVertex, T targetVertex);
/**
* Returns true if this graph is empty, false otherwise.
*
* @return true if this graph is empty
*/
public boolean isEmpty();
/**
* Returns true if this graph is connected, false otherwise.
*
* @return true if this graph is connected
*/
public boolean isConnected();
/**
* Returns the number of vertices in this graph.
*
* @return the integer number of vertices in this graph
*/
public int size();
/**
* Returns a string representation of the adjacency matrix.
*
* @return a string representation of the adjacency matrix
*/
public String toString();
}
- ②NetworkADT
public interface NetworkADT<T> extends GraphADT<T>
{
/**
* Inserts an edge between two vertices of this graph.
*
* @param vertex1 the first vertex
* @param vertex2 the second vertex
* @param weight the weight
*/
public void addEdge(T vertex1, T vertex2, double weight);
/**
* Returns the weight of the shortest path in this network.
*
* @param vertex1 the first vertex
* @param vertex2 the second vertex
* @return the weight of the shortest path in this network
*/
public double shortestPathWeight(T vertex1, T vertex2);
}
- ③addEdge方法实现
public void addEdge(T vertex1, T vertex2)
{
addEdge(getIndex(vertex1), getIndex(vertex2));
}
public void addEdge(int index1, int index2)
{
if (indexIsValid(index1) && indexIsValid(index2))
{
adjMatrix[index1][index2] = true;
adjMatrix[index2][index1] = true;
modCount++;
}
}- 在实现这个方法的时候调用了getIndex的方法来定位正确的索引。
教材学习中的问题和解决过程
- 问题1:图的概念与树的概念有重复的也有不同的地方,它们有什么区别?
- 回答1:树其实就是没有连接在一起的图,这里的没有连接在一起指的是连接成环。
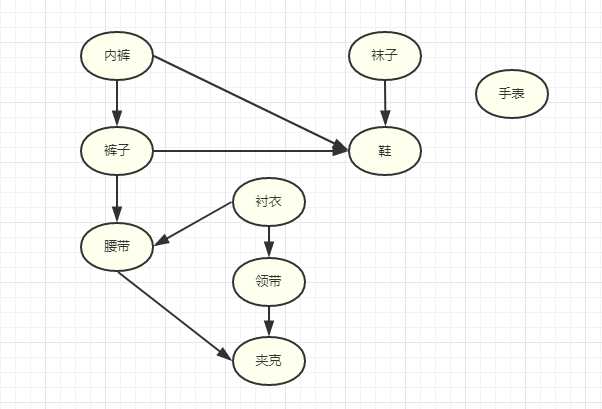
- 问题2:拓扑序是什么东西?
- 回答2:树上的解释是有向图中没有环路,且有一条从A到B的边,则可以把顶点A安排在顶点B之前。这种排序得到的顶点次序称为拓扑序。但是没图没真相,光从字面意思有点难以体会,然后我就去网上找到一个比较实际的拓扑序的图。后来我自己对于拓扑序的解释是“优先找到没有入边的点,将它打印出来,再将它的边和它本身删除,重复进行上次运算直到没有点。”
代码调试中的问题和解决过程
问题1:在做PP15.1的时候,进行测试连通方法的时候,我故意想要将所有顶点连接在一起,最后测试的时候,测试结果却是没有连通,图。
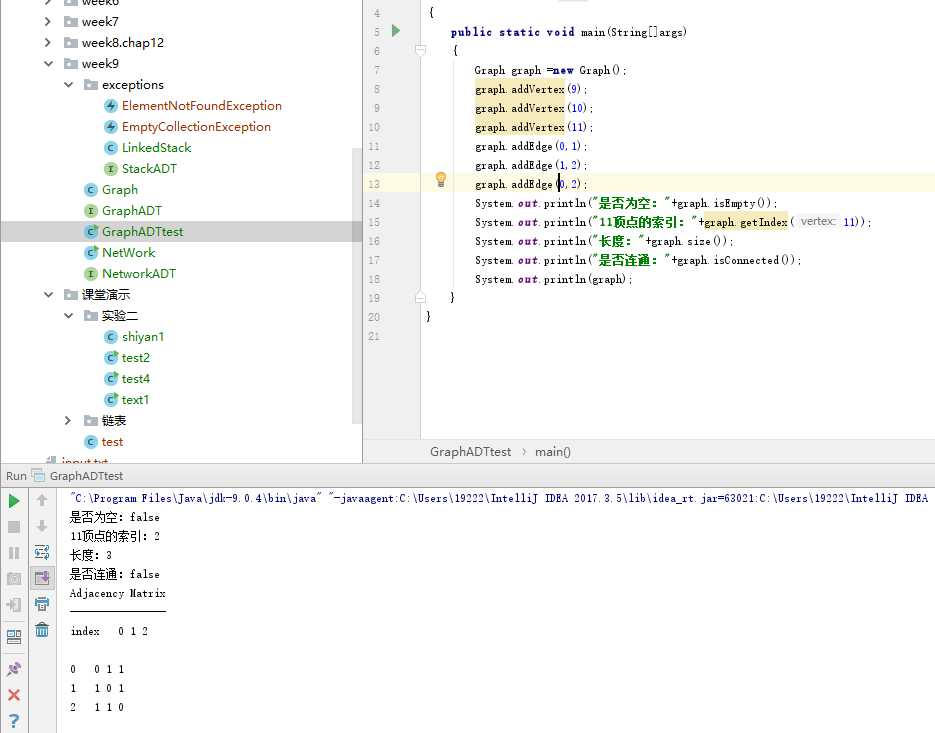
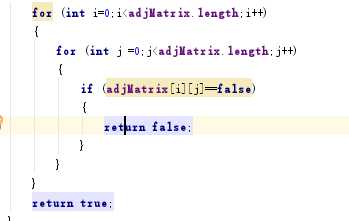
解决方案:在检查代码的过程中图,我发现了我的返回错误的要求不仅要建立A到B的边,也要建立B到A的边,否则就错误。
代码托管
-图代码
上周考试错题总结
- 无
结对及互评
基于评分标准,我给李楠的博客打分:7分。得分情况如下:
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, (加3分)
代码调试中的问题和解决过程, 无问题
感想,体会真切的(加1分)
点评认真,能指出博客和代码中的问题的(加1分)
点评过的同学博客和代码
- 本周结对学习情况
- 20172330李楠
- 结对照片
- 结对学习内容
- 图
其他(感悟、思考等,可选)
实现网络图的时候对于各种遍历运用极度不熟悉。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 10/10 | |
| 第二周 | 0/0 | 1/2 | 10/20 | |
| 第三周 | 1500/1500 | 1/3 | 10/30 | |
| 第四周 | 2761/4261 | 2/5 | 25/55 | |
| 第五周 | 814/5075 | 1/6 | 15/70 | |
| 第六周 | 1091/6166 | 1/7 | 15/85 | |
| 第七周 | 1118/7284 | 1/8 | 15/100 | |
| 第八周 | 1235/8519 | 2/10 | 15/115 | |
| 第九周 | 1757/10276 | 1/11 | 25/140 |
以上是关于20172333 2018-2019-1 《程序设计与数据结构》第九周学习总结的主要内容,如果未能解决你的问题,请参考以下文章
20172333 2018-2019-1 《程序设计与数据结构》第五周学习总结
# 20172333 2018-2019-1 《程序设计与数据结构》第八周学习总结
20172333 2018-2019-1 《程序设计与数据结构》第七周学习总结
20172333 2017-2018-2 《程序设计与数据结构》实验5报告