CVPR论文《100+ Times Faster Weighted Median Filter (WMF)》的实现和解析（附源代码）。
Posted imageshop
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了CVPR论文《100+ Times Faster Weighted Median Filter (WMF)》的实现和解析（附源代码）。相关的知识，希望对你有一定的参考价值。
四年前第一次看到《100+ Times FasterWeighted Median Filter (WMF)》一文时，因为他附带了源代码，而且还是CVPR论文，因此，当时也对代码进行了一定的整理和解读，但是当时觉得这个算法虽然对原始速度有不少的提高，但是还是比较慢。因此，没有怎么在意，这几天有几位朋友又提到这篇文章，于是把当时的代码和论文又仔细的研读了一番，对论文的思想和其中的实现也有了一些新的新的，再次做个总结和分享。
这篇文章的官网地址是：http://www.cse.cuhk.edu.hk/~leojia/projects/fastwmedian/，其中主要作者Jiaya Jia教授的官网地址是：http://jiaya.me/，根据Jiaya Jia的说法，这个算法很快将被OpenCv所收录，到时候OpenCv的大神应该对他还有所改进吧。
在百度上搜索加权中值模糊，似乎只有一篇博客对这个文章进行了简单的描述，详见：https://blog.csdn.net/streamchuanxi/article/details/79573302?utm_source=blogxgwz9。
由于作者只给出了最后的优化实现代码，而论文中还提出了各种中间过程的时间，因此本文以实现和验证论文中有关说法为主，涉及到的理论知识比较肤浅，一般是一笔而过。
根据论文中得说法，所谓的加权中值滤波，也是一种非线性的图像平滑技术，他取一个局部窗口内所有像素的加权中值来代替局部窗口的中心点的值。用较为数学的方法表示如下：
在图像I中的像素p，我们考虑以p为中心，半径为R的局部窗口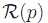
，不同于普通的中值模糊，对于属于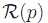内每一个像素q，都有一个基于对应的特征图像的相似度的权重系数wpq，如下式所示：
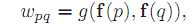
f(p)和f(q)是像素p和q在对应的特征图中得特征值。g是一个权重函数，最常用的即为高斯函数，反应了像素p和q的相似程度。
我们用I(q)表示像素点q的像素值，在窗口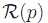内的像素总数量用n表示，则n=(2r+1)*(2r+1)，那么窗口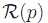内像素值和权重值构成一个对序列，即
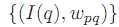，对这个序列按照I(q)的值进行排序。排序后，我们依次累加权重值，直到累加的权重大于等于所有权重值的一半时停止，此时对应的I(q)即作为本局部窗口中心点的新的像素值。
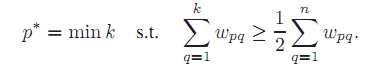
很明显，上面的过程要比标准的中值模糊复杂一些，在处理时多了特征图和权重函数项，而标准的中值模糊我们可以认为是加权中值模糊的特例，即所有局部窗口的权重都为1或者说相等。
在这里，特征图可以直接是源图像，也可以是其他的一些特征，比如原图像的边缘检测结果、局部均方差、局部熵或者其他的更为高级的特征。
按照这个定义，我们给出一段针对灰度数据的Brute-force处理代码：
int __cdecl ComparisonFunction(const void *X, const void *Y) // 一定要用__cdecl这个标识符
{
Value_Weight VWX = *(Value_Weight *)X;
Value_Weight VWY = *(Value_Weight *)Y;
if (VWX.Value < VWY.Value)
return -1;
else if (VWX.Value > VWY.Value)
return +1;
else
return 0;
}
// 加权中值模糊，直接按照算法的定义实现。
// Input - 输入图像，灰度图，LevelV = 256级
// FeatureMap - 特征图像，灰度图，LevelF = 256级
// Weight - 特征的权重矩阵，大小是LevelF * LevelF
// Output - 输出图像，不能和Input为同一个数据。
int IM_WeightedMedianBlur_00(unsigned char *Input, unsigned char *FeatureMap, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius)
{
int Channel = Stride / Width;
if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE;
if ((FeatureMap == NULL) || (Weight == NULL)) return IM_STATUS_NULLREFRENCE;
if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER;
if ((Channel != 1)) return IM_STATUS_NOTSUPPORTED;
const int LevelV = 256; // Value 可能出现的不同数量
const int LevelF = 256; // Feature 可能出现的不同数量
Value_Weight *VW = (Value_Weight *)malloc((2 * Radius + 1) * (2 * Radius + 1) * sizeof(Value_Weight)); // 值和特征序列对内存
if (VW == NULL) return IM_STATUS_OK;
for (int Y = 0; Y < Height; Y++)
{
unsigned char *LinePF = FeatureMap + Y * Stride;
unsigned char *LinePD = Output + Y * Stride;
for (int X = 0; X < Width; X++)
{
int CF_Index = LinePF[X] * LevelF;
int PixelAmount = 0;
float SumW = 0;
for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++)
{
int Index = J * Stride;
for (int I = IM_Max(X - Radius, 0); I <= IM_Min(X + Radius, Width - 1); I++) // 注意越界
{
int Value = Input[Index + I]; // 值
int Feature = FeatureMap[Index + I]; // 特征
float CurWeight = Weight[CF_Index + Feature]; // 对应的权重
VW[PixelAmount].Value = Value;
VW[PixelAmount].Weight = CurWeight; // 保存数据
SumW += CurWeight; // 计算累加数据
PixelAmount++; // 有效的数据量
}
}
float HalfSumW = SumW * 0.5f; // 一半的权重
SumW = 0;
qsort(VW, PixelAmount, sizeof VW[0], &ComparisonFunction); // 调用系统的qsort按照Value的值从小到大排序，注意qsort的结果仍然保存在第一个参数中
for (int I = 0; I < PixelAmount; I++) // 计算中值
{
SumW += VW[I].Weight;
if (SumW >= HalfSumW)
{
LinePD[X] = VW[I].Value;
break;
}
}
}
}
free(VW);
return IM_STATUS_OK;
}
很明显，这个函数的时间复杂度是o(radius * radius)，空间复杂度到时很小。
我们在一台 I5，3.3GHZ的机器上进行了测试，上述代码处理一副1000*1000像素的灰度图，半径为10（窗口大小21*21）时，处理时间约为27s，论文里给的Cpu和我的差不多，给出的处理one - metalpixel的RGB图用时90.7s，考虑到RGB的通道的数据量以及一些其他的处理，应该说论文如实汇报了测试数据。
那么从代码优化上面讲，上面代码虽然还有优化的地方，但是都是小打小闹了。使用VS的性能分析器，可以大概获得如下的结果：
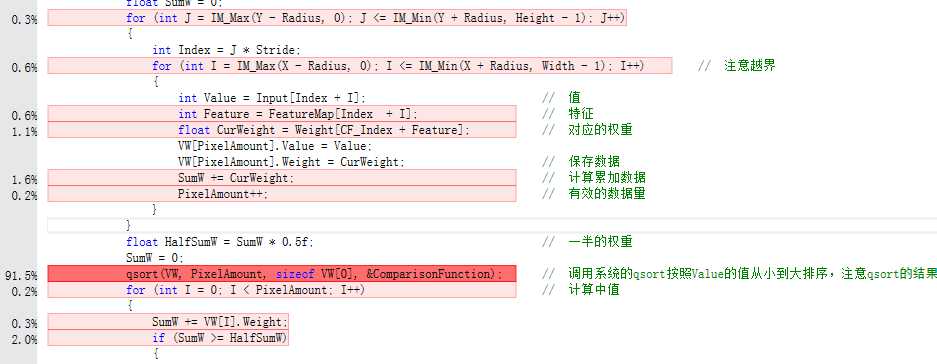
可见核心代码基本都用于排序了，使用更快的排序有助于进一步提高速度。
针对这个情况，论文的作者从多方面提出了改进措施，主要有三个方面，我们简单的重复下。
一、联合直方图(Joint Histgram）
直方图优化在很多算法中都有应用，比如标准的中值滤波，现在看到的最快的实现方式还是基于直方图的，详见：任意半径中值滤波（扩展至百分比滤波器）O(1)时间复杂度算法的原理、实现及效果，但是在加权中值滤波中，传统的一维直方图已经无法应用，因为这个算法不仅涉及到原图的像素值，还和另外一幅特征图有关，因此，文中提出了联合直方图，也是一种二维直方图。
如果图像中的像素最多有LevelV个不同值，其对应的特征最多有LevelF个不同的值，那么我们定义一个宽和高分别为LevelV * LevelF大小的直方图。对于某一个窗口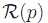，统计其内部的(2r+1)*(2r+1)个像素和特征对的直方图数据，即如果某个点的像素值为V，对应的特征值为F，则相应位置的直方图数据加1。
如果我们统计出这个二维的直方图数据后，由于中心点的特征值是固定的，因此，对于直方图的每一个LevelF值，权重是一定的了，我们只需计算出直方图内每一个Value值所对应所有的Feature的权重后，就可方便的统计出中值所在的位置了。
那么如果每个像素点都进行领域直方图的计算，这个的工作量也是蛮大的，同一维直方图的优化思路一样，在进行逐像素行处理的时候，对直方图数据可以进行逐步的更新，去除掉移走的那一列的直方图信息，在加入即将进入那一列数据，而中间重叠部分则不需要调整。
按照论文中的Joint Histgram的布局，即行方向大小为LevelV，列方向大小为LevelF，编制Joint Histgram实现的加权中值算法代码如下所示：
// 加权中值模糊，基于论文中图示的内存布局设置的Joint Histgram。
int IM_WeightedMedianBlur_01(unsigned char *Input, unsigned char *FeatureMap, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius)
{
int Channel = Stride / Width;
if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE;
if ((FeatureMap == NULL) || (Weight == NULL)) return IM_STATUS_NULLREFRENCE;
if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER;
if ((Channel != 1) && (Channel != 3)) return IM_STATUS_NOTSUPPORTED;
int Status = IM_STATUS_OK;
const int LevelV = 256; // Value 可能出现的不同数量
const int LevelF = 256; // Feature 可能出现的不同数量
int *Histgram = (int *)malloc(LevelF * LevelV * sizeof(int));
float *Sum = (float *)malloc(LevelV * sizeof(float));
if ((Histgram == NULL) || (Sum == NULL))
{
Status = IM_STATUS_OUTOFMEMORY;
goto FreeMemory;
}
for (int Y = 0; Y < Height; Y++)
{
unsigned char *LinePF = FeatureMap + Y * Stride;
unsigned char *LinePD = Output + Y * Stride;
memset(Histgram, 0, LevelF * LevelV * sizeof(int));
for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++)
{
for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++)
{
int Value = Input[J * Stride + I];
int Feature = FeatureMap[J * Stride + I]; // 统计二维直方图
Histgram[Feature * LevelV + Value]++;
}
}
for (int X = 0; X < Width; X++)
{
int Feature = LinePF[X];
float SumW = 0, HalfSumW = 0;;
for (int I = 0; I < LevelV; I++)
{
float Cum = 0;
for (int J = 0; J < LevelF; J++) // 计算每个Value列针对的不同的Feature的权重的累计值
{
Cum += Histgram[J * LevelV + I] * Weight[J * LevelF + Feature];
}
Sum[I] = Cum;
SumW += Cum;
}
HalfSumW = SumW / 2;
SumW = 0;
for (int I = 0; I < LevelV; I++)
{
SumW += Sum[I];
if (SumW >= HalfSumW) // 计算中值
{
LinePD[X] = I;
break;
}
}
if ((X - Radius) >= 0) // 移出的那一列的直方图
{
for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++)
{
int Value = Input[J * Stride + X - Radius];
int Feature = FeatureMap[J * Stride + X - Radius];
Histgram[Feature * LevelV + Value]--;
}
}
if ((X + Radius + 1) <= Width - 1) // 移入的那一列的直方图
{
for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++)
{
int Value = Input[J * Stride + X + Radius + 1];
int Feature = FeatureMap[J * Stride + X + Radius + 1];
Histgram[Feature * LevelV + Value]++;
}
}
}
}
FreeMemory:
if (Histgram != NULL) free(Histgram);
if (Sum != NULL) free(Sum);
return Status;
}
编译后测试，同样是21*21的窗口，one - metalpixel的灰度图像计算用时多达108s，比直接实现慢很多了。
分析原因，核心就是在中值的查找上，由于我们采用的内存布局方式，导致计算每个Value对应的权重累加存在的大量的Cache miss现象，即下面这条语句：
for (int J = 0; J < LevelF; J++) // 计算每个Value列针对的不同的Feature的权重的累计值 { Cum += Histgram[J * LevelV + I] * Weight[J * LevelF + Feature]; }
我们换种Joint Histgram的布局，即行方向大小为LevelF，列方向大小为LevelV，此时的代码如下：
// 加权中值模糊，修改内存布局设置的Joint Histgram。 int IM_WeightedMedianBlur_02(unsigned char *Input, unsigned char *FeatureMap, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius) { int Channel = Stride / Width; if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE; if ((FeatureMap == NULL) || (Weight == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3)) return IM_STATUS_NOTSUPPORTED; int Status = IM_STATUS_OK; const int LevelV = 256; // Value 可能出现的不同数量 const int LevelF = 256; // Feature 可能出现的不同数量 int *Histgram = (int *)malloc(LevelF * LevelV * sizeof(int)); float *Sum = (float *)malloc(LevelV * sizeof(float)); if ((Histgram == NULL) || (Sum == NULL)) { Status = IM_STATUS_OUTOFMEMORY; goto FreeMemory; } for (int Y = 0; Y < Height; Y++) { unsigned char *LinePF = FeatureMap + Y * Stride; unsigned char *LinePD = Output + Y * Stride; memset(Histgram, 0, LevelF * LevelV * sizeof(int)); for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Index = J * Stride; for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++) { int Value = Input[J * Stride + I]; int Feature = FeatureMap[J * Stride + I]; Histgram[Value * LevelF + Feature]++; // 注意索引的方式的不同 } } for (int X = 0; X < Width; X++) { int IndexF = LinePF[X] * LevelF; float SumW = 0, HalfSumW = 0;; for (int I = 0; I < LevelV; I++) { float Cum = 0; int Index = I * LevelF; for (int J = 0; J < LevelF; J++) // 核心就这里不同 { Cum += Histgram[Index + J] * Weight[IndexF + J]; } Sum[I] = Cum; SumW += Cum; } HalfSumW = SumW / 2; SumW = 0; for (int I = 0; I < LevelV; I++) { SumW += Sum[I]; if (SumW >= HalfSumW) { LinePD[X] = I; break; } } if ((X - Radius) >= 0) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X - Radius]; int Feature = FeatureMap[J * Stride + X - Radius]; Histgram[Value * LevelF + Feature]--; } } if ((X + Radius + 1) <= Width - 1) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X + Radius + 1]; int Feature = FeatureMap[J * Stride + X + Radius + 1]; Histgram[Value * LevelF + Feature]++; } } } } FreeMemory: if (Histgram != NULL) free(Histgram); if (Sum != NULL) free(Sum); return Status; }
修改后，同样的测试条件和图片，速度提升到了17s，仅仅是更改了一个内存布局而已，原论文的图没有采用这种布局方式，也许只是为了表达算法清晰而已。
和原论文比较，原论文的joint histgram时间要比直接实现慢（156.9s vs 90.7s)，而我这里的一个版本比brute force的快，一个比brute force的慢，因此，不清楚作者在比较时采用了何种编码方式，但是这都不重要，因为他们的区别都还在一个数量级上。
由于直方图大小是固定的，因此，前面的中值查找的时间复杂度是固定的，而后续的直方图更新则是o(r)的，但是注意到由于LevelV和 LevelF通常都是比较大的常数（一般为256），因此实际上，中值查找这一块的耗时占了绝对的比例。
二、快速中值追踪
寻找中值的过程实际上可以看成一个追求平衡的过程，假定当前搜索到的位置是V，位于V左侧所有相关值的和是Wl，位于V右侧所有相关值得和是Wr，则中值的寻找可以认为是下式：
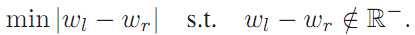
后面的约束条件可以理解为第一次出现Wl大于Wr前。
如果我们之前已经寻找到了像素P处的中值，那么由于像素的连续性，像素P+1处的中值一般不会和P处的中值差异太大，大量的统计数据表明他们的差异基本在8个像素值之类（256色阶图），那么这个思想其实和任意半径中值滤波（扩展至百分比滤波器）O(1)时间复杂度算法的原理、实现及效果中讲到的是一致的。这种特性，我们也可以将他运用到加权中值滤波中。
考虑到加权中值滤波中联合直方图的特殊性，我们需要维护一张平衡表，论文中叫做Balance Counting Box(BCB)，这一块的解释比较拗口也比较晦涩，大家需要仔细的看论文和我下面提供的JointHist+MedianTracking代码。
// 加权中值模糊, Joint + MT int IM_WeightedMedianBlur_03(unsigned char *Input, unsigned char *FeatureMap, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius) { int Channel = Stride / Width; if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE; if ((FeatureMap == NULL) || (Weight == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3)) return IM_STATUS_NOTSUPPORTED; int Status = IM_STATUS_OK; const int LevelV = 256; // Value 可能出现的不同数量 const int LevelF = 256; // Feature 可能出现的不同数量 int *Histgram = (int *)malloc(LevelF * LevelV * sizeof(int)); int *BCB = (int *)malloc(LevelF * sizeof(int)); if ((Histgram == NULL) || (BCB == NULL)) { Status = IM_STATUS_OK; return IM_STATUS_OUTOFMEMORY; } for (int Y = 0; Y < Height; Y++) { unsigned char *LinePF = FeatureMap + Y * Stride; unsigned char *LinePD = Output + Y * Stride; memset(Histgram, 0, LevelF * LevelV * sizeof(int)); // 全部赋值为0 memset(BCB, 0, LevelF * sizeof(int)); int CutPoint = -1; for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Index = J * Stride; for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++) { int Value = Input[J * Stride + I]; int Feature = FeatureMap[J * Stride + I]; Histgram[Value * LevelF + Feature]++; // 计算每行第一个点的二维直方图，直方图的水平方向为Feature坐标，垂直方向为Value坐标 BCB[Feature]--; // 此时的CutPoint初始化为-1，所以+方向的数据为0，所有的都在-方向 } } for (int X = 0; X < Width; X++) { float BalanceWeight = 0; int IndexF = LinePF[X] * LevelF; // 中心点P的Value所对应的那一行Feature权重起始索引 for (int I = 0; I < LevelF; I++) // BCB[I]中保存的是以CutPoint为分界线，Feature为I时，分界线左侧的所有Value[0-CutPoint]值的数量和分界线右侧所有的Value（CutPoint， LevelV - 1]值数量的差异 { BalanceWeight += BCB[I] * Weight[IndexF + I]; // 因为Feature为固定值时，如果中心点固定，那么不管与Feature对应的Value值时多少，Weight就是定值了。 } if (BalanceWeight < 0) // 第一个点的BalanceWeight必然小于0 { for (; BalanceWeight < 0 && CutPoint != LevelV - 1; CutPoint++) { int IndexH = (CutPoint + 1) * LevelF; // 新的直方图的位置 float CurWeight = 0; for (int I = 0; I < LevelF; I++) { CurWeight += 2 * Histgram[IndexH + I] * Weight[IndexF + I]; // 左侧加右侧同时减，所以是2倍 BCB[I] += Histgram[IndexH + I] * 2; // 数量是同样的道理 } BalanceWeight += CurWeight; } } else if (BalanceWeight > 0) // 如果平衡值大于0，则向左移动中间值 { for (; BalanceWeight > 0 && CutPoint != 0; CutPoint--) { int IndexH = CutPoint * LevelF; float CurWeight = 0; for (int I = 0; I < LevelF; I++) { CurWeight += 2 * Histgram[IndexH + I] * Weight[IndexF + I]; BCB[I] -= Histgram[IndexH + I] * 2; } BalanceWeight -= CurWeight; } } LinePD[X] = CutPoint; if ((X - Radius) >= 0) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) // 即将移出的那一列数据 { int Value = Input[J * Stride + X - Radius]; int Feature = FeatureMap[J * Stride + X - Radius]; Histgram[Value * LevelF + Feature]--; if (Value <= CutPoint) // 如果移出的那个值小于当前的中值 BCB[Feature]--; else BCB[Feature]++; } } if ((X + Radius + 1) <= Width - 1) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X + Radius + 1]; int Feature = FeatureMap[J * Stride + X + Radius + 1]; Histgram[Value * LevelF + Feature]++; if (Value <= CutPoint) // 如果移出的那个值小于当前的中值 BCB[Feature]++; else BCB[Feature]--; } } } } free(Histgram); free(BCB); }
代码也很简洁，主要是增加了一个BCB列表的维护，编译后测试，同样是21*21的窗口，one - metalpixel的灰度图像计算用420ms左右，比Brute-force版本的27s大约快了64倍，这个和论文的时间比例基本差不多(（156.9+0.4）/(2.2+0.5)=58)。提速也是相当的可观，而且算法速度和半径不是特别敏感，毕竟更新直方图的计算量在这里占的比例其实已经不多了。
三、Necklace Table
那么论文最后还提出了另外的进一步加速的方案，这是基于以下观察到的事实，即在直方图的数据中，存在大量的0值，这些值的计算其实对算法本身是没有任何作用的，但是占用了大量的计算时间。
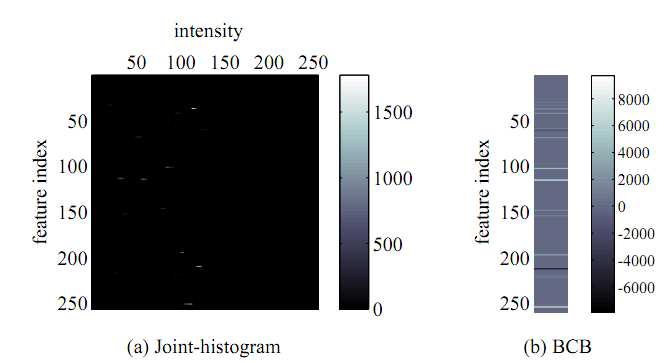
比如上图是某个图像局部窗口的联合直方图和BCB值，在联合直方图中大部分区域都是0值对应的黑色，在BCB中大部分情况也是0值。
因此，作者构建了一个叫做Necklace Table的数据结构，这个数据结构可以方便快捷的记录下一个和上一个非0元素的位置，从而能有效的访问到那些真正有计算价值的部位，以及简单的删除和增加节点的功能，具体的实现细节详见论文或下面的JointHistgram + Necklace Table代码。
int IM_WeightedMedianBlur_04(unsigned char *Input, unsigned char *FeatureMap, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius) { int Channel = Stride / Width; if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE; if ((FeatureMap == NULL) || (Weight == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3)) return IM_STATUS_NOTSUPPORTED; int Status = IM_STATUS_OK; const int LevelV = 256; // Value 可能出现的不同数量 const int LevelF = 256; // Feature 可能出现的不同数量 const int LevelV = 256; int *Histgram = (int *)malloc(LevelF * LevelV * sizeof(int)); int *ForwardH = (int *)malloc(LevelF * LevelV * sizeof(int)); // forward link for necklace table int *BackWordH = (int *)malloc(LevelF * LevelV * sizeof(int)); // forward link for necklace table float *Sum = (float *)malloc(LevelV * sizeof(float)); if ((Histgram == NULL) || (ForwardH == NULL) || (BackWordH == NULL) || (Sum == NULL)) { Status = IM_STATUS_OK; goto FreeMemory; } memset(ForwardH, 0, LevelF * LevelV * sizeof(int)); memset(BackWordH, 0, LevelF * LevelV * sizeof(int)); for (int Y = 0; Y < Height; Y++) { unsigned char *LinePF = FeatureMap + Y * Stride; unsigned char *LinePD = Output + Y * Stride; memset(Histgram, 0, LevelF * LevelV * sizeof(int)); for (int X = 0; X < LevelV; X++) { ForwardH[X * LevelF] = 0; // 其实每一个Feature对应一个完整的Necklace Table，需要把第一个元素置为0 BackWordH[X * LevelF] = 0; } for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) // 第一个元素 { int Index = J * Stride; for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++) { int Value = Input[Index + I]; int Feature = FeatureMap[Index + I]; int Index = Value * LevelF; if (Histgram[Index + Feature] == 0 && Feature != 0) // 直方图数据如果还是0并且FMap值不为0 { int T = ForwardH[Index]; ForwardH[Index] = Feature; ForwardH[Index + Feature] = T; BackWordH[Index + T] = Feature; BackWordH[Index + Feature] = 0; } Histgram[Index + Feature]++; } } for (int X = 0; X < Width; X++) { int IndexF = LinePF[X] * LevelF; float SumW = 0, HalfSumW = 0;; for (int I = 0; I < LevelV; I++) { float Cum = 0; int Index = I * LevelF; int J = 0; do { Cum += Histgram[Index + J] * Weight[IndexF + J]; // 跳过那些非0的元素 J = ForwardH[Index + J]; } while (J != 0); Sum[I] = Cum; // 计算每一个Value对应的所有Featrue的权重累计和 SumW += Cum; } HalfSumW = SumW / 2; SumW = 0; for (int I = 0; I < LevelV; I++) { SumW += Sum[I]; if (SumW >= HalfSumW) { LinePD[X] = I; break; } } if ((X - Radius) >= 0) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X - Radius]; int Feature = FeatureMap[J * Stride + X - Radius]; int Index = Value * LevelF; Histgram[Index + Feature]--; if (Histgram[Index + Feature] == 0 && Feature != 0) { int T1 = BackWordH[Index + Feature]; int T2 = ForwardH[Index + Feature]; ForwardH[Index + T1] = T2; BackWordH[Index + T2] = T1; } } } if ((X + Radius + 1) <= Width - 1) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X + Radius + 1]; int Feature = FeatureMap[J * Stride + X + Radius + 1]; int Index = Value * LevelF; if (Histgram[Index + Feature] == 0 && Feature != 0) // 直方图数据如果还是0并且FMap值不为0 { int T = ForwardH[Index]; ForwardH[Index] = Feature; ForwardH[Index + Feature] = T; BackWordH[Index + T] = Feature; BackWordH[Index + Feature] = 0; } Histgram[Index + Feature]++; } } } } FreeMemory: if (Histgram != NULL) free(Histgram); if (ForwardH != NULL) free(ForwardH); if (BackWordH != NULL) free(BackWordH); if (Sum != NULL) free(Sum); return Status; }
代码量不大，编译后测试，同样是21*21的窗口，one - metalpixel的灰度图像计算用1200ms左右，比Brute-force版本的27s大约快了22倍，由于这个算法和图像内容是由一定关系的，因此，和论文提供的数据直接比较的意义不大。
四、最终的结合体
很自然的，我们想到要把Median Tracking 和 Necklace Table联合在一起，来进一步的提高速度，这个时候可以对Joint Histgram即BCB都使用 Necklace Table来记录非零元素，于是产生了以下的结合代码：
int IM_WeightedMedianBlur_05(unsigned char *Input, unsigned char *FeatureMap, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius) { int Channel = Stride / Width; if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE; if ((FeatureMap == NULL) || (Weight == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3) && (Channel != 4)) return IM_STATUS_NOTSUPPORTED; int Status = IM_STATUS_OK; const int LevelV = 256; const int LevelF = 256; int *Histgram = (int *)malloc(LevelF * LevelV * sizeof(int)); int *BCB = (int *)malloc(LevelF * sizeof(int)); int *ForwardH = (int *)malloc(LevelF * LevelV * sizeof(int)); // forward link for necklace table int *BackWordH = (int *)malloc(LevelF * LevelV * sizeof(int)); // forward link for necklace table int *ForwardBCB = (int *)malloc(LevelF * sizeof(int)); // forward link for necklace table int *BackWordBCB = (int *)malloc(LevelF * sizeof(int)); // forward link for necklace table if ((Histgram == NULL) || (BCB == NULL) || (ForwardH == NULL) || (BackWordH == NULL) || (ForwardBCB == NULL) || (BackWordBCB == NULL)) { Status = IM_STATUS_OK; goto FreeMemory; } memset(ForwardH, 0, LevelF * LevelV * sizeof(int)); memset(BackWordH, 0, LevelF * LevelV * sizeof(int)); memset(ForwardBCB, 0, LevelF * sizeof(int)); memset(BackWordBCB, 0, LevelF * sizeof(int)); for (int Y = 0; Y < Height; Y++) { unsigned char *LinePF = FeatureMap + Y * Stride; unsigned char *LinePD = Output + Y * Stride; memset(Histgram, 0, LevelF * LevelV * sizeof(int)); // 全部赋值为0 memset(BCB, 0, LevelF * sizeof(int)); for (int X = 0; X < LevelV; X++) { ForwardH[X * LevelF] = 0; BackWordH[X * LevelF] = 0; } ForwardBCB[0] = 0; BackWordBCB[0] = 0; int CutPoint = -1; for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Index = J * Stride; for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++) { int Value = Input[Index + I]; int Feature = FeatureMap[Index + I]; int Index = Value * LevelF; if (Histgram[Index + Feature] == 0 && Feature != 0) // 直方图数据如果还是0并且FMap值不为0 { int T = ForwardH[Index]; ForwardH[Index] = Feature; ForwardH[Index + Feature] = T; BackWordH[Index + T] = Feature; BackWordH[Index + Feature] = 0; } Histgram[Index + Feature]++; // 计算每行第一个点的二维直方图，直方图的水平方向为Feature坐标，垂直方向为Value坐标 UpdateBCB(BCB[Feature], ForwardBCB, BackWordBCB, Feature, -1); // 此时的CutPoint初始化为-1，所以+方向的数据为0，所有的都在-方向 } } for (int X = 0; X < Width; X++) { float BalanceWeight = 0; int IndexF = LinePF[X] * LevelF; // 中心点P的Value所对应的那一行Feature权重起始索引 int I = 0; do { BalanceWeight += BCB[I] * Weight[IndexF + I]; // 按照当前BCB数据计算平衡值，BCB记录了相同的FMap值时按照之前的中间值左右两侧像素个数的差异值 I = ForwardBCB[I]; } while (I != 0); if (BalanceWeight < 0) // 第一个点的BalanceWeight必然小于0 { for (; BalanceWeight < 0 && CutPoint != LevelV - 1; CutPoint++) { int IndexH = (CutPoint + 1) * LevelF; // 新的直方图的位置 float CurWeight = 0; int I = 0; do { CurWeight += 2 * Histgram[IndexH + I] * Weight[IndexF + I]; // 左侧加右侧同时减，所以是2倍 UpdateBCB(BCB[I], ForwardBCB, BackWordBCB, I, Histgram[IndexH + I] << 1); I = ForwardH[IndexH + I]; } while (I != 0); BalanceWeight += CurWeight; } } else if (BalanceWeight > 0) // 如果平衡值大于0，则向左移动中间值 { for (; BalanceWeight > 0 && CutPoint != 0; CutPoint--) { int IndexH = CutPoint * LevelF; float CurWeight = 0; int I = 0; do { CurWeight += 2 * Histgram[IndexH + I] * Weight[IndexF + I]; // 左侧加右侧同时减，所以是2倍 UpdateBCB(BCB[I], ForwardBCB, BackWordBCB, I, -(Histgram[IndexH + I] << 1)); I = ForwardH[IndexH + I]; } while (I != 0); BalanceWeight -= CurWeight; } } LinePD[X] = CutPoint; if ((X - Radius) >= 0) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) // 即将移出的那一列数据 { int Value = Input[J * Stride + X - Radius]; int Feature = FeatureMap[J * Stride + X - Radius]; int Index = Value * LevelF; Histgram[Index + Feature]--; if (Histgram[Index + Feature] == 0 && Feature != 0) { int T1 = BackWordH[Index + Feature]; int T2 = ForwardH[Index + Feature]; ForwardH[Index + T1] = T2; BackWordH[Index + T2] = T1; } UpdateBCB(BCB[Feature], ForwardBCB, BackWordBCB, Feature, -((Value <= CutPoint) << 1) + 1); } } if ((X + Radius + 1) <= Width - 1) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X + Radius + 1]; int Feature = FeatureMap[J * Stride + X + Radius + 1]; int Index = Value * LevelF; if (Histgram[Index + Feature] == 0 && Feature != 0) // 直方图数据如果还是0并且FMap值不为0 { int T = ForwardH[Index]; ForwardH[Index] = Feature; ForwardH[Index + Feature] = T; BackWordH[Index + T] = Feature; BackWordH[Index + Feature] = 0; } UpdateBCB(BCB[Feature], ForwardBCB, BackWordBCB, Feature, ((Value <= CutPoint) << 1) - 1); Histgram[Index + Feature]++; } } } } FreeMemory: if (Histgram != NULL) free(Histgram); if (BCB != NULL) free(BCB); if (ForwardH != NULL) free(ForwardH); if (BackWordH != NULL) free(BackWordH); if (ForwardBCB != NULL) free(ForwardBCB); if (BackWordBCB != NULL) free(BackWordBCB); return Status; }
我们满怀期待的编译和执行他，结果出来了，同样是21*21的窗口，one - metalpixel的灰度图像计算用430ms左右，和Joint + MT的速度差不多，但是论文里给出的数据是Joint + MT + NT要比Joint + MT快3倍左右。这是怎么回事呢。
我们仔细检查论文里，在Implementation Notes节里有这样的语句：
Only a single thread is used without involving any SIMD instructions. Our system is implemented using C++.
第一，他也是用的C++和我一样，第二，他是单线程，也和我一样，第三，没有使用任何SIMD指令，似乎我也没有使用啊，都一样，为什么结果比对不一致，难道是大神他们作弊，鉴于他们的成就，我立即撤回我这逆天的想法，一定是其他地方有问题。我们试着反编译看看。
我们定位到Joint + MT的算法的下面一句代码看看：
for (int I = 0; I < LevelF; I++) // BCB[I]中保存的是以CutPoint为分界线，Feature为I时，分界线左侧的所有Value[0-CutPoint]值的数量和分界线右侧所有的Value（CutPoint， LevelV - 1]值数量的差异 { BalanceWeight += BCB[I] * Weight[IndexF + I]; // 因为Feature为固定值时，如果中心点固定，那么不管与Feature对应的Value值时多少，Weight就是定值了。 }
反编译结果为：
for (int I = 0; I < LevelF; I++) // BCB[I]中保存的是以CutPoint为分界线，Feature为I时，分界线左侧的所有Value[0-CutPoint]值的数量和分界线右侧所有的Value（CutPoint， LevelV - 1]值数量的差异 { BalanceWeight += BCB[I] * Weight[IndexF + I]; // 因为Feature为固定值时，如果中心点固定，那么不管与Feature对应的Value值时多少，Weight就是定值了。 0FAF1B25 movdqu xmm0,xmmword ptr [ecx] 0FAF1B29 add ecx,10h 0FAF1B2C cvtdq2ps xmm1,xmm0 0FAF1B2F movups xmm0,xmmword ptr [eax] 0FAF1B32 add eax,10h 0FAF1B35 mulps xmm1,xmm0 0FAF1B38 addps xmm2,xmm1 0FAF1B3B dec edx 0FAF1B3C jne IM_WeightedMedianBlur_03+1B5h (0FAF1B25h) }
赤裸裸的SIMD指令啊。
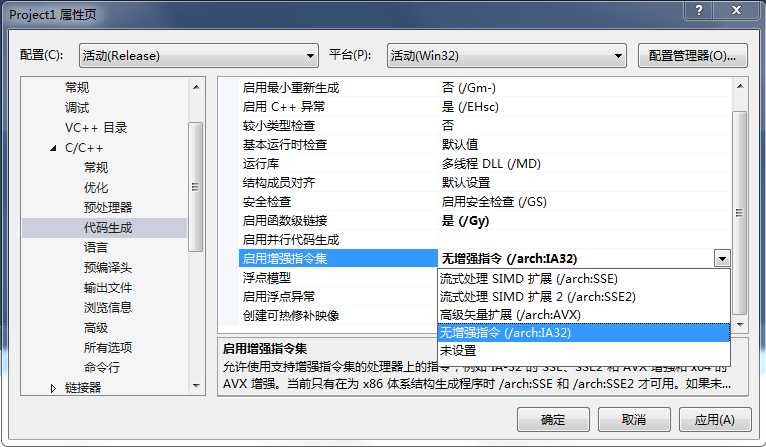
为什么呢，只是因为VS的编译器即使在默认情况下的设置中，也会根据当前编译系统的情况，进行一定的向量化优化，加上现在的PC基本没有哪一个不能使用SIMD指令的。如下图所示，为C++默认编译选项：
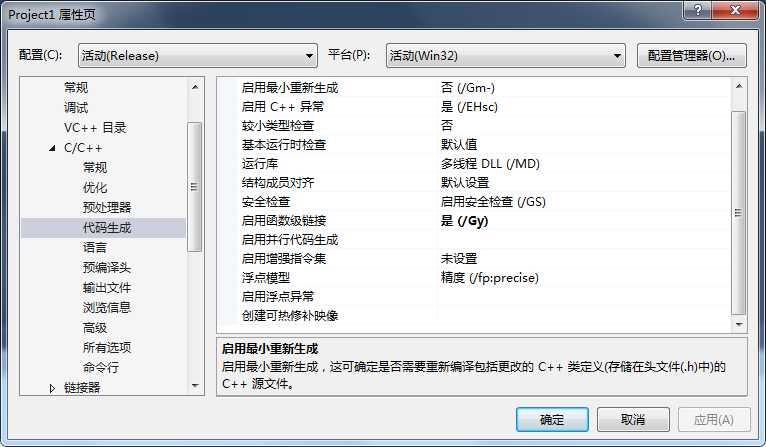
在启用增强指令集选项里默认是未设置，但是未设置并不代表不使用，正如上述所言，测试编译器会根据系统状况优化编译。因此，虽然表面上代码没有使用SIMD指令，但是实际却使用了。
为了公平起见，我们禁用系统的SIMD优化，此时，可以在增强指令集的选项里选择“无增强指令/arch:IA32".
编译后，对上述同样一段代码进行反编译，可以看到如下汇编码：
for (int I = 0; I < LevelF; I++) // BCB[I]中保存的是以CutPoint为分界线，Feature为I时，分界线左侧的所有Value[0-CutPoint]值的数量和分界线右侧所有的Value（CutPoint， LevelV - 1]值数量的差异 { BalanceWeight += BCB[I] * Weight[IndexF + I]; // 因为Feature为固定值时，如果中心点固定，那么不管与Feature对应的Value值时多少，Weight就是定值了。 0F8F1AF5 fild dword ptr [ecx-4] 0F8F1AF8 fmul dword ptr [eax+4] 0F8F1AFB fild dword ptr [ecx-8] 0F8F1AFE fmul dword ptr [eax] 0F8F1B00 faddp st(2),st 0F8F1B02 faddp st(1),st 0F8F1B04 fild dword ptr [ecx] 0F8F1B06 fmul dword ptr [eax+8] 0F8F1B09 faddp st(1),st 0F8F1B0B fild dword ptr [ecx+4] 0F8F1B0E fmul dword ptr [eax+0Ch] 0F8F1B11 faddp st(1),st 0F8F1B13 fild dword ptr [ecx+8] 0F8F1B16 fmul dword ptr [eax+10h] 0F8F1B19 faddp st(1),st 0F8F1B1B fild dword ptr [ecx+0Ch] 0F8F1B1E fmul dword ptr [eax+14h] 0F8F1B21 faddp st(1),st 0F8F1B23 fild dword ptr [ecx+10h] 0F8F1B26 fmul dword ptr [eax+18h] 0F8F1B29 faddp st(1),st 0F8F1B2B fild dword ptr [ecx+14h] 0F8F1B2E add ecx,20h 0F8F1B31 fmul dword ptr [eax+1Ch] 0F8F1B34 add eax,20h 0F8F1B37 faddp st(1),st 0F8F1B39 dec edi 0F8F1B3A jne IM_WeightedMedianBlur_03+1B5h (0F8F1AF5h) }
这里是明显的普通的FPU代码，多说一句，针对这个循环，系统也进行了多路并行优化。
为了比较方便，我们把禁用系统优化后的时间和未禁用是做一个整体的对比：
|
算法名称 |
执行时间 |
|
|
禁用编译器优化 |
启用编译器优化 |
|
|
BruteForce |
26875ms |
27025ms |
|
Joint Histgram |
123432ms |
108254ms |
|
Joint Hist CacheFriend |
55214ms |
17325ms |
|
Joint + MT |
1075ms |
420ms |
|
Joint + NT |
1286ms |
1200ms |
|
Joint + MT + NT |
422ms |
430ms |
当禁用编译器优化后，可以明显的看到Joint + MT + NT的速度优势比较大，和论文里给出的数据也基本相当了。
但是我们还是稍作分析，为什么同样是开启编译器优化，Joint + MT的速度能从1075ms降低到420ms，而Joint + MT + NT确基本没有什么变化呢，这就要从代码本身说起。
我们注意到，在Joint + MT版本中，BalanceWeight和CurWeight等元素的计算都是通过一个简单的for循环进行的，计算过程中循环的次数是固定的，每次计算内部的循环变量取值也是按照内存顺序来的，这种代码非常适合编译器使用SIMD指令优化，他会自动编译一系列带P（Packet）字母的SIMD指令（例如mulps）进行单周期四指令的快速执行，相当于提高了4倍的通行能力，而那些计算在整个算法里占用的时间比例有比较大，这样对整个算法的提速表现贡献是很大的。
而在有了Necklace Table参与的版本中，由于BalanceWeight和CurWeight的更新使用do while循环，循环的次数是未知的，循环里的指针指向的位置也是变动的，因此，即使使用了SIMD指令，他也只能使用其中带S（Single）字母的SIMD指令（例如mulss），这种指令一次性也就是执行一条计算，相比普通的FPU指令提速非常有限甚至更慢，因此，优不优化速度基本没啥区别。另外一个重要的问题在论文中其实没有提及，那就是随着半径的增加，Joint Histgram中得非0元素会相对的变得越来越少（但整体比例还是很大的），但是在BCB中，只要某个固定Feature对应的LevelF个直方图元素中有一个不为0，那么他就会不为0，这个情况在大半径时发生的概率非常高，此时的更新Necklace Table的时间和后续减少计算的时间来说可能会本末倒置，反而会引起计算时间的增加。
基于这样一个分析，隐含着这样一个事实，当半径比较小时，由于计算过程中非零值的存在，Joint + MT + NT应该效果会更改，而随着半径的增加，非零值减小，NT带来的收益越来越小，甚至抵消了，我们实测了下面一组数据。
|
算法名称 |
不同半径时的执行时间（ms） |
|||||||
|
1 |
3 |
5 |
8 |
10 |
15 |
20 |
40 |
|
|
Joint + MT |
386 |
404 |
396 |
416 |
436 |
500 |
540 |
744 |
|
Joint + MT + NT |
153 |
316 |
306 |
412 |
452 |
534 |
654 |
1091 |
也就是说，在容许进行SIMD优化的情况下，当半径大于10时，建议使用Joint + MT来获得更高的效率，半径小于10时，可通过Joint + MT + NT来提供更好的速度。
从代码的简练或者内存占用方面来说，毫无疑问Joint + MT更简单，也更加节省内存，如果在现在的PC上使用该算法，我更喜欢直接使用Joint + MT算法。
这样并不是说Necklace Table不好，我反到觉得这个数据结构也是由很高的利用价值，也许可以利用到我关心的其他一些算法上，会有这比较好的效果。
另外小声的说一下，似乎这里的最终优化的时间和Brute force的时间比并没有达到100:1。
五、后续关于Joint + MT进一步优化的几个尝试
既然选中Joint + MT，我们再仔细的构思下他还没有进一步优化的余地呢，第一想到的就是，我自行内嵌SIMD指令，代码中有好几个for循环使用SIMD指令应该很容易处理，但是，经过多次改写，发现这种非常简便的for循环，我们自己内嵌的SIMD指令很难超越编译器编译后的速度，毕竟写编译器的那些专家的优化水平，不是我等能够比拟的。第一步方向选择放弃。
那么如果考虑定点话呢，一般两个像素之间的权重值是个介于0和1之间的数据，如果我们把它放大一定倍数，转换为整形，那么整个计算过程就是整形的处理，而且现在整形也可以直接使用SSE处理，同样是一次性处理4个32位整形，同浮点相比，少了几次数据类型的转换，经过测试，这样处理后速度基本没有什么大的差异，这个方法也可以放弃。
第三个想法是直方图的更新，有一种常用的直方图更新方法是特例化处理图像整体最左上角的点，然后在水平方向移动时，去除最左侧的一列信息，加上最右侧的信息，当移动到第一行最右侧的像素点时，此时的更新方向不是直接跳到第二行首像素，而是从第二行尾像素向第二行手像素进行处理，这时我们可以充分利用第一行的最右侧像素的直方图数据，只要减去最上部一行的直方图信息，然后加上最下部一行的直方图的信息就可以了，在逆向移动时，直方图的更新则和第一行的更新相反，加上左侧的信息，然后减去右侧信息，当处理到第二行首地址像素后，我们又跳到第三行首地址，然后进行类似第一行的处理，这种处理方式能够减少对每行首像素进行全部直方图更新的计算量，在半径较大时有一定的加速作用，我们一般称之为蛇形算法。实验了一下，对算法的速度提升非常有限，而且会使得代码稍显繁琐。也需要放弃。
那么目前我想到的唯一的有可能对速度还有提升的就是定点化时不用32位的数据，适当的考虑数据的范围，如果能保证定点后的数据能在16位的有效范围，那么还是有可能进一步提高点速度的，毕竟这个时候可以使用SSE单指令一次性进行8个整数的加减乘法了，这个有待于进一步去测试。
六、特例优化
在有些情况下甚至很多情况下，我们使用的Feature是其自身，这种情况下因为数据的特殊性，我们可以做一些特殊处理，使得算法的速度更快。
当Feature等于Input本身时，我们注意到，联合直方图中只有45度的对角线中元素有值，其他部位都为0，因此，我们可以考虑联合直方图在形式上退化为一维直方图，这个时候一个简单的代码如下所示：
int IM_WeightedMedianBlur_Special(unsigned char *Input, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius) { int Channel = Stride / Width; if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3) && (Channel != 4)) return IM_STATUS_NOTSUPPORTED; const int Level = 256; int *Histgram = (int *)malloc(Level * sizeof(int)); if (Histgram == NULL) return IM_STATUS_OUTOFMEMORY; for (int Y = 0; Y < Height; Y++) { unsigned char *LinePS = Input + Y * Stride; unsigned char *LinePD = Output + Y * Stride; memset(Histgram, 0, Level * sizeof(int)); // 全部赋值为0 for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Index = J * Stride; for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++) { Histgram[Input[Index + I]]++; } } for (int X = 0; X < Width; X++) { int IndexF = LinePS[X] * Level; float SumW = 0, HalfSumW = 0;; for (int I = 0; I < Level; I++) { SumW += Histgram[I] * Weight[IndexF + I]; } HalfSumW = SumW / 2; SumW = 0; for (int I = 0; I < Level; I++) { SumW += Histgram[I] * Weight[IndexF + I]; if (SumW >= HalfSumW) { LinePD[X] = I; break; } } if ((X - Radius) >= 0) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { Histgram[Input[J * Stride + X - Radius]]--; } } if ((X + Radius + 1) <= Width - 1) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { Histgram[Input[J * Stride + X + Radius + 1]]++; } } } } free(Histgram); return IM_STATUS_OK; }
同样是21*21的窗口，one - metalpixel的灰度图像计算用367ms左右，比上述都要快。
同样的道理，我们也可以使用BCB技术来优化，但是此时的BCB来的更简单。
int IM_WeightedMedianBlur_Special_BCB(unsigned char *Input, float *Weight, unsigned char *Output, int Width, int Height, int Stride, int Radius) { int Channel = Stride / Width; if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3)) return IM_STATUS_NOTSUPPORTED; int Status = IM_STATUS_OK; const int Level = 256; int *Histgram = (int *)malloc(Level * sizeof(int)); int *BCB = (int *)malloc(Level * sizeof(int)); if ((Histgram == NULL) || (BCB == NULL)) { Status = IM_STATUS_OK; goto FreeMemory; } for (int Y = 0; Y < Height; Y++) { unsigned char *LinePS = Input + Y * Stride; unsigned char *LinePD = Output + Y * Stride; memset(Histgram, 0, Level * sizeof(int)); // 全部赋值为0 memset(BCB, 0, Level * sizeof(int)); int CutPoint = -1; for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Index = J * Stride; for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++) { int Value = Input[J * Stride + I]; Histgram[Value]++; // 计算每行第一个点的二维直方图，直方图的水平方向为Feature坐标，垂直方向为Value坐标 BCB[Value]--; // 此时的CutPoint初始化为-1，所以+方向的数据为0，所有的都在-方向 } } for (int X = 0; X < Width; X++) { float BalanceWeight = 0; int IndexF = LinePS[X] * Level; // 中心点P的Value所对应的那一行Feature权重起始索引 for (int I = 0; I < Level; I++) // BCB[I]中保存的是以CutPoint为分界线，Feature为I时，分界线左侧的所有Value[0-CutPoint]值的数量和分界线右侧所有的Value（CutPoint， LevelV - 1]值数量的差异 { BalanceWeight += BCB[I] * Weight[IndexF + I]; // 因为Feature为固定值时，如果中心点固定，那么不管与Feature对应的Value值时多少，Weight就是定值了。 } if (BalanceWeight < 0) // 第一个点的BalanceWeight必然小于0 { for (; BalanceWeight < 0 && CutPoint != Level - 1; CutPoint++) { int Index = CutPoint + 1; // 新的直方图的位置 BCB[Index] += Histgram[Index] * 2; // 数量是同样的道理 BalanceWeight += 2 * Histgram[Index] * Weight[IndexF + Index]; } } else if (BalanceWeight > 0) // 如果平衡值大于0，则向左移动中间值 { for (; BalanceWeight > 0 && CutPoint != 0; CutPoint--) { BCB[CutPoint] -= Histgram[CutPoint] * 2; BalanceWeight -= 2 * Histgram[CutPoint] * Weight[IndexF + CutPoint];; } } LinePD[X] = CutPoint; if ((X - Radius) >= 0) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) // 即将移出的那一列数据 { int Value = Input[J * Stride + X - Radius]; Histgram[Value]--; if (Value <= CutPoint) // 如果移出的那个值小于当前的中值 BCB[Value]--; else BCB[Value]++; } } if ((X + Radius + 1) <= Width - 1) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X + Radius + 1]; Histgram[Value]++; if (Value <= CutPoint) // 如果移出的那个值小于当前的中值 BCB[Value]++; else BCB[Value]--; } } } } FreeMemory: if (Histgram != NULL) free(Histgram); if (BCB != NULL) free(BCB); return Status; }
同样是21*21的窗口，one - metalpixel的灰度图像计算用242ms左右。
如果我们进一步退化，将其退化为普通的中值滤波，即所有Weight都相同，则删减不需要的相关代码后，可以有如下过程：
int IM_MedianBlur(unsigned char *Input, unsigned char *Output, int Width, int Height, int Stride, int Radius) { int Channel = Stride / Width; if ((Input == NULL) || (Output == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 0) || (Height <= 0) || (Radius <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3)) return IM_STATUS_NOTSUPPORTED; int Status = IM_STATUS_OK; const int Level = 256; int *Histgram = (int *)malloc(Level * sizeof(int)); if ((Histgram == NULL)) { Status = IM_STATUS_OK; goto FreeMemory; } for (int Y = 0; Y < Height; Y++) { unsigned char *LinePS = Input + Y * Stride; unsigned char *LinePD = Output + Y * Stride; memset(Histgram, 0, Level * sizeof(int)); // 全部赋值为0 int CutPoint = -1; int Balance = 0; for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Index = J * Stride; for (int I = IM_Max(0 - Radius, 0); I <= IM_Min(0 + Radius, Width - 1); I++) { int Value = Input[J * Stride + I]; Histgram[Value]++; // 计算每行第一个点的二维直方图，直方图的水平方向为Feature坐标，垂直方向为Value坐标 Balance--; } } for (int X = 0; X < Width; X++) { if (Balance < 0) // 第一个点的Balance必然小于0 { for (; Balance < 0 && CutPoint != Level - 1; CutPoint++) { Balance += 2 * Histgram[CutPoint + 1]; } } else if (Balance > 0) // 如果平衡值大于0，则向左移动中间值 { for (; Balance > 0 && CutPoint != 0; CutPoint--) { Balance -= 2 * Histgram[CutPoint]; } } LinePD[X] = CutPoint; if ((X - Radius) >= 0) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) // 即将移出的那一列数据 { int Value = Input[J * Stride + X - Radius]; Histgram[Value]--; if (Value <= CutPoint) // 如果移出的那个值小于当前的中值 Balance--; else Balance++; } } if ((X + Radius + 1) <= Width - 1) { for (int J = IM_Max(Y - Radius, 0); J <= IM_Min(Y + Radius, Height - 1); J++) { int Value = Input[J * Stride + X + Radius + 1]; Histgram[Value]++; if (Value <= CutPoint) // 如果移出的那个值小于当前的中值 Balance++; else Balance--; } } } } FreeMemory: if (Histgram != NULL) free(Histgram); return Status; }
同样是21*21的窗口，one - metalpixel的灰度图像计算用140ms左右。
有兴趣的朋友还可以试下对上述中值模糊的代码在加上Necklace table优化，看看能得到什么样的结果。
在论文的最后，讲述了加权中值模糊的多个应用场景，比如在光流、立体匹配、JPG瑕疵修复、艺术特效等等方面，我测试下几个我能做的测试，确实有不错的效果，比如下面的JPG瑕疵修复。对简单的图处理后确实蛮好的，如果在结合我之前研究的MLAA去锯齿算法，恢复后的图像质量就更高了，如下所示：
原图 加权中值模糊（特征图为原图） MLAA后续处理后（边缘更平滑）
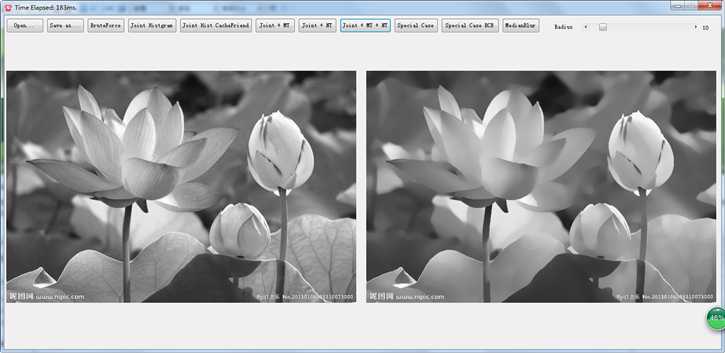
另外，WMF的保边特性感觉比其他的如导向滤波、双边滤波等等都要强烈的多，比如下图：
花朵的边缘，下面的文字等等处理都还特别清晰，不像其他的保边滤波器总有点模糊，这个特性也许用到一些增强上也会有很不错的效果。
按照上述文章的思路，我整理和编制一个简易的测试程序，用来论证论文和我博文中得一些数据，使用的VS2013编译的，用C++做的DLL，C#做的UI测试界面，不依赖于任何其他第三方库，目前只做了灰度图的方案，因为彩色的话也基本就是三个通道独立写，可以通过拆分然后调用灰度的来实现。我也测试了下作者分享的VS工程，应该比我提供的代码速度稍微慢一点。
源代码下载地址：https://files.cnblogs.com/files/Imageshop/WeightedMedianBlur.rar
以上是关于CVPR论文《100+ Times Faster Weighted Median Filter (WMF)》的实现和解析（附源代码）。的主要内容，如果未能解决你的问题，请参考以下文章
CVPR 2018Domain Adaptive Faster R-CNN for Object Detection in the Wild