



我们在用二维树状数组的时候,可以得到一个边与坐标轴平行的矩形内点集的信息。
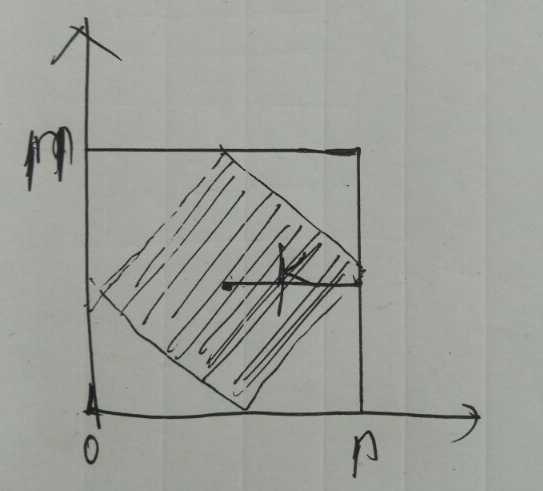
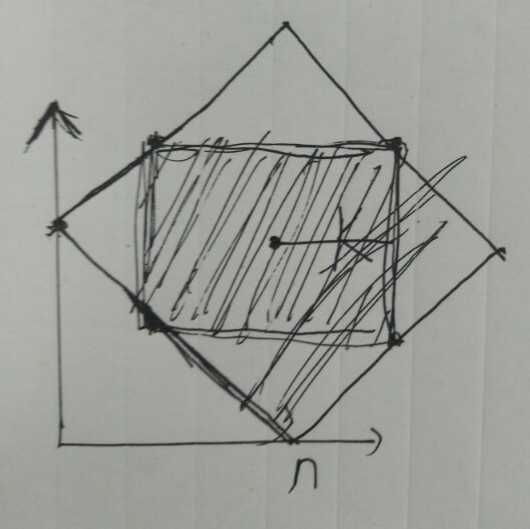
如果我们需要得到得到到一个点的距离小于等于K的点的信息呢。这些点构成的不在是边也坐标轴平行的矩形,而是一个对角线与坐标轴平行的菱形。
可以通过转化,使得整个坐标轴旋转45°,然后我们菱形变成了方方正正的矩形,又可以用而二维树状数组或者直接用前缀和来得到矩形区间信息。
旋转后区域边长*√2,面积*2,原本的距离<=K的区域,现在变成了[x’-k,y’-k]到[x’+k,y’+k]的矩形区域。我们假设顺时针旋转45°。
怎么转化呢?为了避免用公式的时候出错,我们一竖一竖的旋转:
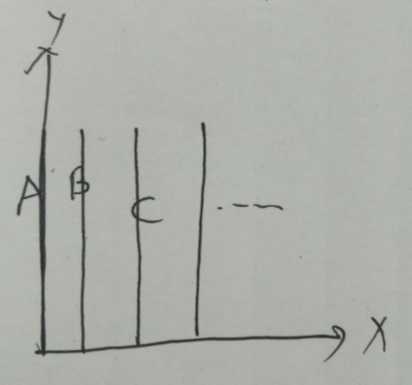
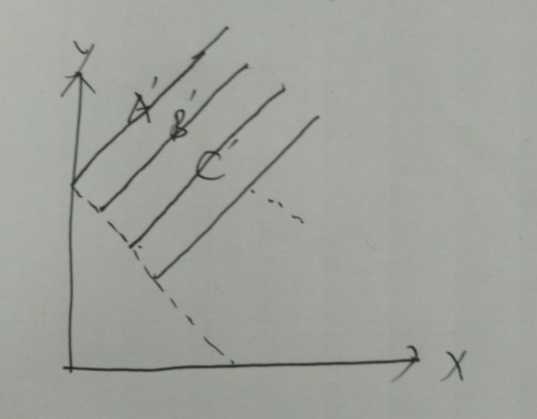
对于每一竖,我们得到(x,0)对应的(x,n-x+1),然后向上一个个移动,等效于向右上一个一个移动。
则有:
for(int i=1;i<=n;i++){ int x=i,y=n-i+1; for(int j=1;j<=n;j++) b[x++][y++]=a[i][j]; }
注意, 为了避免K太大,而超出边界,而边界外的点没有可用信息,我们需要判断一下边界。
void stardard(int &x) { x=max(x,1); x=min(x,2*n-1); }
所以想要得到信息的时候,也同样转化坐标:
int x1=x,y1=n-x+1; x1+=y-1;y1+=y-1; int ans+=getSum(i,x1-k,y1-k,x1+k,y1+k);
(里面记住缩小边界)
那么根本不用记公式(虽然公式不难)。切比雪夫转曼哈顿的话,也只需要一个一个转就行了。不好处理边界的话,可以每个点的横纵坐标都加一个值,防止越界。
感觉还是比较常用的,所以例题就不说了。