MySQL B+树结构解析以及深度计算

Posted 2023-03-06 _雪辉_

文章目录

• • • 一、MySQL的索引结构
    • • 1.1 MySQL索引结构与B+树
      • 1.2 B+树增删数据图解
    • 二、MySQL数据页
    • • 2.1 索引高度h与页面I/O数的关系
      • 2.2 索引高度理论计算
    • 三、查看MySQL树高

一、mysql的索引结构

1.1 MySQL索引结构与B+树

  MySQL使用B+树存储索引数据，B+树的非叶节点不保存数据相关信息， 只保存关键字和子节点的引用；关键字对应的数据保存在叶子节点中；B+树的叶子节点是顺序排列的，且相邻接点具有顺序引用关系，因此B+树在范围查找时能力更强，同时排序能力更强。因为仅仅在叶子节点存储数据，这样索引文件更小，磁盘读写能力更强。B+树的树高较低，索引文件较小，IO次数稳定，查询效率更加稳定。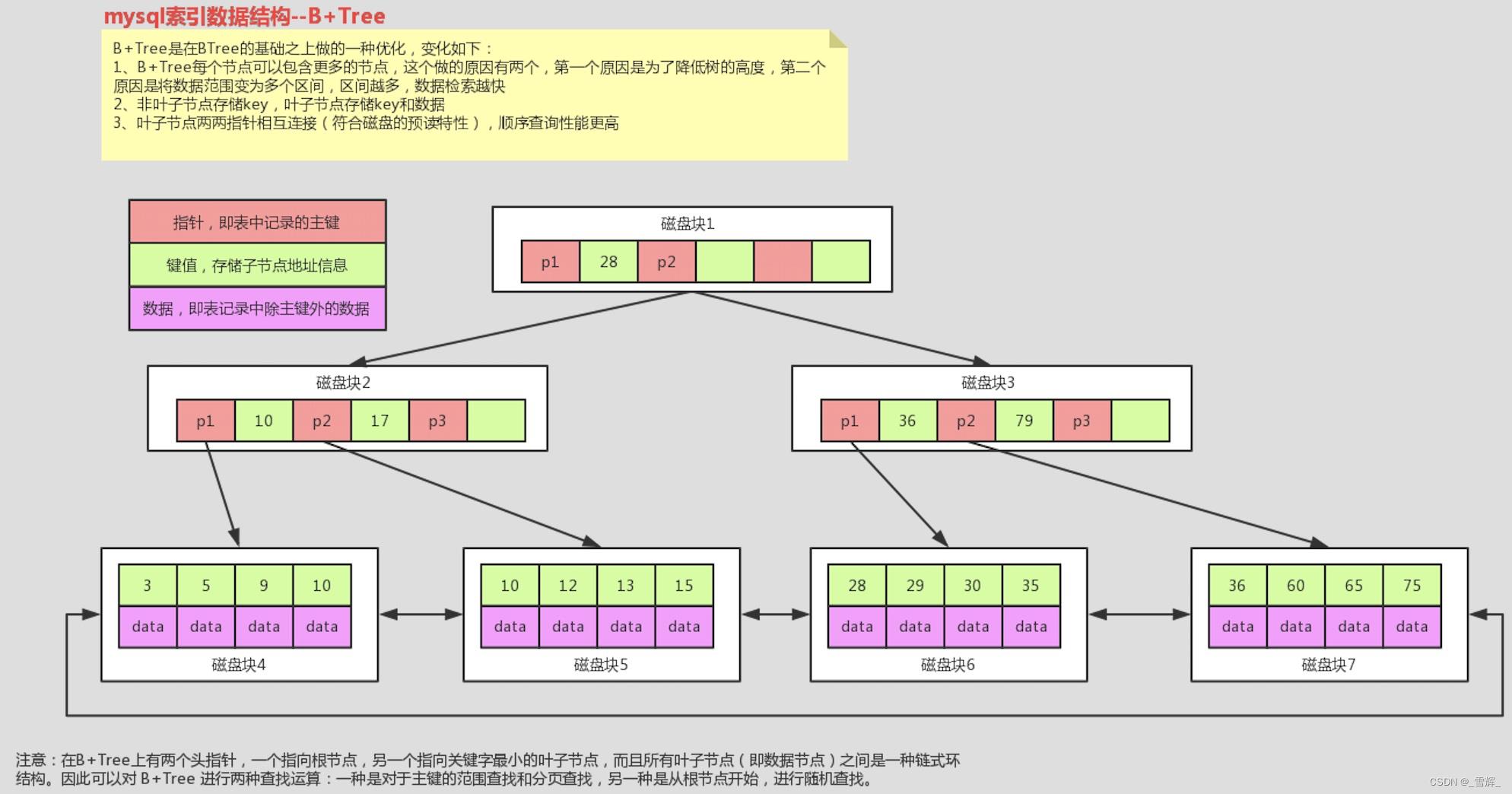
**数据就存在主键索引的叶子节点中，其他索引存主键，再从主键索引中找数据；InnoDB是通过B+树结构对主键创建索引，然后叶子节点中储存记录，如果没有主键，那么会选择唯一键，如果没有唯一键，那么会生成一个6位的row_id来作为主键。如果创建索引的键是其他字段，那么在叶子节点中存储的是该记录的主键，然后再通过主键索引找到对应的记录。　**

1.2 B+树增删数据图解

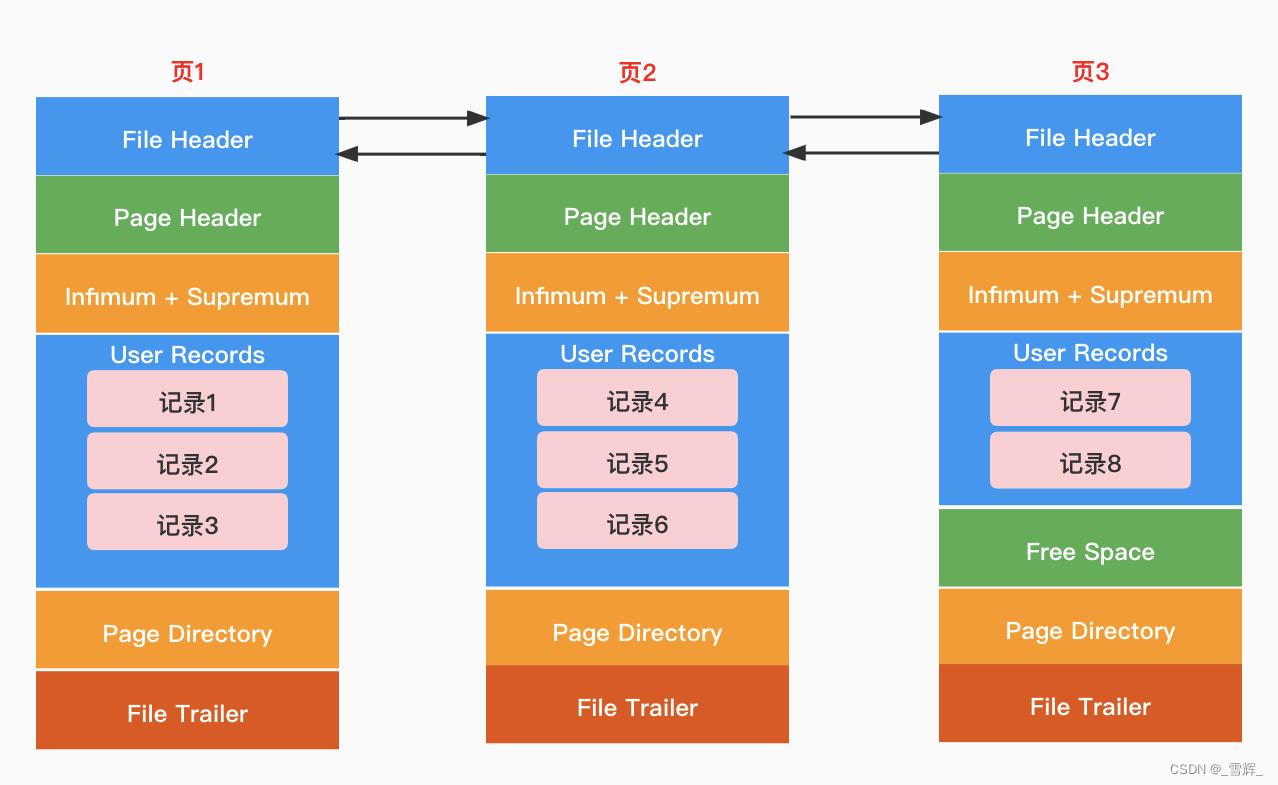
二、MySQL数据页

  MySQL的InnoDB是以页为存储单位的，每个B+Tree的节点都是一个页的大小，默认一页的大小是16K。

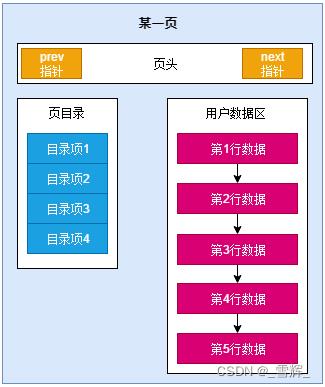
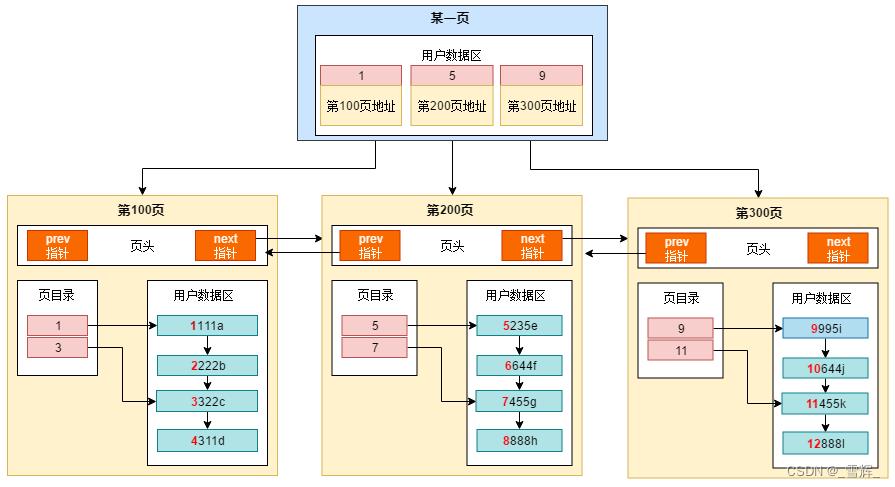
2.1 索引高度h与页面I/O数的关系

  MySQL每次查询都要访问到叶子结点，其访问的页面数正好就是索引的高度h。例如，一次主键上的点查询select * from table_name where id=1;，那么要查询h1个页面才能找到叶子结点里的行数据，也即进行h1次页面I/O。查询对应的页面I/O数跟利用的索引有关，主要分为以下几种情况：

• 点查询：

  • 聚族索引：h1
  • 二级索引：
    • 覆盖索引：h2
    • 回表查询：h2+h1

• 范围查询：h1 - 1 + 叶子结点数量

• 全表查询：B+树的叶子结点是通过链表连接起来的，对于全表查询，需要从头到尾将所有的叶子结点访问一遍。

2.2 索引高度理论计算

  索引页（非叶子节点）中可以分割为多个扇区，每个扇区再指向某子节点（某页）；
假设非叶子节点扇区数为k个、高度h、叶子结点的行记录数为n，则叶子结点数为k(h-1)，总记录数为k(h-1)*n。
假设主键ID为bigint类型，长度为8字节，而指针大小在InnoDB源码中设置为6字节，这样一共14字节。 那么一个页中能存放多少这样的组合，就代表有多少指针，即 16384 / 14 = 1170。那么可以算出一棵高度为2 的B+树，能存放 1170 * 16 = 18720 条这样的数据记录。在高度h=3时，叶子结点数=1170^2 ≈137W，总记录数=1170^2*16=2190W；也就是说，InnoDB通过三次索引页面的I/O，即可索引2190W行记录；同理，在高度h=4时，总行数=1170^3*16≈256亿条

三、查看MySQL树高

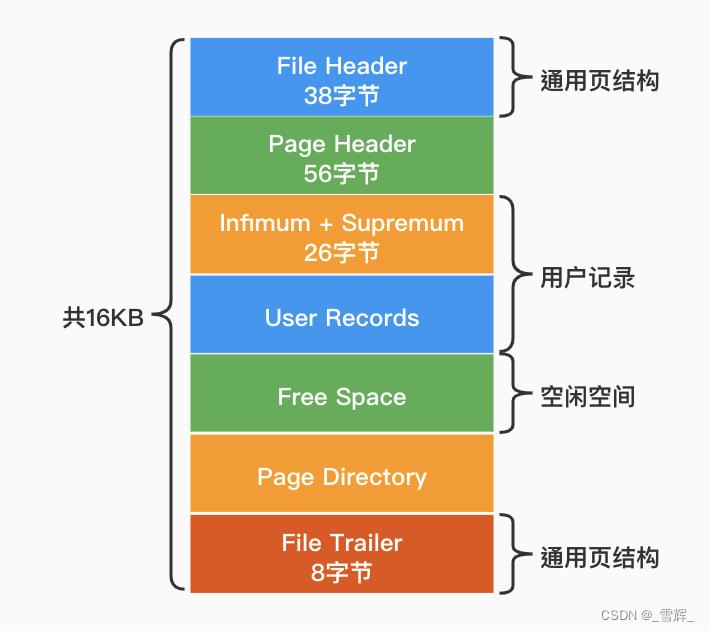
  页的Page Header包含一个PAGE_LEVEL的信息，用于表示当前页所在索引中的高度。默认叶子节点的高度为0，那么Root页（根节点）的PAGE_LEVEL+1就是这棵索引的高度。每张表的根页位置在表空间文件中是固定的，即page number=3的页，找到根页后通过二分查找法，定位到数据在指针指向的页中，然后再去数据页中查找，同样通过二分查询法即可找到记录。

SELECT b.name, a.name, index_id, type, a.space, a.PAGE_NO
FROM information_schema.INNODB_SYS_INDEXES a,
     information_schema.INNODB_SYS_TABLES b
WHERE a.table_id = b.table_id 
      AND a.space <> 0;

  PAGE_NO代表ibd文件中的页面号（从0开始）。PAGE_LEVEL在每个Root页的偏移量64位置处，占用两个字节，这样我们通过hexdump就可以快速定位到各索引树的高度信息。主键索引B+树的根页在整个表空间文件中的第3个页开始，所以算出它在文件中的偏移量；16384*3+64=49216 ：即从第3个页内偏移量64位置开始读取10个字节，前两个字节为PAGE_LEVEL，后8个字节是index_id。

#00 01,所以树高为1+1=2
hexdump -C -s 49216 -n 10 table.ibd
0000c040  00 01 00 00 00 00 00 00  03 2b