1.1图的基本概念

Posted 2021-01-13 s-way

（参考书籍：2018数据结构 王道考研）

图的定义

图G由定点集V和边集E组成

记为G=(V,E)

其中V(G)为G中顶点的有限非空集

E(G)为G中边（顶点关系）集和

|V|表示G中顶点个数，也称为图的阶

E={ (u , v) | u, v 均为顶点 } |E|表示G中边的条数

 

注意：图不能为空，边可以为空，但顶点一定非空

 

有向图

若E为有方向的边（也称为弧），此时图为有向图

记做<u，v > u为弧头 v为弧尾，称为u到v的弧、u邻接到v的弧、v邻接自u的弧

 

 

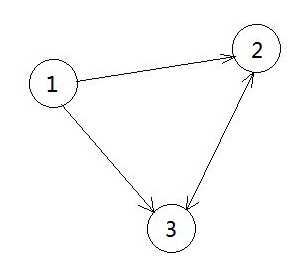
G = (E , V)

E = {1,2,3}

V = {<1, 2>, <1, 3>, <2, 3>, <3, 2>}

 

无向图

E为无向边 （简称边），则图为无向图

记为（u, v）or （v, u）　　此时（u, v）==（v, u） 因为无向

 

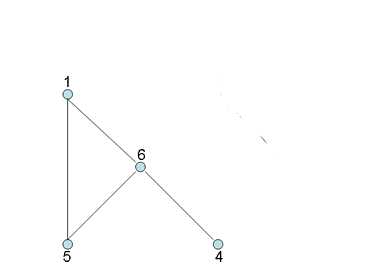
G = (V, E)

V = {1, 4, 5, 6} 

E = {(1, 6), (1, 5), (5, 6), (4, 6)}

 

 简单图

满足下列条件：

1.无重复边

2.无顶点到自身的边，上面两个图都是简单图

 

多重图

与简单图相反：

1.存在重复边

2.允许顶点通过一条边与自己相连

 

完全图

无向完全图：任意两个点之间存在边

有向完全图：任意两个点之间存在反方向的两条弧

 

子图

G = (V, E)　　G‘ = (V‘ , E‘)

V‘ 、E‘ 是 V 、E 的子群那么G‘ 是G 的子图,若V(G‘) = V(G),则G‘为G的生成子图

连通、连通图和连通分量（无向图）

 顶点v 到 顶点w 有路径存在，则称v 和 w 是连通的。若图G中任意两个顶点都是连通的，则称G为连通图，否则称为非连通图。

无向图的极大连通子图称为连通分量

 极大连通子图：无向图的连通分量，要求子图包含所有的边。

 极小连通子图：保持连通，并且边数最少的子图。

 

强连通图、强连通分量（有向图）

v->w w->v 均由路径，则称这两个顶点是强连通的

若图中任意一对顶点都是强连通的，那么这个图是强连通图

极大连通子图称为该图的强连通分量。

 

生成树、生成森林（连通图）

连通图的生成树：包含途中全部顶点的一个极小连通子图。

非连通图，连通分量的生成树构成非连通图的生成森林

 

顶点的度、入度和出度

设e为边（edge）、v为依附于某一顶点的边的条数

无向图：Sum（TD(vi)） = 2e

有向图：TD(v) = ID(v) + OD(v)， sum（ID(vi)）+ sun（OD(vi)） = e

 

边的权和网

在图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值

这种边上带有权值的图称为带权图（网）

 

稠密图、稀疏图

边数很少的图，称之为稠密图。

此时边数目，通常满足：|E| < |V| * log |V|

 

路径、路径长度和回路

路径：指的是图中顶点到顶点的顶点序列

路径长度：路径上边的数目

回路、环：第一个顶点和最后一个顶点相同的路径

 

简单路径、简单回路

简单路径：该路径中无重复顶点

简单回路：仅顶点重复，其他顶点无重复

 

距离

u 到 v 的最短路径

u 到 v 不存在路径 记做 无穷

 

有向树

有一个顶点的入度为0，其他顶点入度为1的图称作有向树。