图论:图的基本概念
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图论:图的基本概念相关的知识,希望对你有一定的参考价值。
图论(1):图的基本概念
一.无向图
1.无向图定义
设V是一个非空集合, V 的一切二元子集之集合记为 P 2 ( V ) P_2(V) P2(V), 即 P 2 ( V ) = { A ∣ A ⊆ V , ∣ A ∣ = 2 } P_2(V)=\\{A|A\\subseteq V,|A|= 2 \\} P2(V)={A∣A⊆V,∣A∣=2}
设 E ⊆ P 2 ( V ) , E\\subseteq P_2(V), E⊆P2(V),二元组 ( V , E ) (V,E) (V,E)称为一个无向图,V 中元素称为无向图的顶点,V 为顶点集;E 称为边集,E 的元素称为图的边, 如果 { u , v } ⊆ E \\{u,v\\}\\subseteq E {u,v}⊆E ,则称u 与v 邻接
2.无向图术语
①简单图
每个顶点都没有圈,任意两个顶点间最多只有一条边,任意一条边都可用它的两个端点来表示:
常用小写的英文字母 u,v,w 表示图的顶点( ( 可以带下标 );
常用小写的英文字母 x,y,z 表示图的边( ( 可以带下标) )
②(p,q)图
如果|V|= p, |E|= q ,则称G 为一个(p, q) 图,即G 是一个具有p 个顶点q 条边的图
(1,0)图又称为平凡图
③顶点与边的关联, 边与边邻接
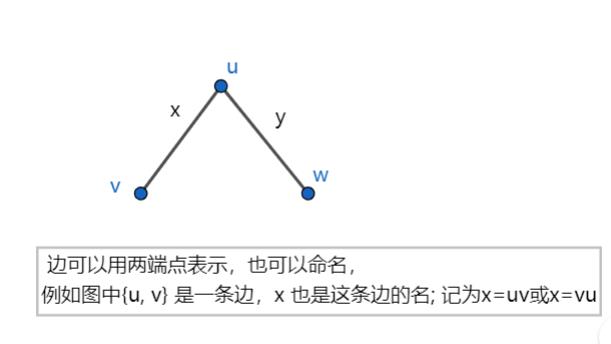
- 称u 和v 为边x 的端点
- 称顶点u 和v 与边x 互相关联
- 称u 和v 邻接
- 若 x 与y 是图G 的两条边, 并且仅有一个公共端点,即 即|x∩y|=1,则称边x 与y邻接
④图的关系表示
由定义可知, 一个无向图G 就是一个非空集合V 上定义的一个 反自反且对称的二元关系E 和V 构成的系统
⑤带环图
联结一个顶点与其自身的边称为环,允许有环存在的图称为带环图
⑥多重边图
如果允许两个顶点之间有两个以上的边存在,这样的边称为多重边,允许有环与多重边存在的图,我们称为 伪图
⑦零图
设G=(V,E)为无向图,如果E= ϕ \\phi ϕ,则称G为零图
n 个顶点的零图称为n 阶零图
⑧完全图
设 G=(V,E) 为无向图, , 如果G 中任意两个顶点间都有唯一的边, 则称G为完全图
n个顶点的完全图用 K n K_n Kn表示, K n K_n Kn共 C n 2 = n ( n − 1 ) 2 ( n ≥ 2 ) C_n^2=\\frac{n(n-1)}{2}(n\\geq2) Cn2=2n(n−1)(n≥2)条边
二.有向图
1.有向图定义
设V为一个非空有限集, A ⊆ V × V ∖ { ( u , u ) ∈ V } A\\subseteq V\\times V\\setminus \\{ (u,u) \\in V \\} A⊆V×V∖{(u,u)∈V}, 二元组D=(V, A) 称为一个有向图,V 中的元素称为D 的顶点,A 中元素(u,v) 称为D 的从u 到v 的弧或有向边
2.有向图术语
弧:有向图的边
对称弧:
如果 x=(u,v) 与 y=(v,u) 均为A的弧, , 则称 x 与y 为一对对称弧. .
起点,终点:
如果 x=(u,v) 是有向图的一条边, , 则称弧x 为起于顶点u 终于顶点v 的弧, , 或从u到v的弧 ,u 称为x 的起点 ,v 为终点
定向图:不含对称弧的有向图
三.子图
1.子图
设G = (V, E) 是一个图, 图 H = ( V 1 , E 1 ) H=(V_1,E_1) H=(V1,E1)称为G 的一个子图, 其中 V 1 V_1 V1是V 的非空子集且 E 1 E_1 E1是E的子集
2.真子图
设 G 1 G_1 G1和$G_2 是 图 是图 是图G$ 的两个子图,如果 G 1 ≠ G G1\\ne G G1=G, 则称 G 1 G_1 G1是 G G G 的真子图。
3.生成子图
①定义
设G=(V,E) 是一个图, 如果 F ⊆ E F\\subseteq E F⊆E, 则称
G 的子图H=(V, F) 为G的生成子图
生成:包含所有顶点
②表示
设x 是G 的一条边, 则G 的生成子图(V,E\\{x}) 简记为G-x
如果u 和v 是G 的两个不邻接的顶点, 则图(V,E ∪{u,v}) 简记成G+uv, 它是在G 的图解中, 把u 与v 间联一条线而得到的图
4.极大子图
设G的子图H 具有某种性质,若G中不存在与H不同的具有此性质且包含H 的真子图, 则称H 是具有此性质的极大子图
5.导出子图
①定义
设S为图G=(V,E)的顶点集V的非空子集,则G 的以S 为顶点集的极大子图称为由S 导出的子图,记 记为<S>. 形式地,<S>=(S, P 2 ( S ) ∩ E ) \\mathrm{P_2 (S)∩E}) P2(S)∩E).
于是,S 的两个顶点在<S> 中邻接, 当且仅当这两个顶点在G中邻接
②表示
设G=(V,E),由V{v} 导出的子图<V{v}> 记成G-v,从图的图解上看,G-v 的图解是从G 的图中去掉顶点v 及与v关联的边所得到的图解
六.图的同构
1.定义
设 G=(V,E),H=(U,F) 是两个无向图,如果存在一个一一对应 φ : V → U \\varphi:V\\rightarrow U φ:V→U, 使得 u v ∈ E uv\\in E uv∈E 当且仅当 φ ( u ) φ ( v ) ∈ F \\varphi(u)\\varphi(v)\\in F φ(u)φ(v)∈F, 则称G G与H同构, , 记为 G ≅ H G\\cong H G≅H
七.顶点的度
1.定义
设v为图 G=(V,E) 的任一顶点 ,G 中与v 关联的边的数目称为顶点v 的度,记为 degv
2.定理(欧拉)
设 G=(V,E) 是一个具有p个顶点q条边的图, , 则G中各顶点度的和等于边的条数q的两倍, , 即 ∑ v ∈ V d e g v = 2 q \\sum\\limits_{v\\in V}degv=2q v∈V∑degv=2q
推论1:任一图中, 度为奇数的顶点的数目必为偶数
3.定义(正则图)
先定义最大度、最小度:显然, 对(p,q) 图的每个顶点v, 有0≤degv≤p-1, δ ( G ) = min v ∈ V { d e g v } , Δ ( G ) = max v ∈ V { d e g v } \\delta(G)=\\min\\limits_{v\\in V}\\{degv\\},\\Delta(G)=\\max\\limits_{v\\in V}\\{degv\\} δ(G)=v∈Vmin{degv},Δ(G)=v∈Vmax{degv}
若 δ ( G ) = Δ ( G ) = r \\delta(G)=\\Delta(G)=r δ(G)=Δ(G)=r,则图G称为r度正则图,即G 的每个顶点的度都等于r,3 度正则图也叫做三次图, 一个具有p个顶点的p-1 度正则图称为p 个顶点的完全图, 记为 K p K_p Kp 。
推轮2:每个三次图有偶数个顶点,度为零的顶点称为弧立顶点 ,0 度正则图就是零图
八.路、圈、连通图
1.通道、闭通道
①定义(通道:交错序列)
设G = (V , E)是一个图,G的一条通道时G的顶点和边的一个交错序列 v 0 , x 1 , v 1 , x 2 … , v n − 1 , x n , v n v_0,x_1,v_1,x_2…,v_{n−1},x_n,v_n v0,x1,v1,x2…,vn−1,xn,vn
其中 x i = v i − 1 v i , i = 1 , 2 , . . . , n x_i=v_{i-1}v_i,i=1,2,...,n xi=vi−1vi,i=1,2,...,n,n称为通道的长,这样的通道常常称为 v 0 − v n \\mathrm{v_0-v_n} v0−vn通道,并简记为 v 0 v 1 v 2 . . . v n \\mathrm{v_0v_1v_2...v_n} v0v1v2...以上是关于图论:图的基本概念的主要内容,如果未能解决你的问题,请参考以下文章