题解报告——森林

Posted 2021-01-12 genius777

题目传送门

题目描述

小Z有一片森林，含有N个节点，每个节点上都有一个非负整数作为权值。初始的时候，森林中有M条边。

小Z希望执行T个操作，操作有两类：

1. Q x y k查询点x到点y路径上所有的权值中，第k小的权值是多少。此操作保证点x和点y连通，同时这两个节点的路径上至少有k个点。
2. L x y在点x和点y之间连接一条边。保证完成此操作后，仍然是一片森林。

为了体现程序的在线性，我们把输入数据进行了加密。设lastans为程序上一次输出的结果，初始的时候lastans为0。

• 对于一个输入的操作Q x y k,其真实操作为Q x^lastans y^lastans k^lastans。
• 对于一个输入的操作L x y，其真实操作为L x^lastans y^lastans。其中^运算符表示异或，等价于pascal中的xor运算符。

请写一个程序來帮助小Z完成这些操作。

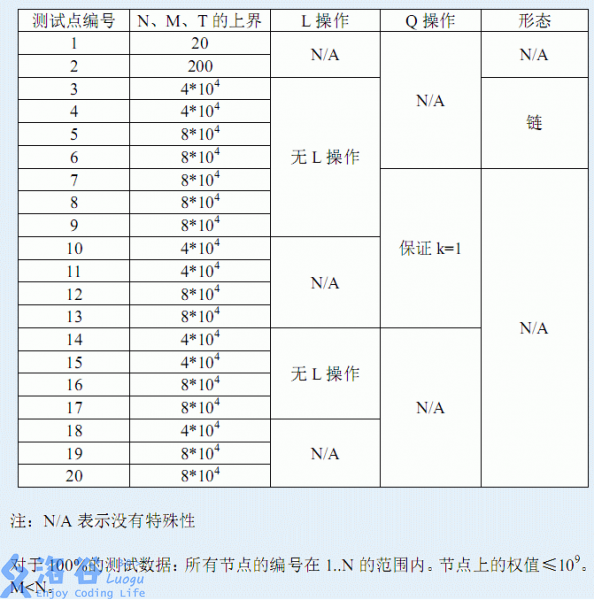
对于所有的数据，n,m,T<=8∗1048*10^48∗104.

输入输出格式

输入格式：

 

第一行包含一个正整数testcase，表示当前测试数据的测试点编号。保证1<=testcase<=20。

第二行包含三个整数N，M，T，分别表示节点数、初始边数、操作数。

第三行包含N个非负整数表示 N个节点上的权值。

接下来 M行，每行包含两个整数x和 y，表示初始的时候，点x和点y 之间有一条无向边。

接下来 T行，每行描述一个操作，格式为”Q x y k“或者”L x y “，其含义见题目描述部分。

 

输出格式：

 

对于每一个第一类操作，输出一个非负整数表示答案。

 

输入输出样例

输入样例#1： 复制

1
8  4 8
1  1 2 2 3 3 4 4
4  7
1  8
2  4
2  1
Q 8 7 3 Q 3 5 1
Q 10 0 0
L 5 4
L 3 2 L 0 7
Q 9 2 5 Q 6 1 6

输出样例#1： 复制

2 
2
1
4
2

说明

对于第一个操作 Q 8 7 3，此时 lastans=0，所以真实操作为Q 8^0 7^0 3^0，也即Q 8 7 3。点8到点7的路径上一共有5个点，其权值为4 1 1 2 4。
这些权值中，第三小的为 2，输出 2，lastans变为2。

对于第二个操作 Q 3 5 1 ，此时lastans=2，所以真实操作为Q 3^2 5^2 1^2 ，也即Q 1 7 3。点1到点7的路径上一共有4个点，其权值为 1 1 2 4 。
这些权值中，第三小的为2，输出2，lastans变为 2。之后的操作类似。

---

【思路分析】

一看就是大力数据结构，没啥可说的，就是树上主席树带一个启发式合并，复杂度O(nlog^2)，离散化后即可AC

 但是比较坑爹的是这里的T是测试点编号，不是数据组数，害得我TLE了一上午。。。垃圾出题人

---

 【代码实现】

  1 #include<cstdio>
  2 #include<cctype>
  3 #include<cstring>
  4 #include<algorithm>
  5 #include<vector>
  6 using namespace std;
  7 typedef long long ll;
  8 void read(int &v)
  9 {
 10     int f;char ch;
 11     while(!isdigit(ch=getchar())&&ch!=‘-‘); ch==‘-‘?(f=-1,v=0):(f=1,v=ch-‘0‘);
 12     while(isdigit(ch=getchar())) v=v*10+ch-‘0‘;v=v*f;
 13 }
 14 const int N=8e4+5;
 15 struct sd{
 16     int son[2],sum;
 17 }t[N*200];
 18 struct e{
 19     int next,to;
 20     e(){};
 21     e(int a,int b){next=a,to=b;}
 22 }edge[N<<1];
 23 int head[N],val[N],tmp[N],root[N],siz[N],up[N][18],rt[N],dep[N];
 24 int n,m,q,T,cur,cnt,tot,lastans;
 25 void clear()
 26 {
 27     cnt=0,cur=0,tot=0,lastans=0;
 28     memset(head,0,sizeof(head));
 29     memset(rt,0,sizeof(rt));
 30     memset(siz,0,sizeof(siz));
 31     for(int i=1;i<=n;i++) root[i]=i,up[i][0]=0;
 32 }
 33 void insert(int &v,int vv,int l,int r,int pos)
 34 {
 35     v=++cnt;
 36     t[v]=t[vv],t[v].sum++;
 37     if(l==r) return;
 38     int mid=l+r>>1;
 39     if(pos<=mid) insert(t[v].son[0],t[vv].son[0],l,mid,pos);
 40     else insert(t[v].son[1],t[vv].son[1],mid+1,r,pos);
 41 }
 42 void dfs(int v,int ff,int rrt)
 43 {
 44     insert(rt[v],rt[ff],1,tot,val[v]);
 45     dep[v]=dep[ff]+1,up[v][0]=ff,root[v]=rrt,siz[rrt]++;
 46     for(int i=1;i<=17;i++) up[v][i]=up[up[v][i-1]][i-1];
 47     for(int i=head[v];i;i=edge[i].next)
 48     {
 49         int to=edge[i].to;
 50         if(to==ff) continue;
 51         dfs(to,v,rrt);
 52     }
 53 }
 54 void add_edge(int a,int b)
 55 {
 56     edge[++cur]=e(head[a],b),head[a]=cur;
 57     edge[++cur]=e(head[b],a),head[b]=cur;
 58 }
 59 int LCA(int a,int b)
 60 {
 61     if(dep[a]<dep[b]) swap(a,b);
 62     int len=dep[a]-dep[b];
 63     for(int i=17;i>=0;i--) if(len&(1<<i)) a=up[a][i];
 64     if(a==b) return a;
 65     for(int i=17;i>=0;i--) if(up[a][i]!=up[b][i]) a=up[a][i],b=up[b][i];
 66     return up[a][0];
 67 }
 68 int query(int v1,int v2,int v3,int v4,int l,int r,int k)
 69 {
 70     if(l==r) return tmp[l];
 71     int mid=l+r>>1,tmp=t[t[v1].son[0]].sum+t[t[v2].son[0]].sum-t[t[v3].son[0]].sum-t[t[v4].son[0]].sum;
 72     if(tmp>=k) return query(t[v1].son[0],t[v2].son[0],t[v3].son[0],t[v4].son[0],l,mid,k);
 73     else return query(t[v1].son[1],t[v2].son[1],t[v3].son[1],t[v4].son[1],mid+1,r,k-tmp);
 74 }
 75 int main()
 76 {
 77     read(T),T=1;
 78     while(T--)
 79     {
 80         int a,b,k;char opt[3];
 81         read(n),read(m),read(q);
 82         clear();
 83         for(int i=1;i<=n;i++) read(val[i]),tmp[i]=val[i];
 84         sort(tmp+1,tmp+1+n);
 85         tot=unique(tmp+1,tmp+1+n)-tmp-1;
 86         for(int i=1;i<=n;i++) val[i]=lower_bound(tmp+1,tmp+1+tot,val[i])-tmp;
 87         for(int i=1;i<=m;i++) read(a),read(b),add_edge(a,b);
 88         for(int i=1;i<=n;i++) if(root[i]==i) dfs(i,0,i);
 89         while(q--)
 90         {
 91             scanf("%s",opt),read(a),read(b),a^=lastans,b^=lastans;
 92             if(opt[0]==‘L‘){
 93                 add_edge(a,b);
 94                 if(siz[root[a]]<siz[root[b]]) swap(a,b);
 95                 dfs(b,a,root[a]);
 96             }
 97             else {
 98                 read(k),k^=lastans;
 99                 int lca=LCA(a,b);
100                 lastans=query(rt[a],rt[b],rt[lca],rt[up[lca][0]],1,tot,k);
101                 printf("%d
",lastans);
102             }
103         }
104     }
105     return 0;
106 }