前言
多题一解是思维训练的好素材。
直曲线相切
【变式】直线\\(y=x\\)上的点为\\(P(x,y)\\),函数\\(y=lnx\\)上的点是\\(Q(m,n)\\),求\\(\\sqrt{(x-m)^2+(y-n)^2}\\)的最小值。
分析:采用平行线法,
设和直线\\(y=x\\)平行且和函数\\(y=lnx\\)相切的直线为\\(y=x+m\\),
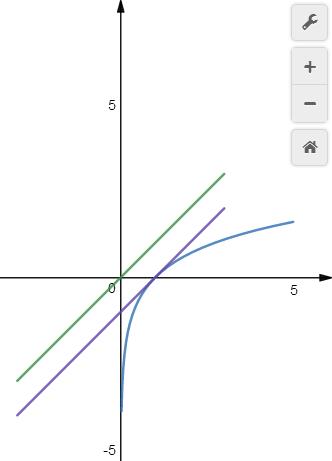
切点为\\(P_0(x_0,y_0)\\),则有
\\(\\begin{cases} y_0=x_{0}+ m \\\\ y_0=lnx_0 \\\\ f\'(x_0)=\\cfrac{1}{x_0}=1\\end{cases}\\);
从而解得\\(x_0=1,y_0=0,m=-1\\)
所以所求的点点距的最小值,就转化为切点\\(P_0(1,0)\\)到直线\\(x-y=0\\)的点线距,
\\(d=\\cfrac{|1-0|}{\\sqrt{1^2+1^2}}=\\cfrac{\\sqrt{2}}{2}\\)。
或者两条直线\\(y=x,y=x-1\\)的线线距\\(d=\\cfrac{|1-0|}{\\sqrt{1^2+1^2}}=\\cfrac{\\sqrt{2}}{2}\\)。课件地址
能成立问题
【法1】:分离参数,得到\\(a≥\\cfrac{2}{x}-x\\)在区间\\([1,5]\\)上能成立,
转化为求新函数\\(\\cfrac{2}{x}-x\\)在\\([1,5]\\)上的最小值。
令\\(g(x)=\\cfrac{2}{x}-x,g(x)=\\cfrac{2}{x}-x\\)在区间 \\([1,5]\\)上单调递减,
所以\\(g(x)_{min}=g(5)=-\\cfrac{23}{5}\\),所以\\(a≥-\\cfrac{23}{5}\\),
即\\(a\\)的取值范围是\\([-\\cfrac{23}{5},+\\infty)\\)
【法2】:转化为求\\(x\\in [1,5]\\)上的\\(f(x)_{max}\\ge 0\\),
对称轴是\\(x=-a\\),针对\\(x=-a\\)和给定区间的位置关系分类讨论即可,较繁琐,
①当\\(-a\\leq 1\\)时,即\\(a\\ge -1\\)时,\\(f(x)\\)在区间\\([1,5]\\)单调递增,
故\\(f(x)_{max}=f(5)=5a+23\\ge 0\\),即\\(a\\ge -\\cfrac{23}{5}\\),
又由于\\(a\\ge -1\\),求交集得到\\(a\\ge -1\\);
②当\\(1<-a<5\\)时,即\\(-5<a<-1\\)时,\\(f(x)\\)在区间\\([1,5]\\)有减有增无单调性,
\\(f(x)_{max}=max{f(1),f(5)}\\),
\\(f(1)=a-1\\),\\(f(5)=5a+23\\),
\\(f(5)-f(1)=4a+24\\in [4,20]\\),即\\(f(5)>f(1)\\),
故\\(f(x)_{max}=f(5)=5a+23\\ge 0\\),即\\(a\\ge -\\cfrac{23}{5}\\),
求交集得到,\\(-\\cfrac{23}{5}\\leq a<-1\\);
③当\\(-a\\ge 5\\)时,即\\(a\\leq -5\\)时,\\(f(x)\\)在区间\\([1,5]\\)单调递减,
故\\(f(x)_{max}=f(1)=a-1\\ge 0\\),即\\(a\\ge 1\\),
求交集得到\\(a\\in \\varnothing\\);
综上所述,得到\\(a\\in [-\\cfrac{23}{5},+\\infty)\\)。
即\\(a\\)的取值范围是\\([-\\cfrac{23}{5},+\\infty)\\)
【法3】:转化为不等式\\(f(x)=x^2 +ax-2≥0\\)在区间 \\([1,5]\\)上有解,
解法基本同于法2,
①当\\(-a\\leq 1\\)时,必须\\(f(5)\\ge 0\\),解得\\(a\\ge -1\\);
②当\\(1<-a<5\\)时,必须\\(f(5)\\ge 0\\),解得\\(-\\cfrac{23}{5}\\leq a<-1\\);
③当\\(-a\\ge 5\\)时,必须\\(f(1)\\ge 0\\),解得\\(a\\in \\varnothing\\);
综上所述,得到\\(a\\in [-\\cfrac{23}{5},+\\infty)\\)。
幂函数
分析:由于上述不等式依托的函数是\\(y=x^{\\frac{1}{2}}\\),在定义域\\([0,+\\infty)\\)上单调递增,
故有\\(\\left\\{\\begin{array}{l}{2m+1\\ge 0①}\\\\{m^2+m-1\\ge 0②}\\\\{2m+1>m^2+m-1③}\\end{array}\\right.\\)
解得\\(\\left\\{\\begin{array}{l}{m\\ge -\\cfrac{1}{2}①}\\\\{m\\ge\\cfrac{\\sqrt{5}-1}{2}或m\\leq \\cfrac{-\\sqrt{5}-1}{2}②}\\\\{-1<m<2③}\\end{array}\\right.\\)
求交集得到,\\(\\cfrac{\\sqrt{5}-1}{2}\\leq m<2\\)。故\\(m\\in [\\cfrac{\\sqrt{5}-1}{2},2)\\)。
【变式1】【无奇偶性】若\\((2m+1)^{\\frac{1}{4}}>(m^2+m-1)^{\\frac{1}{4}}\\),求实数\\(m\\)的取值范围。
分析:求解过程同上,故\\(m\\in [\\cfrac{\\sqrt{5}-1}{2},2)\\)。
【变式2】【无奇偶性】若\\((2m+1)^{\\frac{1}{2n}}>(m^2+m-1)^{\\frac{1}{2n}}(n\\in N^{*})\\),求实数\\(m\\)的取值范围。
分析:求解过程同上,故\\(m\\in [\\cfrac{\\sqrt{5}-1}{2},2)\\)。
【变式3】【抽象函数】若函数\\(f(x)\\)的定义域为\\([0,+\\infty)\\),且满足对任意的\\(x_1,x_2\\in [0,+\\infty)\\),都有\\(\\cfrac{f(x_1)-f(x_2)}{x_1-x_2}>0(x_1\\neq x_2)\\),且满足\\(f(2m+1)>f(m^2+m-1)\\),求实数\\(m\\)的取值范围。
分析:求解过程同上,故\\(m\\in [\\cfrac{\\sqrt{5}-1}{2},2)\\)。
恒成立问题
【变式】\\(\\forall x\\in [1,5]\\),都能使得函数\\(f(x)=x^2 +ax-2\\ge 0\\)成立,求参数\\(a\\)的取值范围。
【常规】法1:二次函数法,由于\\(\\Delta=a^2+8>0\\),故不需要考虑\\(\\Delta<0\\)的情形,
只需要考虑对称轴\\(x=-\\cfrac{a}{2}\\)和给定区间\\([1,5]\\)的相对位置关系
当\\(-\\cfrac{a}{2}\\leq 1\\)时,即\\(a\\geqslant -2\\)时,函数\\(f(x)\\)在区间\\([1,5]\\)单调递增,
所以\\(f(x)_{min}=f(1)=1+a-2\\geqslant 0\\),解得\\(a\\geqslant 1\\),又因为\\(a\\geqslant -2\\),所以得到\\(a\\geqslant 1\\)。
当\\(-\\cfrac{a}{2}\\ge 5\\)时,即\\(a\\leqslant -10\\) 时,函数\\(f(x)\\)在区间 \\([1,5]\\)单调递减,
所以\\(f(x)_{min}=f(5)=25+5a-2\\ge 0\\),解得\\(a\\ge -\\cfrac{23}{5}\\),
又因为\\(a\\leq -10\\),所以得到\\(a\\in\\varnothing\\)。
当\\(1<-\\cfrac{a}{2}<5\\),即\\(-10<a<-2\\)时,\\(f(x)min=f(-\\cfrac{a}{2})=\\cfrac{a^2}{4}-\\cfrac{a^2}{2}-2≥0\\),
得到\\(a\\in\\varnothing\\)。(这种情形可以省略)
综上可得\\(a\\geqslant 1。\\)即\\(a\\)的取值范围是\\([1,+\\infty)\\)
【通法】法2:【恒成立+分离参数法】两边同时除以参数\\(a\\)的系数\\(x\\)(由于\\(x\\in [1,5]\\),不等号方向不变),得到
\\(a\\geqslant \\cfrac{2}{x}-x\\)在区间 \\([1,5]\\)上恒成立, 转化为求新函数“\\(\\cfrac{2}{x}-x\\)”在\\([1,5]\\)上的最大值。
这时我们一般是定义新函数,令\\(g(x)=\\cfrac{2}{x}-x\\),
则利用函数单调性的结论,可以看到\\(g(x)=\\cfrac{2}{x}-x\\)在区间 \\([1,5]\\)上单调递减,
所以\\(g(x)_{max}=g(1)=1\\),所以\\(a\\geqslant 1\\),即\\(a\\)的取值范围是\\([1,+\\infty)\\)
集合关系
【变式1】给定命题\\(p:m+1\\leq x\\leq 1-2m\\),命题\\(q:-2\\leq x\\leq 7\\),已知\\(q\\)是\\(p\\)的充分不必要条件,求实数\\(m\\)的取值范围。
【变式2】给定命题\\(p:m+1\\leq x\\leq 1-2m\\),命题\\(q:-2\\leq x\\leq 7\\),已知\\(p\\)是\\(q\\)的必要不充分条件,求实数\\(m\\)的取值范围。
【变式3】给定命题\\(p:m+1\\leq x\\leq 1-2m\\),命题\\(q:-2\\leq x\\leq 7\\),已知\\(\\neg p\\)是\\(\\neg q\\)的充分不必要条件,求实数\\(m\\)的取值范围。
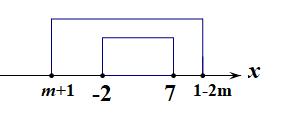
分析:自行画出草图可知,先列出条件\\(\\begin{cases}&m+1\\leq-2\\\\&1-2m \\ge 7\\end{cases}\\),解得\\(m\\leq -3\\),
接下来验证\\(m=-3\\)是否满足题意。
当\\(m=-3\\)时,\\(A=[-2,7]\\),\\(B=[m+1,1-2m]=[-2,7]\\),此时\\(A=B\\),不满足题意,舍去,
故实数\\(m\\)的取值范围为\\(\\{m\\mid m<-3\\}\\)。
解后反思:本题目如上处理,则可以避免分类讨论;
函数性质综合
分析:先求定义域,由于\\(\\sqrt{x^2+1}\\ge \\pm \\sqrt{x^2}\\),故定义域为\\((-\\infty,+\\infty)\\),
又由于\\(f(-x)=ln(\\sqrt{x^2+1}-x)\\),故\\(f(x)+f(-x)=ln1=0\\),故函数为奇函数。
当\\(x\\in [0,+\\infty)\\)时,\\(x^2\\nearrow\\),\\(1+x^2\\nearrow\\),\\(\\sqrt{1+x^2}\\nearrow\\),\\(x+\\sqrt{1+x^2}\\nearrow\\),
\\(y=ln(x+\\sqrt{1+x^2})\\nearrow\\),则由奇函数可知在\\((-\\infty,+\\infty)\\)上,\\(f(x)\\nearrow\\),
故由定义域为\\(R\\),奇函数,单调递增,则由\\(f(x-1)+f(x)>0\\),
得到\\(f(x-1)>-f(x)=f(-x)\\),即\\(x-1>-x\\),解得\\(x>\\cfrac{1}{2}\\),即\\(x\\in (\\cfrac{1}{2},+\\infty)\\)。
【变式1】已知奇函数\\(f(x)\\)定义域为\\(R\\),且单调递增,若\\(f(x-1)+f(x)>0\\),求\\(x\\)的取值范围;
【变式2】已知定义在\\(R\\)上的函数\\(f(x)\\)满足\\(f(-x)+f(x)=0\\),且在\\(x\\in [0,+\\infty)\\)上时,恒有\\(f\'(x)\\geqslant 0\\)成立,若\\(f(x-1)+f(x)>0\\),求\\(x\\)的取值范围;
【变式3】已知定义在\\(R\\)上的函数\\(f(x)\\)图像关于原点对称,且在\\(x_1,x_2\\in [0,+\\infty)\\)上时,有\\(\\cfrac{f(x_2)-f(x_1)}{x_2-x_1}>0(x_1\\neq x_2)\\)成立,若\\(f(x-1)+f(x)>0\\),求\\(x\\)的取值范围;
【变式1】已知不等式\\(x^2 +ax-2\\ge 0\\)在区间 \\([1,5]\\)上有解,求参数\\(a\\)的取值范围。
【变式2】已知不等式\\(x^2 +ax-2\\ge 0\\)在区间 \\([1,5]\\)上解集不是空集,求参数\\(a\\)的取值范围。
【变式3】已知不等式\\(x^2 +ax-2\\ge 0\\)在区间 \\([1,5]\\)上至少有一个解,求参数\\(a\\)的取值范围。
【变式4】已知命题\\(p\\):对任意\\(x\\in [1,5]\\),不等式\\(x^2+ax-2< 0\\)在区间 \\([1,5]\\)无实数解,是假命题,求参数\\(a\\)的取值范围。 ↩︎
 tags:
tags:  [思维发散拓展训练辅导]
[思维发散拓展训练辅导]