一题一世界—寻找解题的最短路径

Posted 2021-04-28 生长数学

一题多解是解题训练的重要方法，它不仅可以训练思维的开阔性和灵活性，而且可以寻找解题的最优方案，使解题更加高效，思维更加敏捷。

下面我们看一道2017年中考贵阳卷压轴填空题：

如图，在菱形纸片ABCD中 ，AB=2，∠A=60°，将菱形纸片翻折，使点 A 落在 CD 的中点 E 处，折痕为 FG ，点 F、G 分别在边 AB、AD 上，则 cos∠EFG的值为      .

小猿搜题的答案详解如下：

这个解答涉及了5个直角三角形的边长计算，看起来是不是有点繁琐臃肿？

我们想要更简洁更漂亮的思路。

图形的翻折可以说是初中数学常见常考的基本问题，我们有没有总结过这类问题中会出现的特殊图形？

看下图，易证一组边平行的四边形翻折后重叠部分一定是等腰三角形。

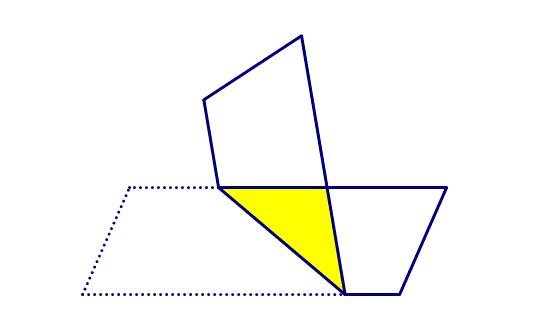
把重叠部分翻折就可以得到菱形：

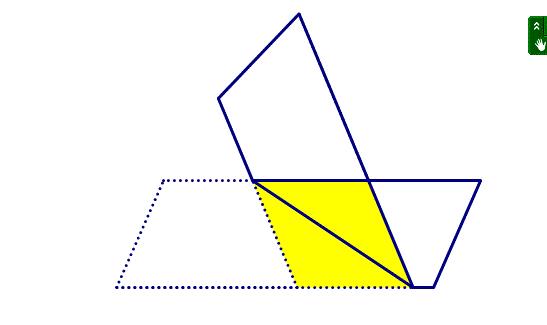
据此，我们在本题的图形中找到此等腰三角形或菱形就会发现问题简单多了。

这个方法直奔目标简洁明了，是如此的优美简约。

我们在平时解题过程中要进行深度思考，要在思考中有所发现，发现题目之间的联系，发现众多问题中的共同规律和本质。这样才能超越题海，拨开迷雾，达到左右逢源，一通百通的境界。