复合函数

Posted 2021-01-10 wanghai0666

一、什么是复合函数

• 基本初等函数：可以类比原子是构成物质的最基本的不可再分的微粒一样，来理解基本初等函数和其他函数的关系。

高中阶段所学习的函数中，只有

①常函数(f(x)=c(c为常数))、

②幂函数(f(x)=x^{alpha})、

③指数函数(f(x)=a^x(a>0且a eq 1))，

④对数函数(f(x)=log_ax(a>0且a eq 1))、

⑤三角函数(f(x)=sinx[或f(x)=cosx])等，五种基本初等函数，

以前的教材中还有一种⑥反三角函数(f(x)=arcsinx，xin[-cfrac{pi}{2}，cfrac{pi}{2}])等，现在不需要学生学习。

• 初等函数：由基本初等函数经过四则运算所构成的函数。

比如，一次函数(f(x)=kx+b(k eq 0))，其实是常函数(y=k)与幂函数(y=x)相乘，再与常函数(y=b)求和得到的。

比如，指数型函数(y=3cdot 2^x+1)，其实是常函数(y=3)与指数函数(y=2^x)相乘，再与常函数(y=1)求和得到的。

• 如果我们遇到的基本初等函数或初等函数的函数值再次充当了某个初等函数的自变量，这样形成的函数我们称之为复合函数。

• 复合函数：设函数(y=f(u))和(u=g(x))，则函数(y=f[g(x)])称为由(y=f(u))和(u=g(x))复合而成的复合函数，其中函数(y=f(u))常常称为外函数，函数(u=g(x))常常称为内函数，其中内函数的值域必须是外函数的定义域的子集。

• 定义域、值域、最值、单调性、周期性、奇偶性、对称性，

二、典例剖析：

(fbox{例1})【求复合函数的定义域】

已知函数(f(x))的定义域是([-1，1])，求函数(f(2x+1))的定义域；

分析：解决这类题目需要牢牢抓住两点：

其一接受对应法则(f)作用的(x)和(2x+1)是处于对等位置的，

其二不论是给定函数的定义域还是求解函数的定义域，

都是针对单独的自变量(x)而言，

据此可知由于(-1leq xleq 1)，故(-1leq 2x+1leq 1)，

解得函数(f(2x+1))的定义域是(xin [-1，0])。

(fbox{例2})【求复合函数的定义域】

已知函数(f(x+1))的定义域是([0，1])，求函数(f(2^x-2))的定义域。

分析：这里同样你得清楚(x+1)和(2^x-2)是对等的，

先由(xin[0，1])，计算得到(1leq x+1leq 2)，故(1leq 2^x-2leq 2)，

解得(3leq 2^xleq 4)，同时取以2为底的对数得到(log_2^3leq xleq 2)，

则所求定义域是(xin [log_2^3，2])。

(fbox{例3})【求复合函数的定义域】

已知函数(f(2x+1))的定义域是([-1，1])，求函数(f(x))的定义域；

分析：由上面的例子分析可知，所给函数的定义域是([-1，1])，

即函数(f(2x+1))的自变量(x)的取值范围是([-1，1])，

故内函数(2x+1)的取值范围这样求解，

由(-1leq x leq 1)，得到(-2leq 2x leq 2)，

所以(-1=-2+1leq 2x+1 leq 2+1=3)，

又由于(2x+1)和(x)对等(你可以理解为这两个接受同样的纪律约束也行)，

所以(f(x))的(x)的取值范围应该是(-1leq xleq 3)，

故函数(f(x))的定义域是([-1，3])。

(fbox{例4})【复合函数的单调性】

已知函数(f(x)=log_2(x^2-3x+2))，求其单调性。

分析：令(g(x)=x^2-3x+2)，由(g(x)=x^2-3x+2>0)，

解得(xin (-infty，1)cup(2，+infty))，

上述结果即为此复合函数的定义域。

即要研究其单调性，必须先在上述定义域范围内，定义域优先原则。

然后由(g(x)=x^2-3x+2=(x-cfrac{3}{2})^2-cfrac{1}{4})，

则内函数(g(x))在区间((2，+infty))上单调递增，在区间((-infty，1))上单调递减，

而外函数(y=f(t)=log_2t)只是单调递增的，

故复合函数(f(x))在区间((2，+infty))上单调递增，在区间((-infty，1))上单调递减。

(fbox{例2})(2017凤翔中学高三理科第二次月考第9题)
若函数(f(x)=log_a^;(6-ax))在([0，2])上为减函数，则实数(a)的取值范围是【】

A、([3，+infty)) (hspace{2cm}) B、((0，1)) (hspace{2cm}) C、((1，3]) (hspace{2cm}) D、 ((1，3))

分析：令(g(x)=6-ax)，像这类题目既要考虑单调性，还要考虑定义域。

由题目可知必有(a>0)，故函数(g(x))单调递减，考虑定义域时只要最小值(g(2)>0)即可，

再考虑外函数必须是增函数，故(a>1)，

结合(g(2)>0)，解得(1<a<3)，故选D。

(fbox{例3})【复合函数的求导】

①设(f(x)=sin(2x+1))，求导函数(f'(x))；

②设(g(x)=ln(x^2+3x))，求导函数(g'(x))；

分析：我们目前一般只涉及一次复合的函数如(y=f(u))和(u=g(x))，

则复合函数为(y=f[g(x)])，([f(g(x))]'=f'[g(x)]cdot g'(x))

①令(phi=2x+1)，则(y=f(x)=sinphi)，故(f'(x)=y'_x=y'_{phi}cdot phi'_x=cosphicdot 2=2cos(2x+1))；

②(g'(x)=cfrac{1}{x^2+3x}cdot (x^2+3x)'=cfrac{2x+3}{x^2+3x})；

说明：函数(f(x)=x^2pm lnx)，不是复合函数，只是两个函数(y=x^2)与函数(y=lnx)之间用四则运算构成的一个新函数。

(fbox{例4})【求复合函数的单调区间】【2018天津模拟】

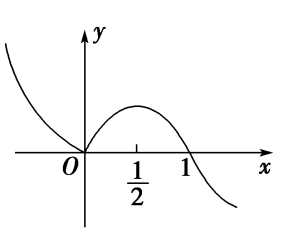
已知函数(y=f(x)(xin R))的图像如图所示，则函数(g(x)=f(log_ax)(0<a<1))的单调递减区间为【】

(A、[0，cfrac{1}{2}]) (hspace{4em}) (B、[sqrt{a}，1])

(C、(-infty，0)cup[cfrac{1}{2}，+infty)) (hspace{4em}) (D、[sqrt{a}，sqrt{a+1}])

分析：由图可知，外函数(f(x))在区间((-infty，0))和([cfrac{1}{2}，+infty))上单调递减，

在区间([0，cfrac{1}{2}])上单调递增，

又(0<a<1)时，内函数(y=log_ax)在区间((0，+infty))上单调递减，

故要使得复合函数函数(g(x)=f(log_ax)(0<a<1))单调递减，

则需要(log_axin [0，cfrac{1}{2}])，即(0leq log_axleq cfrac{1}{2})，

解得(xin [sqrt{a}，1])，故选B。