母函数及其应用+模板

Posted 2021-01-10 wkfvawl

部分摘自这位大佬的博客https://www.cnblogs.com/linyujun/p/5207730.html

生成函数即母函数，是组合数学中尤其是计数方面的一个重要理论和工具。 最早提出母函数的人是法国数学家LaplaceP.S.在其1812年出版的《概率的分析理论》中明确提出“生成函数的计算”。 生成函数的应用简单来说在于研究未知（通项）数列规律，用这种方法在给出递推式的情况下求出数列的通项。 

在这里我们不去高深地研究数学上母函数，而是讲讲简单的母函数应用。

1.母函数引入

就是把一个已知的序列和x的多项式合并起来，新产生的多项式就叫原来序列的母函数

序列{0,1，2，3，4，5...n}的母函数就是

f(x)=0+x+2x^2+3x^3+4x^4+...+nx^n（这个x没有任何意义，应该说，你不需要把它当做一个函数，你只要知道母函数这么写就可以了）

 

序列{1,1,1,1,1......}的母函数就是

f(x)=1+x+x^2+x^3+x^4....

 

二项式展开的序列比如这个{1,4,6,4,1,0,0,0,0,0.....}是C(4,0)到C(4,4)的系数，那它的母函数就是

f(x)=1+4x+6x^2+4x^3+1x^4

 

这些东西对于我们来说并没有说明意义，母函数对我们来说只是一个工具，是一个载体，那来看看母函数是怎么样装载数据的吧！

 

例1：若有1克、2克、3克、4克的砝码各一 枚，能称出哪几种重量？各有几种可能方案？ 

 假如x的指数表示砝码

那么

1克的砝码表示为1+x^1

2克的砝码表示为1+x^2

3克的砝码表示为1+x^3

4克的砝码表示为1+x^4

 

每个砝码都可以选择取或不取

所以这里的1可以认为1*x^0，表示不取这颗砝码

 那么把这些乘起来

(1+x^1)(1+x^2)(1+x^3)(1+x^4)

=1+(x^1)+(x^2)+2(x^3)+2(x^4)+2(x^5)+2(x^6)+2(x^7)+(x^8)+(x^9)+(x^10)

 

根据指数来看，我们可以称出0~10这么多的重量，其中3~7的系数为2，说明有2种称的方法

那么我们来细看一遍

0：（什么砝码都不放）.......................（1种）

1：1.............................................（1种）

2：2.............................................（1种）

3：3或1+2.....................................（2种）

4：4或1+3.....................................（2种）

5：1+4或2+3.................................（2种）

6：2+4或1+2+3..............................（2种）

7：3+4或1+2+4..............................（2种）

8：1+3+4......................................（1种）

9：2+3+4......................................（1种）

10：1+2+3+4.................................（1种）

 

分毫不差

所以说母函数在ACM就是这么用的，跟函数没关系，跟写法有关系。

 

例2：求用1分、2分、3分的邮票贴出不同数值的方案数，每种邮票可以有无限张。

因邮票允许重复，故母函数为：

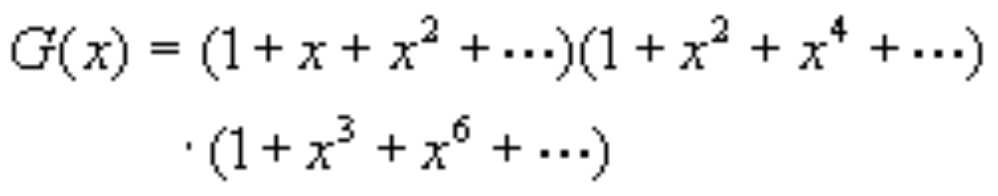
对于这种连续相乘，我们人类是很讨厌的，但对于计算机这种重复运算是很轻松的，我们只要将我们解多项式的思路带进去即可。

2.代码说明

我们首先知道对于最后得到的那一个母函数，系数代表的是方案数，而指数代表的是组成的数值，运算过程就是多项式的乘法。而两个多次方程的乘法，运算无非是系数相乘，指数相加，仅仅是这个方程的这么两个信息的运算。那能不能用什么数据结构直接表示出一个对象的这个两个信息呢？首先想到的可能是结构体，结构体可以用来表示一个对象的多个信息，但是运算繁琐；其实用数组就可以了，下标代表组成的数组，数值代表方案数！！！

a.求用1分、2分、3分的邮票贴出不同数值的方案数：（每张邮票的数量是无限的）

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 #define MAX 310
 6 int a[MAX];///最终合并的多项式
 7 int b[MAX];///临时合并用的多项式
 8 int n;
 9 const int N=110;
10 using namespace std;
11 void init()
12 {
13     int i,j,k;
14     a[0]=1;///一开始的0的情况
15     for (i=1; i<=3; i++)///代表1分,2分,3分三个多项式的合并
16     {
17         for (j=0; j<N; j+=i)///i分的邮票,步长为i
18         {
19             for (k=0; k+j<N; k++)///从x^0到x^N遍历一遍
20             {
21                 b[j+k]+=a[j];///核心
22             }
23         }
24         for (j=0; j<N; j++)///b中数据抄到a,b清空
25         {
26             a[j]=b[j];
27             b[j]=0;
28         }
29     }
30 }
31 int main()
32 {
33     int i,j,k;
34     init();
35     while(scanf("%d",&n)!=EOF)
36     {
37         printf("%d
",a[n]);
38     }
39     return 0;
40 }

 

b.hdu 1028

http://acm.hdu.edu.cn/showproblem.php?pid=1028

题目问一个数字n能够拆成多少种数字的和

比如n=4

  4 = 4;
  4 = 3 + 1;
  4 = 2 + 2;
  4 = 2 + 1 + 1;
  4 = 1 + 1 + 1 + 1;

有5种，那么答案就是5

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 #define MAX 130
 6 #define N 130
 7 #define ll long long int
 8 ll a[MAX];
 9 ll b[MAX];
10 int n;
11 using namespace std;
12 void init()
13 {
14     int i,j,k;
15     a[0]=1;
16     for (i=1; i<=MAX; i++)
17     {
18         for (j=0; j<N; j+=i)
19         {
20             for (k=0; k+j<N; k++)
21             {
22                 b[j+k]+=a[k];
23             }
24         }
25         for (j=0; j<N; j++)
26         {
27             a[j]=b[j];
28             b[j]=0;
29         }
30     }
31 }
32 int main()
33 {
34     init();
35     while(scanf("%d",&n)!=EOF)
36     {
37         printf("%lld
",a[n]);
38     }
39     return 0;
40 }

View Code

 

c.hdu 1398

http://acm.hdu.edu.cn/showproblem.php?pid=1398

题目说一个国家的硬币都是方形的，面值也是方形的

有1块钱，4块钱，9块钱，16块钱......一直到289块钱（17^2）

问想组成n块钱有几种方法

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 #define ll long long int
 6 #define MAX 17
 7 #define N 305
 8 using namespace std;
 9 ll a[N];
10 ll b[N];
11 void init()
12 {
13     int i,j,k;
14     a[0]=1;
15     for (i=1; i<=MAX; i++)
16     {
17         for (j=0; j<N; j+=i*i)
18         {
19             for (k=0; k+j<N; k++)
20             {
21                 b[j+k]+=a[k];
22             }
23         }
24         for (j=0; j<N; j++)
25         {
26             a[j]=b[j];
27             b[j]=0;
28         }
29     }
30 }
31 int main()
32 {
33     int n;
34     init();
35     while(scanf("%d",&n)!=EOF)
36     {
37         if(n==0)
38         {
39             break;
40         }
41         printf("%lld
",a[n]);
42     }
43     return 0;
44 }

View Code