赏月斋源码共享计划 第四期 约瑟夫问题

Posted sddai

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了赏月斋源码共享计划 第四期 约瑟夫问题相关的知识，希望对你有一定的参考价值。

约瑟夫问题求解及优化

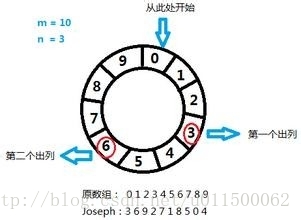
问题描述

在一间房间总共有n个人，给定一个数k，然后按照如下规则去杀人：

  1. 所有人围成一个圆圈，按顺时针依次给所有人编号：1, 2, 3…, n
  2. 由编号1开始报数，按顺时针方向，报到数字k的人将被杀掉
  3. 被杀掉的人从房间内被移走，从被杀的下一个人重新由1开始报数
  4. 报到数字k的人再次被杀掉，再移走，再次开始报数，一直杀到最后剩余一个人

最后剩余的人活命。

那么，给定了 n 和 k，最后活下来的人的编号是几？

思路一

根据问题描述，可以使用循环单链表模拟杀人过程：

  1. 表头是1号，表尾是n号，循环单链表的表尾指向表头模拟圆圈
  2. 指针从表头1号开始走，当指到第k个节点时，即当报k的被杀时，就将该节点从链表中删除。
  3. 删除该节点后，从该节点的下一个节点开始，再从1走到k,
  4. 再次删除第k节点，一直到某节点的下一个节点指向自己，说明只有一个节点了，即最后活下的人

根据上面分析循环单链表的操作过程，代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Node(object):
def __init__(self, value):
self.value = value
self.next = None
 
def create_linkList(people_num):
"""创新循环单链表"""
head = Node(1)
pre = head
for i in range(2, people_num+1):
newNode = Node(i)
pre.next = newNode
pre = newNode
pre.next = head
return head
 
people_num = 5 # 总人数
k = 2 #报k被杀
 
if k == 1:
print("最后存活编号：" + str(people_num))
else:
head = create_linkList(people_num)
pre = None
cur = head # 当前报数的人
while cur.next != cur: # #终止条件是节点的下一个节点指向本身,即只剩一个节点
for i in range(k-1):
# 走到第k节点
pre = cur
cur = cur.next
print("杀掉：" + str(cur.value)) # 被删除节点编号
# 删除节点
pre.next = cur.next
# 从被删除节点的下一个节点从新报数
cur.next = None
cur = pre.next
print("最后存活者编号是:" + str(cur.value))

这种方法的时间复杂度为：O(n*k),当人数量n很大，报的数k也很大时，并不适用。

思路二

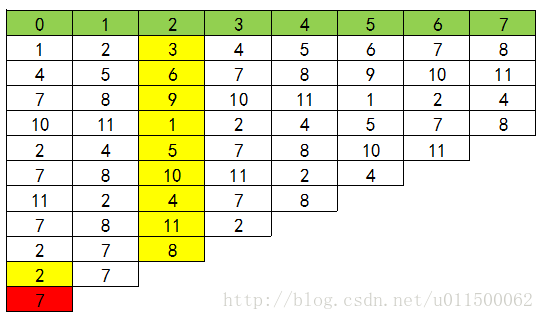
递归思路，假设房间共有n = 10个人，初始编号为1,2,3,…10，设初始编号对应的编号位置为0, 1, 2, …9, 每次数到k = 3的人杀死，求最后活下来的人的初始编号是几？

来看杀人过程：

技术分享图片约瑟夫问题递归思路求解过程

(表中红色为报数k=3的被杀死的人的编号，绿色为最后活下来的人的编号)

仔细观察表中每一轮初始编号的移动规律：

第二轮到第一轮的编号移动规律： (第二轮的编号x的编号位置 + k) % 10 ==> 第一轮编号x的编号位置
比如第二轮编号5的编号位置是1， (1 + 3) % 10 ==> 4, 得到第一轮编号5的的编号位置是4

进而得到第三轮到第二轮的编号移动规律：(第三轮编号x的编号位置 + k) % 9 ==> 第二轮编号x的编号位置
比如第三轮编号5的编号位置是7， (7 + 3) % 9 –> 1, 得到第二轮编号5的的编号位置是1

进而得到第N轮与第N-1轮的编号移动规律：(第N轮的编号x的编号位置 + k) % 第N-1轮总人数 ==> 第N-1轮编号x的编号位置

最后一轮存活着的编号x对应的编号位置一定是0， 那么根据以上规律，可以得到倒数第二轮编号x对应的编号位置，根据规律进一步可以得到倒数第三轮编号x对应的编号位置， 一直可以推导出第一轮编号x的对应编号位置，由第一轮编号x的对应编号位置+1得到的便是最后存活的人的初始编号。

由上总结，当房间共有n个人，报数k杀死时，令f(n, k)表示最后存活着的编号位置，则有递归公式：

  • n = 1: f(1, k) = 0;
  • n > 1: f(n, k) = (f(n-1, k) + k) % n;

有了递推公式以后，代码实现如下：

1
2
3
4
5
6
7
8
9
def josephus(n, k):
if n == 1:
return 0
else:
return (josephus(n - 1, k) + k) % n
 
n = 10
k = 3
print("最后存活者编号是：", josephus(n, k)+1) # 4

对思路二的优化

对递归思路的进一步优化，假设n非常大，而k又比较小，比如n=100, k=3, 被杀过程如下：

  • 第一轮： 有100个人，每次报k=3的被杀，总共杀死了 math.floor(100/3) = 33个人，剩余67个人
  • 第二轮： 有67个人，每次报k=3的被杀，总共杀死了 math.floor(67/3) = 22个人，剩余45个人
  • 第三轮： 有45个人，每次报k=3的被杀，总共杀死了 math.floor(45/3) = 15个人，剩余30个人
  • 第四轮： 有30个人，每次报k=3的被杀，总共杀死了 math.floor(30/3) = 10个人，剩余20个人
  • 第五轮： 有20个人，每次报k=3的被杀，总共杀死了 math.floor(20/3) = 6个人，剩余14个人
  • 第六轮： 有14个人，每次报k=3的被杀，总共杀死了 math.floor(14/3) = 4个人，剩余10个人
  • 第七轮： 有10个人，每次报k=3的被杀，总共杀死了 math.floor(10/3) = 3个人，剩余7个人
  • 第八轮： 有7个人，每次报k=3的被杀，总共杀死了 math.floor(7/3) = 2个人，剩余5个人
  • 第九轮： 有5个人，每次报k=3的被杀，总共杀死了 math.floor(5/3) = 1个人，剩余4个人
  • 第十轮： 此时，总人数n=4, 报的数k=3，再利用思路二中的递归方法求解最后剩余者编号

在上面杀人过程中，通过建立n/k的步长加快了杀人的速度，减少了算法时间。可以从下面这幅图中更加清晰的体会到：

技术分享图片约瑟夫问题递归思路求解过程优化

本来需要10轮的，现在只需要7轮，如果n=100，k=3的话优化效果会更明显。

根据以上分析，优化方法如下：

  • math.floor(n/k) == 1: 用思路二中方法求解
  • math.floor(n/k) > 1: n = n - math.floor(n/k)

实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import math
def josephus(n, k):
if n == 1:
return 0
else:
return (josephus(n - 1, k) + k) % n
 
def kill_people(n, k):
while math.floor(n/k) > 1:
# 建立一个步长为n/k的递归过程；
n = n - math.floor(n/k)
kill_people(n, k)
 
live_index = josephus(n, k)
return live_index+1
 
n = 10
k = 3
 
print("最后存活者编号是", kill_people(n,k))

思路三

使用数组存储房间中的每个人: arr = [ i for i in range(1, 10+1) ]
arr数组代表房间里的10个人：[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
每次被杀的人的编号： kill_num = (kill_num + k - 1) % len(arr)。 其中的(k-1)对应数组的下标
有了被杀人的的编号后，将其pop出数组。
然后再次计算下一个被杀人的编号，直到数组中只剩一个人。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
def josephus(n, k):
arr = [ i for i in range(1, n+1) ]
kill_num = 0
while len(arr) != 1:
kill_num = (kill_num + k - 1) % len(arr)
print("杀死：" + str(arr.pop(kill_num)))
return arr[0]
 
 
n = 10
k = 3
print("最后存活者编号是：", josephus(n, k)) # 4

对思路三的优化

在思路三中需要构建一个数组，也可以不用数组来减少内存。使用动态规划来解：

1
2
3
4
5
6
7
8
9
def Josephus(n, k):
kill_num = 0
for i in range(1, n+1):
kill_num = (k + kill_num) % i
return kill_num + 1
 
n = 5
k = 2
print("最后存活者编号：", Josephus(n, k))

最后这个动态规划的方法来自：https://www.quora.com/What-is-the-best-solution-for-Josephus-problem-algorithm

 

约瑟夫问题

约瑟夫问题是个著名的问题：N个人围成一圈，第一个人从1开始报数，报M的将被杀掉，下一个人接着从1开始报。如此反复，最后剩下一个，求最后的胜利者。
例如只有三个人，把他们叫做A、B、C，他们围成一圈，从A开始报数，假设报2的人被杀掉。

  • 首先A开始报数，他报1。侥幸逃过一劫。
  • 然后轮到B报数，他报2。非常惨，他被杀了
  • C接着从1开始报数
  • 接着轮到A报数，他报2。也被杀死了。
  • 最终胜利者是C

解决方案

普通解法

刚学数据结构的时候，我们可能用链表的方法去模拟这个过程，N个人看作是N个链表节点，节点1指向节点2，节点2指向节点3，……，节点N-1指向节点N，节点N指向节点1，这样就形成了一个环。然后从节点1开始1、2、3……往下报数，每报到M，就把那个节点从环上删除。下一个节点接着从1开始报数。最终链表仅剩一个节点。它就是最终的胜利者。
技术分享图片

缺点：

要模拟整个游戏过程，时间复杂度高达O(nm)，当n，m非常大(例如上百万，上千万)的时候，几乎是没有办法在短时间内出结果的。

公式法

约瑟夫环是一个经典的数学问题，我们不难发现这样的依次报数，似乎有规律可循。为了方便导出递推式，我们重新定义一下题目。
问题： N个人编号为1，2，……，N，依次报数，每报到M时，杀掉那个人，求最后胜利者的编号。

这边我们先把结论抛出了。之后带领大家一步一步的理解这个公式是什么来的。
递推公式：

 
f(N,M)=(f(N−1,M)+M)%Nf(N,M)=(f(N−1,M)+M)%N

 

  • f(N,M)f(N,M)表示，N个人报数，每报到M时杀掉那个人，最终胜利者的编号
  • f(N−1,M)f(N−1,M)表示，N-1个人报数，每报到M时杀掉那个人，最终胜利者的编号

下面我们不用字母表示每一个人，而用数字。

 
1、2、3、4、5、6、7、8、9、10、111、2、3、4、5、6、7、8、9、10、11

表示11个人，他们先排成一排，假设每报到3的人被杀掉。

 

  • 刚开始时，头一个人编号是1，从他开始报数，第一轮被杀掉的是编号3的人。
  • 编号4的人从1开始重新报数，这时候我们可以认为编号4这个人是队伍的头。第二轮被杀掉的是编号6的人。
  • 编号7的人开始重新报数，这时候我们可以认为编号7这个人是队伍的头。第三轮被杀掉的是编号9的人。
  • ……
  • 第九轮时，编号2的人开始重新报数，这时候我们可以认为编号2这个人是队伍的头。这轮被杀掉的是编号8的人。
  • 下一个人还是编号为2的人，他从1开始报数，不幸的是他在这轮被杀掉了。
  • 最后的胜利者是编号为7的人。

下图表示这一过程（先忽视绿色的一行）
技术分享图片

现在再来看我们递推公式是怎么得到的！
将上面表格的每一行看成数组，这个公式描述的是：幸存者在这一轮的下标位置

  • f(1,3)f(1,3)：只有1个人了，那个人就是获胜者，他的下标位置是0
  • f(2,3)=(f(1,3)+3)%2=3%2=1f(2,3)=(f(1,3)+3)%2=3%2=1：在有2个人的时候，胜利者的下标位置为1
  • f(3,3)=(f(2,3)+3)%3=4%3=1f(3,3)=(f(2,3)+3)%3=4%3=1：在有3个人的时候，胜利者的下标位置为1
  • f(4,3)=(f(3,3)+3)%4=4%4=0f(4,3)=(f(3,3)+3)%4=4%4=0：在有4个人的时候，胜利者的下标位置为0
  • ……
  • f(11,3)=6f(11,3)=6

很神奇吧！现在你还怀疑这个公式的正确性吗？上面这个例子验证了这个递推公式的确可以计算出胜利者的下标，下面将讲解怎么推导这个公式。
问题1：假设我们已经知道11个人时，胜利者的下标位置为6。那下一轮10个人时，胜利者的下标位置为多少？
答：其实吧，第一轮删掉编号为3的人后，之后的人都往前面移动了3位，胜利这也往前移动了3位，所以他的下标位置由6变成3。

问题2：假设我们已经知道10个人时，胜利者的下标位置为3。那下一轮11个人时，胜利者的下标位置为多少？
答：这可以看错是上一个问题的逆过程，大家都往后移动3位，所以f(11,3)=f(10,3)+3f(11,3)=f(10,3)+3。不过有可能数组会越界，所以最后模上当前人数的个数，f(11,3)=（f(10,3)+3）%11f(11,3)=（f(10,3)+3）%11

问题3：现在改为人数改为N，报到M时，把那个人杀掉，那么数组是怎么移动的？
答：每杀掉一个人，下一个人成为头，相当于把数组向前移动M位。若已知N-1个人时，胜利者的下标位置位f(N−1,M)f(N−1,M)，则N个人的时候，就是往后移动M为，(因为有可能数组越界，超过的部分会被接到头上，所以还要模N)，既f(N,M)=(f(N−1,M)+M)%nf(N,M)=(f(N−1,M)+M)%n

注：理解这个递推式的核心在于关注胜利者的下标位置是怎么变的。每杀掉一个人，其实就是把这个数组向前移动了M位。然后逆过来，就可以得到这个递推式。

因为求出的结果是数组中的下标，最终的编号还要加1

下面给出代码实现：

int cir(int n,int m)
{
    int p=0;
    for(int i=2;i<=n;i++)
    {
        p=(p+m)%i;
    }
    return p+1;
}
--------------------- 本文来自 陈浅墨 的CSDN 博客 ，全文地址请点击：https://blog.csdn.net/u011500062/article/details/72855826?utm_source=copy 

以上是关于赏月斋源码共享计划 第四期 约瑟夫问题的主要内容，如果未能解决你的问题，请参考以下文章

赏月斋源码共享计划 第七期 括号匹配

赏月斋源码共享计划 第三期

UNIZEN每周洞察第四期：Unizen生态迎来丰富进展

第四期“一生一芯”来了，欢迎报名

第四期“一生一芯”来了，欢迎报名

自动驾驶第四弹||自动驾驶的未来，共享or私人拥有？