BitMap算法详解

Posted 2020-10-15

　　所谓的BitMap就是用一个bit位来标记某个元素所对应的value，而key即是该元素，由于BitMap使用了bit位来存储数据，因此可以大大节省存储空间。

基本思想：

　　这此我用一个简单的例子来详细介绍BitMap算法的原理。假设我们要对0-7内的5个元素(4,7,2,5,3)进行排序(这里假设元素没有重复)。我们可以使用BitMap算法达到排序目的。要表示8个数，我们需要8个byte。

　　1.首先我们开辟一个字节(8byte)的空间，将这些空间的所有的byte位都设置为0

　　2.然后便利这5个元素，第一个元素是4，因为下边从0开始，因此我们把第五个字节的值设置为1

　　3.然后再处理剩下的四个元素，最终8个字节的状态如下图

　　

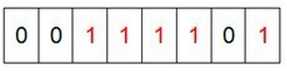
　　4.现在我们遍历一次bytes区域，把值为1的byte的位置输出(2,3,4,5,7)，这样便达到了排序的目的

　　从上面的例子我们可以看出，BitMap算法的思想还是比较简单的，关键的问题是如何确定10进制的数到2进制的映射图

MAP映射：

　　假设需要排序或则查找的数的总数N=100000000，BitMap中1bit代表一个数字，1个int = 4Bytes = 4*8bit = 32 bit,那么N个数需要N/32 int空间。所以我们需要申请内存空间的大小为int a[1 + N/32]，其中：a[0]在内存中占32为可以对应十进制数0-31，依次类推：

　　a[0]-----------------------------> 0-31

　　a[1]------------------------------> 32-63

　　a[2]-------------------------------> 64-95

　　a[3]--------------------------------> 96-127

　　......................................................

　　那么十进制数如何转换为对应的bit位，下面介绍用位移将十进制数转换为对应的bit位:

　　1.求十进制数在对应数组a中的下标

　　十进制数0-31，对应在数组a[0]中，32-63对应在数组a[1]中，64-95对应在数组a[2]中………，使用数学归纳分析得出结论：对于一个十进制数n，其在数组a中的下标为：a[n/32]

　　2.求出十进制数在对应数a[i]中的下标

　　例如十进制数1在a[0]的下标为1，十进制数31在a[0]中下标为31，十进制数32在a[1]中下标为0。 在十进制0-31就对应0-31，而32-63则对应也是0-31，即给定一个数n可以通过模32求得在对应数组a[i]中的下标。

　　3.位移

　　对于一个十进制数n,对应在数组a[n/32][n%32]中，但数组a毕竟不是一个二维数组，我们通过移位操作实现置1

　　a[n/32] |= 1 << n % 32
　　移位操作：
　　a[n>>5] |= 1 << (n & 0x1F)

　　n & 0x1F 保留n的后五位 相当于 n % 32 求十进制数在数组a[i]中的下标

代码实现：

　　

public class BitMap {

    private static final int N = 10000000;

    private int[] a = new int[N/32 + 1];

    /**
     * 设置所在的bit位为1
     * @param n
     */
    public void addValue(int n){
        //row = n / 32 求十进制数在数组a中的下标
        int row = n >> 5;
        //相当于 n % 32 求十进制数在数组a[i]中的下标
        a[row] |= 1 << (n & 0x1F);
    }

    // 判断所在的bit为是否为1
    public boolean exits(int n){
        int row = n >> 5;
        return (a[row] & ( 1 << (n & 0x1F))) != 1;
    }

    public void display(int row){
        System.out.println("BitMap位图展示");
        for(int i=0;i<row;i++){
            List<Integer> list = new ArrayList<Integer>();
            int temp = a[i];
            for(int j=0;j<32;j++){
                list.add(temp & 1);
                temp >>= 1;
            }
            System.out.println("a["+i+"]" + list);
        }
    }

    public static void main(String[] args){
        int num[] = {1,5,30,32,64,56,159,120,21,17,35,45};
        BitMap map = new BitMap();
        for(int i=0;i<num.length;i++){
            map.addValue(num[i]);
        }

        int temp = 120;
        if(map.exits(temp)){
            System.out.println("temp:" + temp + "has already exists");
        }
        map.display(5);
    }
}

运行结果如下：

temp:120has already exists
BitMap位图展示
a[0][0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
a[1][1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
a[2][1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
a[3][0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
a[4][0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]

应用范围：
　　可以运用在快速查找、去重、排序、压缩数据等。