分块+莫队

Posted 2021-01-08 cloud-king

分块：

分段预处理答案，在询问时，满足一整个块的，块间暴力；不满足完整一个区域的，块内直接暴力；

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cmath>
//提交SE;
using namespace std;
const int maxn=1e5+10;
typedef long long ll;

int belong[maxn],l[maxn],r[maxn],num,block,n;
ll a[maxn],val[maxn];

void buid()
{
    block=sqrt(n);                      //块的大小
    num=n/block;if(n%block)num++;       //块的数量；
    for(int i=1;i<=num;i++)
        l[i]=(i-1)*block+1,r[i]=block*i;//每块的左右端点值
    r[num]=n;
    for(int i=1;i<=n;i++)
        belong[i]=(i-1)/block+1;        //每块i属于哪一块;
    //更新块内信息;
    for(int i=1;i<=num;i++)
    {
        for(int j=l[i];j<=r[i];j++)
            val[i]=max(val[i],a[j]);//块内最大值;
    }
}
void updata(int x,int y)
{
    a[x]+=y;
    val[belong[x]]=max(val[belong[x]],a[x]);
}
ll ask(int x,int y)
{
    ll ans=0;
    if(belong[x]==belong[y])//块内暴力
    {
        for(int i=x;i<=y;i++)
            ans=max(a[i],ans);
        return ans;
    }
    for(int i=x;i<=r[belong[x]];i++)//首端块内暴力;
        ans=max(a[i],ans);
    for(int i=belong[x]+1;i<belong[y];i++)//块间暴力;
        ans=max(val[i],ans);
    for(int i=l[belong[y]];i<=y;i++)//尾端块内暴力;
        ans=max(ans,a[i]);
    return ans;
}
int main()
{
    int q;
    scanf("%d%d",&n,&q);
    buid();
    while(q--){
        int op,p,x;
        scanf("%d%d%d",&op,&p,&x);
        if(op==1){
            updata(p,x);
        }else{
            printf("%lld
",ask(p,x));
        }
    }
    return 0;
}

莫队：

将询问存储，经过一定的方式排序，减少冗余查询的算法。

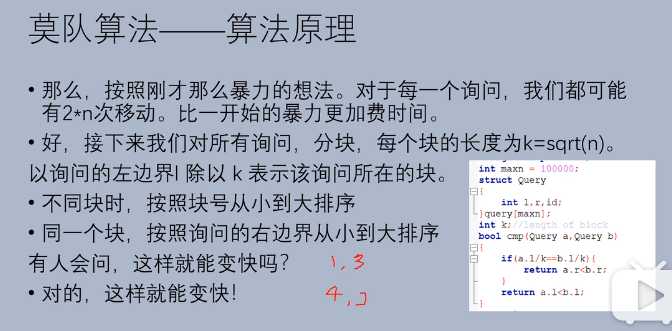
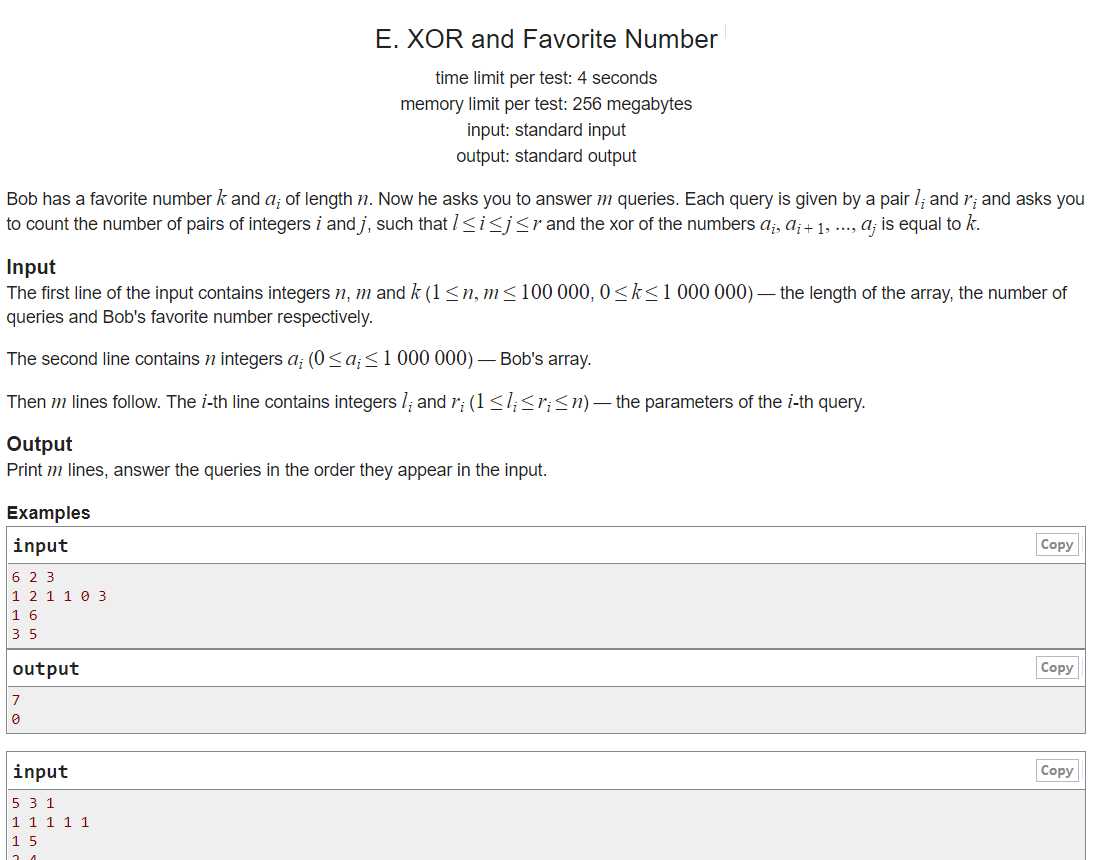
例：http://codeforces.com/contest/617/problem/E

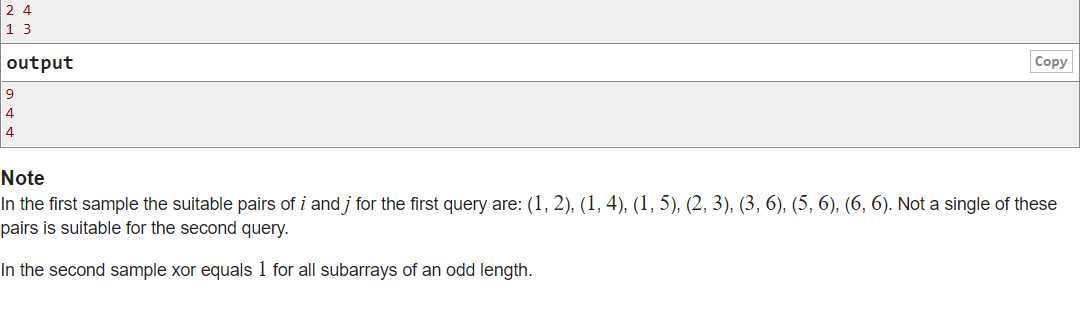
题目大意：求给定l和r之间，连续的异或和为k的对数;

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn=1<<20;           //这里是坑;
typedef long long ll;

struct node{                    //询问区间
    int l,r,id;
}Q[maxn];

int n,m,k;
int a[maxn],pos[maxn];          //存数列异或的前缀和，每个数在哪个块
ll flag[maxn],ans[maxn];

int L=1,R=0;
ll res=0;                       //初始区间
bool cmp(node x,node y)         //将询问区间排序
{
    if(pos[x.l]==pos[y.l])      //同一个块，按照询问的右边界从小到大排序；
        return x.r<y.r;
    return pos[x.l]<pos[y.l];   //不同块时，按照询问的右边界从小到大排序；
}
void add(int x)
{
    res+=flag[a[x]^k];
    flag[a[x]]++;
}
void del(int x)
{
    flag[a[x]]--;
    res-=flag[a[x]^k];
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    int sz=sqrt(n);             //分块;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        a[i]=a[i]^a[i-1];       //异或的前缀和;
        pos[i]=i/sz;            //每个i在哪个块里;
    }
    for(int i=1;i<=m;i++)       //输入询问
    {
        scanf("%d%d",&Q[i].l,&Q[i].r);
        Q[i].id=i;
    }
    sort(Q+1,Q+1+m,cmp);
    flag[0]=1;
    for(int i=1;i<=m;i++)
    {
        while(L<Q[i].l){        //将L加到l
            del(L-1);
            L++;
        }
        while(L>Q[i].l){
            L--;
            add(L-1);
        }
        while(R<Q[i].r)         //将R加到r
        {
            R++;
            add(R);
        }
        while(R>Q[i].r){        //将R减到r
            del(R);
            R--;
        }
        ans[Q[i].id]=res;

    }
    for(int i=1;i<=m;i++)
    {
        cout << ans[i] << endl;
    }
    return 0;
}