20172306 2018-2019 《Java程序设计与数据结构》第一周学习总结

Posted 2021-01-05 lc1021

20172306 2018-2019 《Java程序设计与数据结构（下）》第一周学习总结

教材学习内容总结

第一章 概述

（程序=数据结构+算法 软件=程序+软件工程）

• 1.1 软件质量
  • 软件工程师一门关于高质量软件开发的技术和理论的学科
  • 软件工程的目标：1.解决正确性问题 2.按时且在预算之内给出解决方案 3.给出高质量的解决方案 4.以合情合理的方式完成上面的事情
  • 高质量软件的特征
    
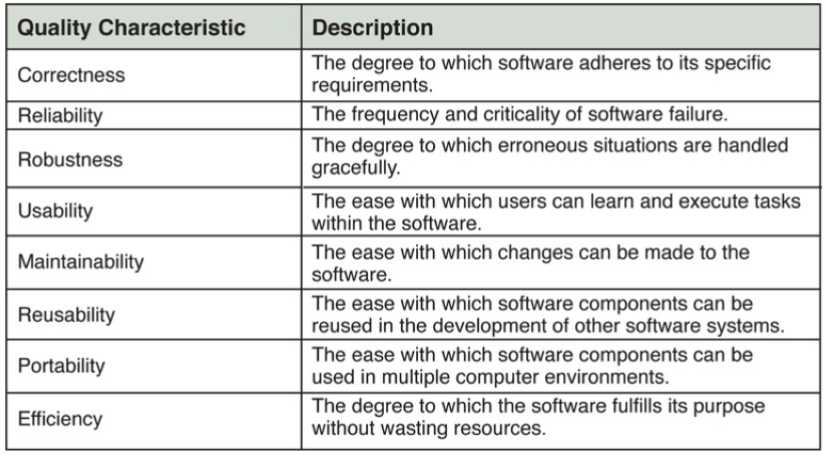
• 正确性：我认为是我们所做的都是为了解决一个正确性问题。
• 可靠性：降低软件的故障程度和概率
• 健壮性：可以很好地解决出现异常的情况
• 可用性：保证该软件可以很好地使用
• 可维护性：对于软件，是一个长期使用和改进的过程，因此，一个好的软件需要有维护性，可以持续的维护和发展
• 可重用性：我认为是创造的软件可以用在另一种软件上，提高了效率也提高了利用率
• 可移植性：就是一款软件可以在很多不同的环境中同样适用

• 运行效率：一个好的软件的运行效率也是条件之一。

• 1.2 数据结构
  • 软件开发的目的是构建软件，而不仅仅是编写代码。
  • 栈可用于颠倒数据集的顺序；队列可以保持其数据的顺序
• 自测题
  • 可靠性关注的是发生故障的频率和环境；健壮性关注的是出现故障会发生什么
  • 结构良好、设计良好以及文档说明良好的软件更容易维护

第二章 算法分析

（算法分析是计算机科学的基础）

• 2.1 算法效率分析
  • 为完成某一特定任务所使用的算法的效率，是决定一个程序运行速度的主要因素
• 2.2 增大函数与大O记法
  • 增长函数表示了该算法的时间复杂度或空间复杂度
  • 我们主要讨论算法的渐进复杂度，渐进复杂度称为算法的阶次（忽略该算法的增长函数中的常量和其他次要项，只保留主项而得出的）
    
  • 算法的阶次为增长函数提供了一个上界
  • 所有具有相同阶次的算法，从运行效率的角度来说都认为是等价的
• 2.3 增长函数的比较
  
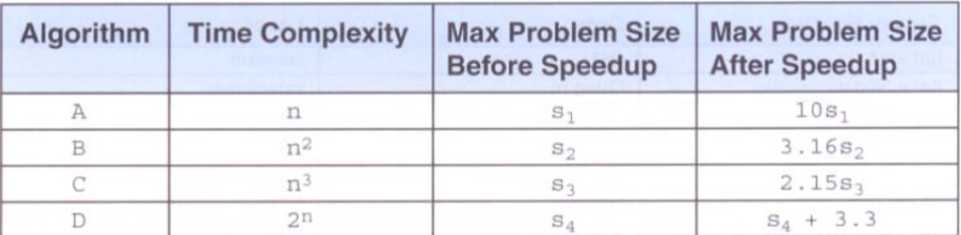
  • 寻求一个更高效的算法是一种比使用更快处理器的更好解决方法
  • 增长函数的比较
    
    
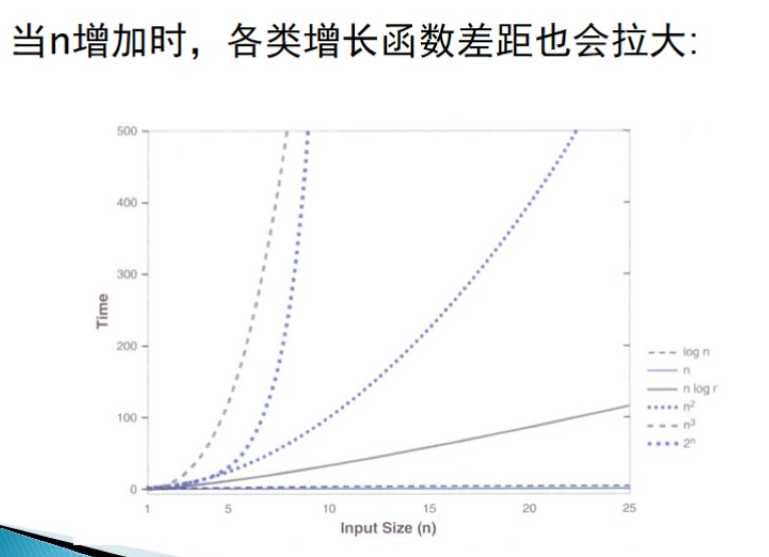
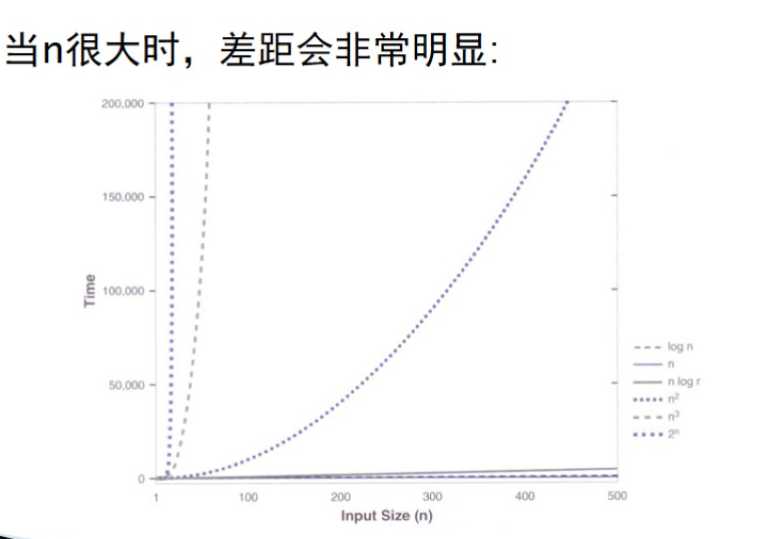
• 2.4 时间复杂度分析
  • 1.循环运行复杂度
  • （1）循环体复杂为O（1），需要循环n次，则时间复杂度为O(n).

  for(int count = 0;count<n;count++)
    {
    //*复杂度为O(1)的步骤系列
      }

  • （2）其实我自己认为这种情况时，一般我会动手计算一下，虽然速度慢，但是却可以更好的理解。则时间复杂度为O（logn）.

  count = 1;
   while(count < n)
   {
   count *=2;
   //复杂度为O(1)的步骤系列
   }

  • 2.嵌套循环复杂度
  • 对于循环体中的复杂度也需要考虑时，要将内层和外层都考虑好。该复杂度为O（n2）。

  • for(int count = 0;count < n;count++)
    {
    for(int count2 = 0;count2<n;count2++)
     {
         //复杂度为O(1)的步骤系列
     }
    }

  • 3.方法调用复杂度

  • 自己总结一下就是：我们在循环体中可能会引用一个方法，这个方法的复杂度是不确定的，但是同样的目的，它的复杂度是可能不同，所以具体还是要根据方法体的复杂度。

• 自测题
  • 随着问题的增大，算法的复杂度将不断接近该渐进复杂度
  • 随着算法复杂度的增长，处理器素的的提高对复杂度的影响越来越小

教材布置问题解答

• EX2.1 下列增长函数的阶次是多少？
• a.10n^2+100n+1000
  解：阶次就是渐进复杂度，对于该三项来说，第一项增长速度最快，主项是n^2，所以阶次就是n^2.
• b.10n^3-7
  解： 10n^3的增长速度最快，因此阶次为n^3
• c. 2^n+100n^3
  解：就这两项而言，我们可以看前面的增长函数的比较，可以发现n^3增长速度快，所以阶次为n^3.

• d. n^2logn
  解：阶次为n^2logn.

• EX2.4请确定下面代码段的增长函数和阶次

for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
        {
            System.out.println(count,count2);
        }
}

解：增长函数是n^2/2;阶次是n^2. 因为先看里面的，会发现内循环要进行n/2次，外循环要进行n次，根据之前学的，将内外相乘，则为n^2/2。

• EX2.5请确定下面代码段的增长函数和阶次

for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 * 2)
        {
            System.out.println(count,count2);
        }
}

解：增长函数是nlogn,阶次为nlogn. 因为，可以先列出几个，会发现内层循环次数为logn，而外层是n次，内外相乘为nlogn .

结对及互评

点评模板：

• 博客中值得学习的或问题：
  • xxx
  • xxx

点评过的同学博客和代码

• 本周结对学习情况
  • 20172325
  • 结对学习内容
    • 一起看了第一二章的内容
    • 一起完成的课后布置的习题

其他（感悟、思考等，可选）

 新学期开始了，又要和Java这门课斗智斗勇了！上学期这门课学的不咋地，这学期不知道能够学成什么样。假期说起博客的事情，我说我不爱写博客，我爸说，你都看书了为什么你就不好好把博客写的好点呢？我一想，有点道理，所以呢，刚开学，还是要对自己有信心的，争取这学期能保持好好写博客，学好这门课！！！

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0/0	1/1	6/6

参考资料

• Java结构设计与数据结构(第四版)