二叉搜索树的前驱和后继详细推导

Posted 2021-01-05 jasontodd

后继和前驱

定义：一个结点的后继，是大于x.key的最小关键字的结点。

           一个结点的前驱，是小于x.key的最大关键字的结点。

思路：找一个结点的前驱或者后继，无非是在三个区域找。

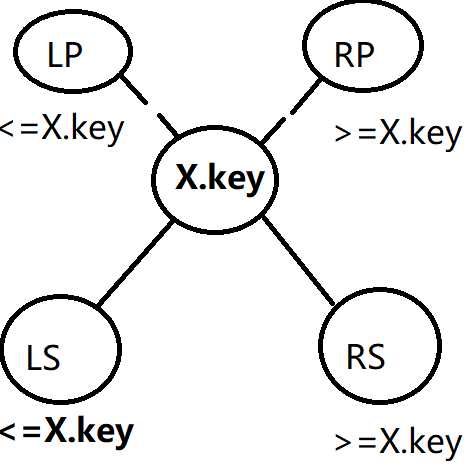
首先分析前驱：

满足两个条件，一是要小于当前键值，那么只有LP和LS区可以找。

                    二要求是其中最大的值。我们知道，对于LP来说，X、LS、RS都属于他的右子树，那么，X、LS和RS都是大于它的。

所以很显然，前驱就是LS中的最大值，即前驱 = 左子树中的最大值。条件是：存在左子树。

那不存在左子树只有左父母的情况呢？

那只能在LP上找了，LP也具有两部分，第一部分是LP的LS，LP的LS虽然满足小于X的条件，但是LP的LS中所有元素都是小于LP的，所以至少也是LP。

还有一部分，LP可能有左父母或者右父母，显然，右父母大于他的所有左子树，包括X，条件一都不满足，显然不行。左父母小于LP，所以它竞争不过LP。

所以最终结论就是，在只有左父母，没有左子树的情况，前驱 = 左父母的值。

那不存在左子树和左父母的情况呢？

那就只剩下右子树和右父母了，显然，右子树肯定不行，它的所有元素都大于X。那就只能在右父母中找了，毕竟虽然右父母大于它，但是右父母也有左/右父母和右子树。

右父母的右父母，和右子树都不行，都大于右父母本身，更大于X了。那就只能在右父母的左父母上找了，对于左父母来说，他的右子树全都大于他，即包括X的右父母和X，所以，此时找到的左父母就是我们的前驱。

所以，不存在左子树和左父母的情况，前驱 = 右父母的左父母（如果右父母不存在左父母，就一直往上遍历，直至出现左父母）。

分析完毕。下面是代码实现。

因为我们的二叉树的结点只有Left和Right指针，所以这题感觉要用递归来做，或者栈。下面我们用栈写一个吧（时间复杂度是O（N））

BinTree Predecessor(BinTree X,BinTree BST)
{
    if(X->Left!=NULL)
        return FindMax(X->Left);
    else
    {
        Stack S;
        S = CreatStack();
        while(BST!=X)
        {
            Push(S,BST);
            if(X->Data > BST->Data)
                BST = BST->Right;
            else if(X->Data < BST->Data)
                BST = BST->Left;
        }
        BinTree Par,Son;
        Son = X;
        while((Par = Pop(S))->Right!=Son)Son = Par;//相当于Case2&3结合，直至找到左母亲为止。
        return Par;
    }
}

 

插播一个递归和栈的区别：

接着分析后继：（类比前驱，如果前驱看懂了可以不用看，基本上是一样的分析思路）

满足两个条件，一是要大于当前键值，那么只有RP和RS区可以找。

                     二要求是其中最小的值。我们知道，对于RP来说，X、LS、RS都属于他的左子树，那么，X、LS和RS都是小于它的。

所以很显然，前驱就是RS中的最小值，即后继 = 右子树中的最小值。条件是：存在右子树。

那不存在右子树只有右父母的情况呢？

那只能在RP上找了，RP也具有两部分，第一部分是LP的RS，RP的RS虽然满足大于X的条件，但是RP的RS中所有元素都是大于LP的，所以找后继，至少也得是RP。

还有一部分，RP可能有左父母或者右父母，显然，左父母小于他的所有右子树，包括X，条件一都不满足，显然不行。右父母大于RP，所以它竞争不过RP。

所以最终结论就是，在只有右父母，没有右子树的情况，后继 = 右父母的值。

那不存在右子树和右父母的情况呢？

那就只剩下左子树和左父母了，显然，左子树肯定不行，它的所有元素都小于X。那就只能在左父母中找了，毕竟虽然左父母小于它，但是右父母也有它本身的左/右父母和左子树。

左父母的左父母，和左子树都不行，都小于左父母本身，更小于X了。那就只能在左父母的右父母上找了，对于它的右父母来说，他的左子树全都小于他，即包括X的左父母和X，所以，此时找到的右父母就是我们的后继。

所以，不存在右子树和右父母的情况，后继 = 左父母的右父母（如果左父母不存在右父母，就一直往上遍历，直至出现右父母）。

分析完毕。下面是代码实现，同样是用栈实现。

BinTree Successor(BinTree X,BinTree BST)
{
    if(X->Right)
        return FindMin(X->Right);
    else
    {
        Stack S;
        S = CreatStack();
        while(BST!=X)
        {
            Push(S,BST);
            if(X->Data > BST->Data)
                BST = BST->Right;
            else if(X->Data < BST->Data)
                BST = BST->Left;
        }
        BinTree Par,Son;
        Son = X;
        while((Par = Pop(S))->Left!=Son )Son = Par;
        return Par;
    }
}

基本上是一样的。