二叉树与链表

Posted 2023-04-22

参考技术A

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
方法一： 中序遍历将结果存到list中，然后根据list建立链表

方法二

给定一个二叉树， 原地 将它展开为一个单链表。

例如，给定二叉树

方法一：先序遍历存起来再改指向

方法二：迭代改变指向

方法三
发现遍历的顺序就是先序遍历，思考在先序遍历过程中将前一个遍历到的结点的右孩子指向当前结点，但是存在问题：前一个结点更改右指针后导致右子树丢失
替代方法：按照右、左、根的顺序遍历，将当前结点的右指针指向前一个遍历到的结点

方法四：迭代先序遍历

二叉树与链表之间的转换

目录

一、二叉树与双链表之间的转换

（1、解法一

（2、解法二

二、二叉树与单链表之间的转换 

 （1、解法一、前序遍历

（2、解法二、后序遍历

---

一、二叉树与双链表之间的转换

 牛客网链接：转换问题。

 

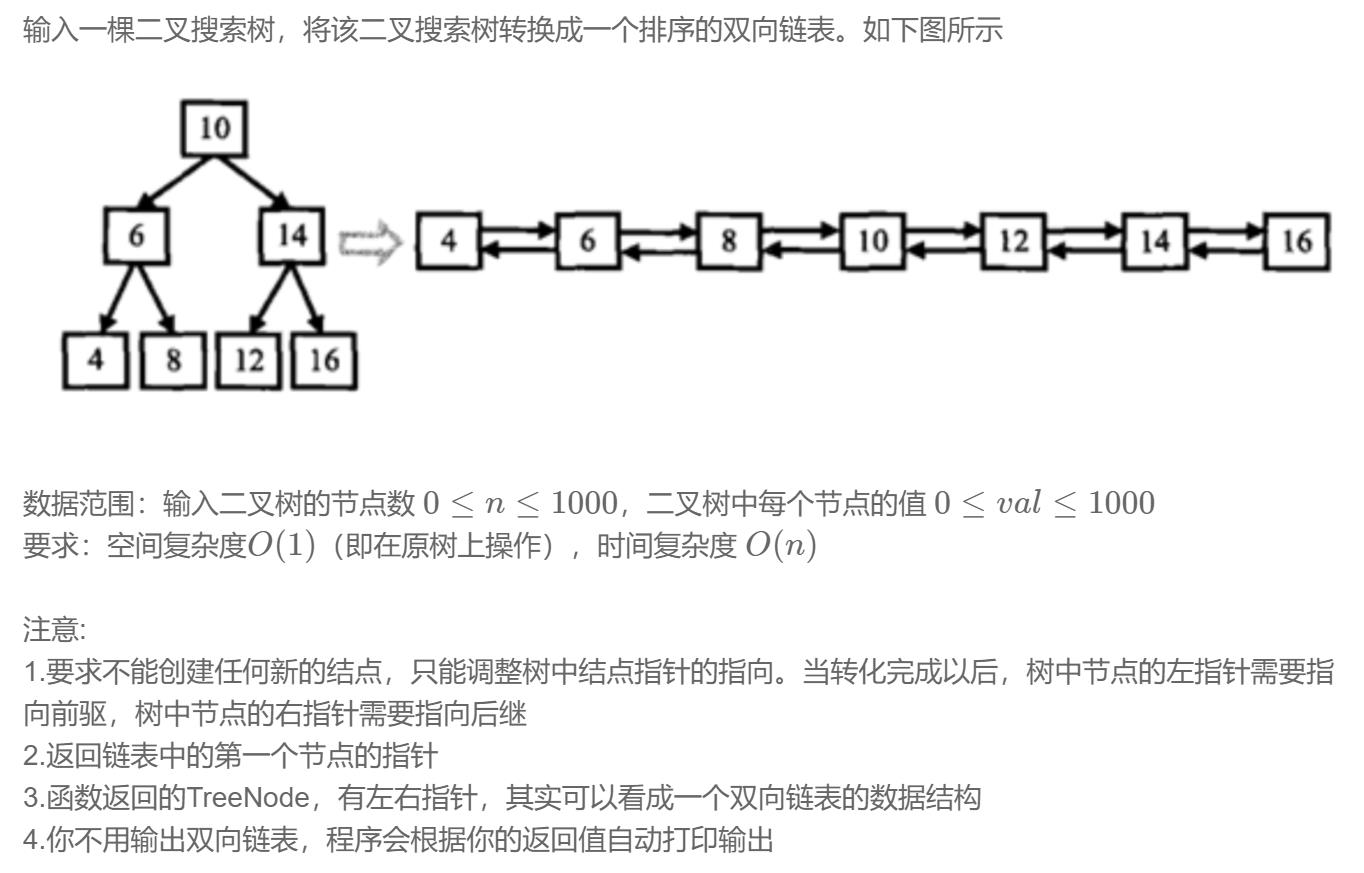
 对于这种链表转换的题目，都是要通过遍历来解决问题。

（1、解法一

我们可以专门定义一个函数来将双链表来进行转换，转换完成之后我们，转换完成之后我们找它的头节点就行了。

public class Solution {
    TreeNode cur=null;
    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree==null) return null;
        convertTree(pRootOfTree);
        
        TreeNode temp=pRootOfTree;
        while(temp.left!=null){
            temp=temp.left;
        }
        return temp;
    }
    public void convertTree(TreeNode pCur){
        if(pCur==null) return;
        convertTree(pCur.left);
        
        pCur.left=cur;
        if(cur!=null){
            cur.right=pCur;
        }
        cur=pCur;
        
        convertTree(pCur.right);
    }
}

（2、解法二

我们可以直接在本函数中进行遍历，我们定义两个变量，在函数内部进行定义。

public class Solution {
    TreeNode cur=null;
    TreeNode pre=null;
    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree==null) return null;
        
        Convert(pRootOfTree.left);
        
        if(cur==null){
            cur=pRootOfTree;
        }
        if(pre!=null){
            pRootOfTree.left=pre;
            pre.right=pRootOfTree;
        }
        pre=pRootOfTree;
        
        Convert(pRootOfTree.right);
        
        return cur;
    }
}

二、二叉树与单链表之间的转换 

力扣链接：题目。

 （1、解法一、前序遍历

class Solution {
    public void flatten(TreeNode root) {
        if(root==null) return;
        if(root.left!=null){
            TreeNode temp=root.left;
            while(temp.right!=null){
                temp=temp.right;
            }
            temp.right=root.right;
            root.right=root.left;
            root.left=null;
        }

        flatten(root.left);

        flatten(root.right);
    }
}

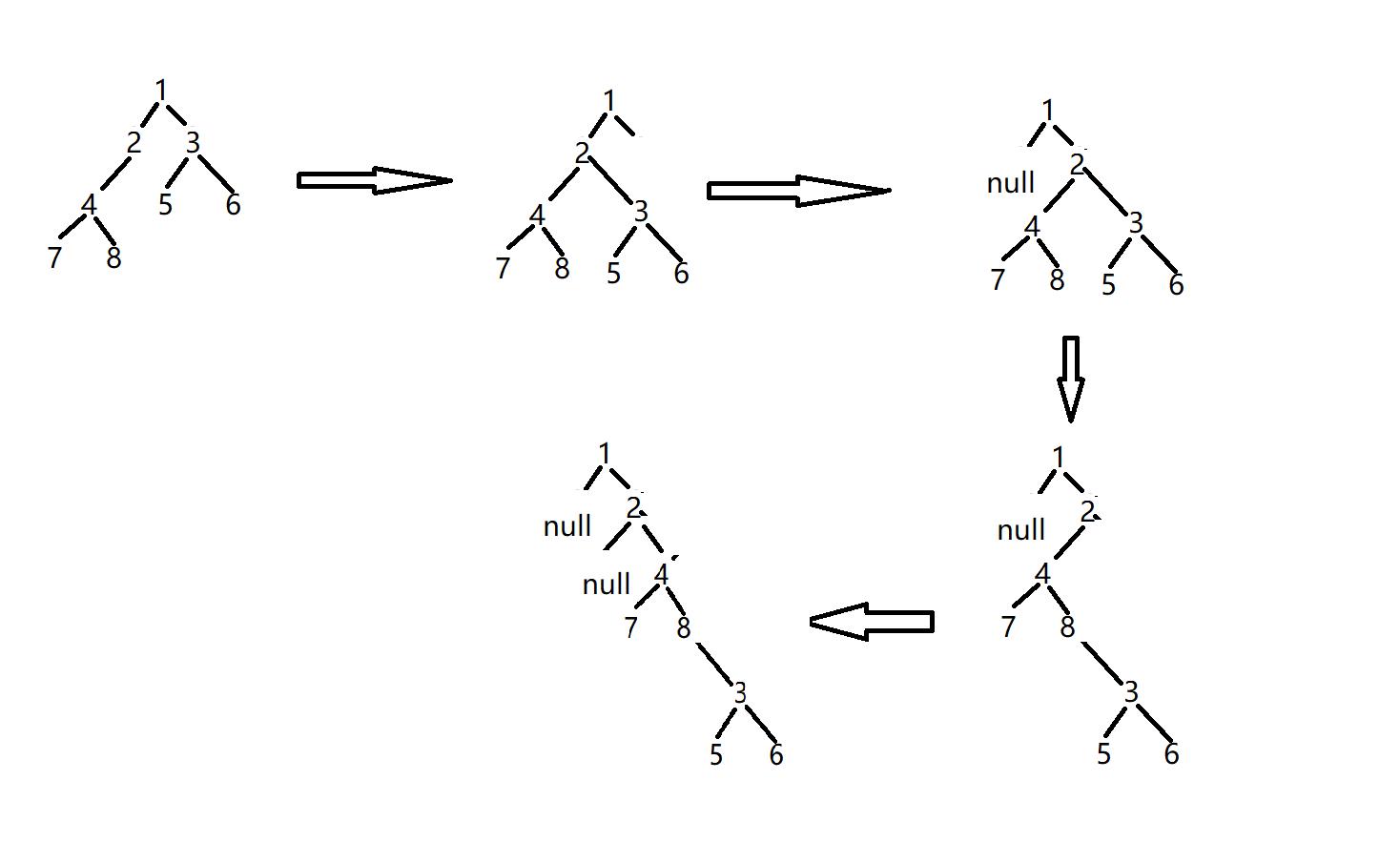
 对于前序遍历的方法，我们判断根节点的左子树是否为空，通过将右子树接到左子树的右结点上，再将左子树接到右子树上，把左子树置为空。用递归不断的遍历去做就行了。

（2、解法二、后序遍历

class Solution {
    public void flatten(TreeNode root) {
        if(root==null) return;
        flatten(root.left);
        flatten(root.right);

        TreeNode temp=root.right;
        root.right=root.left;
        root.left=null;

        while(root.right!=null){
            root=root.right;
        }
        root.right=temp;
    }
}

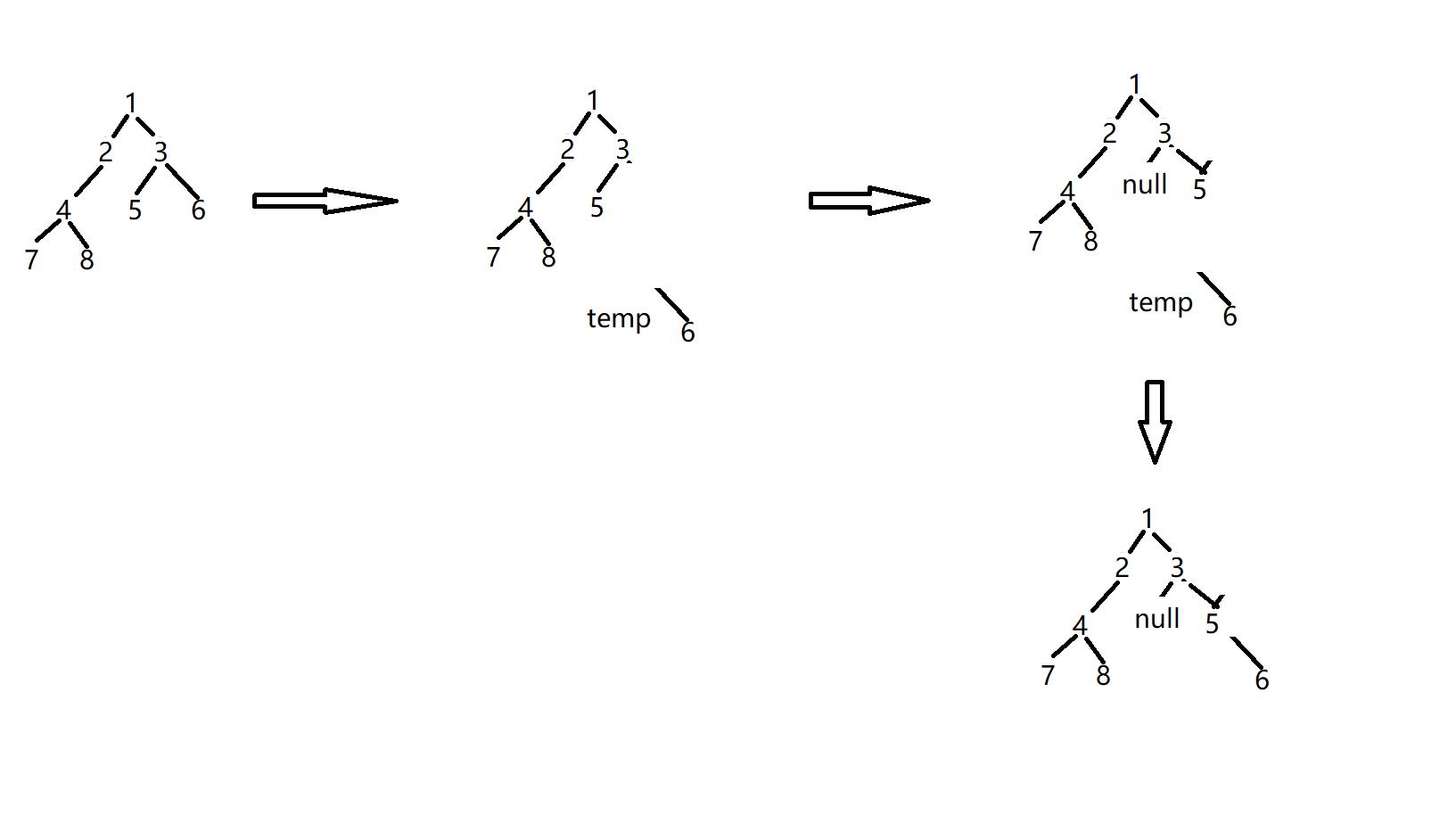
 我们通过后续遍历一步步还原，将右子树取出，将左子树转换成右子树，在将原来的右子树接入。不断的还原就行了。