noip 提高组 2010

Posted 2021-01-05 gtba

T1：机器翻译

题目背景

小晨的电脑上安装了一个机器翻译软件，他经常用这个软件来翻译英语文章。

题目描述

这个翻译软件的原理很简单，它只是从头到尾，依次将每个英文单词用对应的中文含义来替换。对于每个英文单词，软件会先在内存中查找这个单词的中文含义，如果内存中有，软件就会用它进行翻译；如果内存中没有，软件就会在外存中的词典内查找，查出单词的中文含义然后翻译，并将这个单词和译义放入内存，以备后续的查找和翻译。

假设内存中有$M$个单元，每单元能存放一个单词和译义。每当软件将一个新单词存入内存前，如果当前内存中已存入的单词数不超过$M-1$，软件会将新单词存入一个未使用的内存单元；若内存中已存入$M$个单词，软件会清空最早进入内存的那个单词，腾出单元来，存放新单词。

假设一篇英语文章的长度为$N$个单词。给定这篇待译文章，翻译软件需要去外存查找多少次词典？假设在翻译开始前，内存中没有任何单词。

输入输出格式

输入格式：

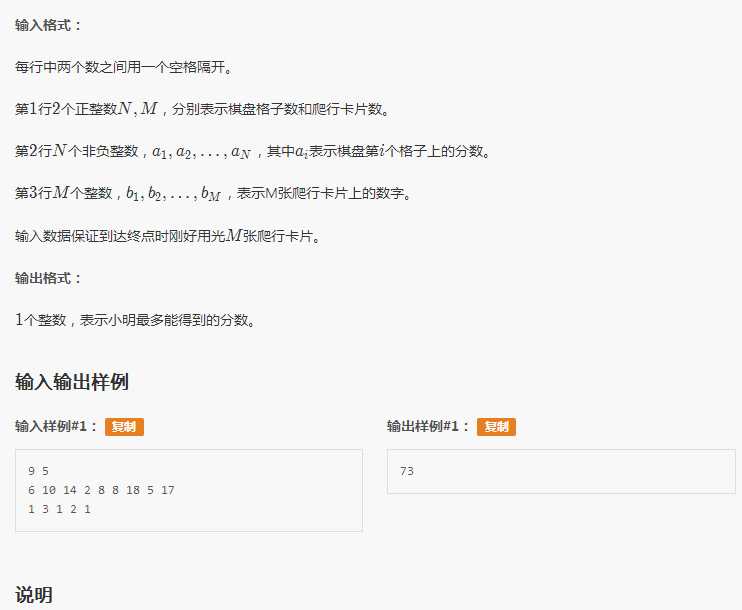
共$2$行。每行中两个数之间用一个空格隔开。

第一行为两个正整数$M,N$，代表内存容量和文章的长度。

第二行为$N$个非负整数，按照文章的顺序，每个数（大小不超过$1000$）代表一个英文单词。文章中两个单词是同一个单词，当且仅当它们对应的非负整数相同。

输出格式：

一个整数，为软件需要查词典的次数。

输入输出样例

输入样例#1： 复制

3 7
1 2 1 5 4 4 1

输出样例#1： 复制

5

 

 

说明

每个测试点$1s$

对于$10\%$的数据有$M=1,N\le 5$。

对于$100\%$的数据有$0\le M\le 100,0\le N\le 1000$。

整个查字典过程如下：每行表示一个单词的翻译，冒号前为本次翻译后的内存状况：

空：内存初始状态为空。

1．$1$：查找单词1并调入内存。

2． $12$：查找单词$2$并调入内存。

3． $12$：在内存中找到单词$1$。

4． $125$：查找单词$5$并调入内存。

5． $254$：查找单词$4$并调入内存替代单词$1$。

6．$254$：在内存中找到单词$4$。

7．$541$：查找单词1并调入内存替代单词$2$。

共计查了$5$次词典。

题解：

其实不难看出是个队列题，
当队列未满时，若这个单词在内存中没有，便直接放在队尾，并且将这个单词打上存在标记，表示这个单词在内存中有；
当队列已满且仍有单词在内存中没有出现，则踢出队首，将队首的存在标记删除，并将这个单词放入队列，打上存在标记。
每重复以上操作ans++；
若单词存在，那自然是继续操作喽。

代码：

 

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int n,m,x,ans,l,r,a[1005],b[1005];
int main() {
    cin>>m>>n;
    for(int i=1; i<=n; i++) {
        scanf("%d",&x);
        if(a[x]==0) {
            ans++,r++,b[r]=x,a[x]=1;
            if(r>m) l++,a[b[l]]=0;
        }
    }
    cout<<ans;
    return 0;
}

 

T2 乌龟棋

题解：

取或不取，很容易就想到是到DP题。
但会不会做，又是另一回事了。
看着看着题，突然想起来之前有做过一道题，和这道题很像。
之前考DP的时候考过，当时好像就我一个A了?
哎呀，切入主题。
开一个四维的数组，
ans[i][j][k][q]表示当1有i张，2有j张，3有k张，4有q张时的得分。
引入一个flag数组记录1~4的牌每种有几张。
用四重循环来遍历一下四种牌的所有可能。
当然题目中说了乌龟棋子自动获得起点格子的分数。
所以当1~4的牌都不用的时候，ans[0][0][0][0]为起点点数。
循环过程中定义一个get_power=i+j+k+q。
因为ans[i][j][k][q]就等于上一次尝试最大值加上这次到达的格子的点数。
于是ans[i][j][k][q]=max(ans[i][j][k][q],ans?+num[get_power])
慢慢你会发现，这个，，，不是个背包思想吗。
于是根据背包思想，你就可以很愉快地写代码了。
哦对了，要注意判断i,j,k,q不能等于0，因为我们在与上一层比较时难免会遇到i-1啊j-1什么的。，
最后输出ans[flag[1]][flag[2]][flag[3]][flag[4]]就好了

代码：

 

#include<iostream>
int ans[41][41][41][41],num[351],flag[5],n,m,x;
int main() {
    std::cin>>n>>m;
    std::cin>>num[1];
    ans[0][0][0][0]=num[1];
    for(int i=2; i<=n; i++)
        std::cin>>num[i];
    for(int i=1; i<=m; i++)
        std::cin>>x,flag[x]++;
    for(int i=0; i<=flag[1]; i++)
        for(int j=0; j<=flag[2]; j++)
            for(int k=0; k<=flag[3]; k++)
                for(int q=0; q<=flag[4]; q++) {
                    int get_power=1+i+j*2+k*3+q*4;
                    if(i!=0) ans[i][j][k][q]=std::max(ans[i][j][k][q],ans[i-1][j][k][q]+num[get_power]);
                    if(j!=0) ans[i][j][k][q]=std::max(ans[i][j][k][q],ans[i][j-1][k][q]+num[get_power]);
                    if(k!=0) ans[i][j][k][q]=std::max(ans[i][j][k][q],ans[i][j][k-1][q]+num[get_power]);
                    if(q!=0) ans[i][j][k][q]=std::max(ans[i][j][k][q],ans[i][j][k][q-1]+num[get_power]);
                }
    std::cout<<ans[flag[1]][flag[2]][flag[3]][flag[4]];
    return 0;
}

T3 关押罪犯

 

题解：

这里我用的并查集，出去学习的时候，老师们讲并查集时总会拿着个当例题。

于是在听过了几个老师巴拉巴拉地讲了好几遍后，埋头写这个题。

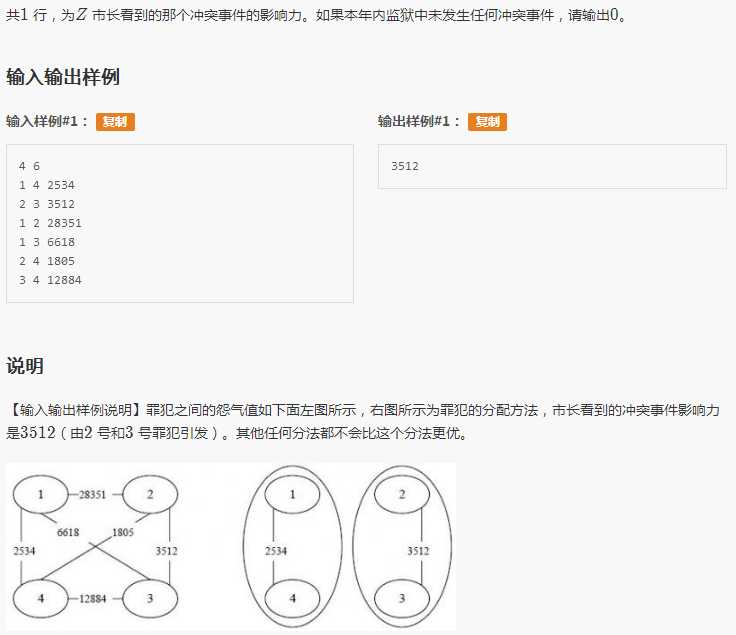
首先把所有冲突按照从大到小进行排序，然后进行操作。

检验，对于当前冲突的两个人是否能把他俩分开。

直到遇到两个人，他俩不可能被分开（如果分开了就跟前面冲突了），那他俩的冲突度就是最后的答案了。

利用并查集可以维护已知的一些人的关系。

代码：

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
struct node {
    int x,y,z;
} f[100005];
int n,m,a[20005],b[20005];
bool cmp(node a,node b) {
    return a.z>b.z;
}
int find(int x) {
    if(a[x]==x) return x;
    return a[x]=find(a[x]);
}
void ad(int x,int y) {
    a[find(a[x])]=find(a[y]);
}
bool check(int x,int y) {
    return find(x)==find(y)?1:0;
}
void add(int p,int mmp,int mml,int mmz) {
    f[p].x=mmp,f[p].y=mml,f[p].z=mmz;
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++) a[i]=i;
    for(int i=1,fa,fb,fc; i<=m; i++)
        scanf("%d%d%d",&fa,&fb,&fc),add(i,fa,fb,fc);
    sort(f+1,f+m+1,cmp);
    for(int i=1; i<=m+1; i++) {
        if(check(f[i].x,f[i].y)) {
            printf("%d",f[i].z);
            break;
        } else {
            if(!b[f[i].x]) b[f[i].x]=f[i].y;
            else ad(b[f[i].x],f[i].y);
            if(!b[f[i].y]) b[f[i].y]=f[i].x;
            else ad(b[f[i].y],f[i].x);
        }
    }
    return 0;
}

 

T4 引水入城

题解：

当初考DP时，这是第三题，得了八十分还是多少分来着。鬼知道我为什么会得一个这么鬼畜的分。

记忆化搜索，我最讨厌搜索了。

鬼知道我为什么对于搜索看到的第一眼就是不喜欢。

但是，迫不得已，毕竟，学习学习嘛。

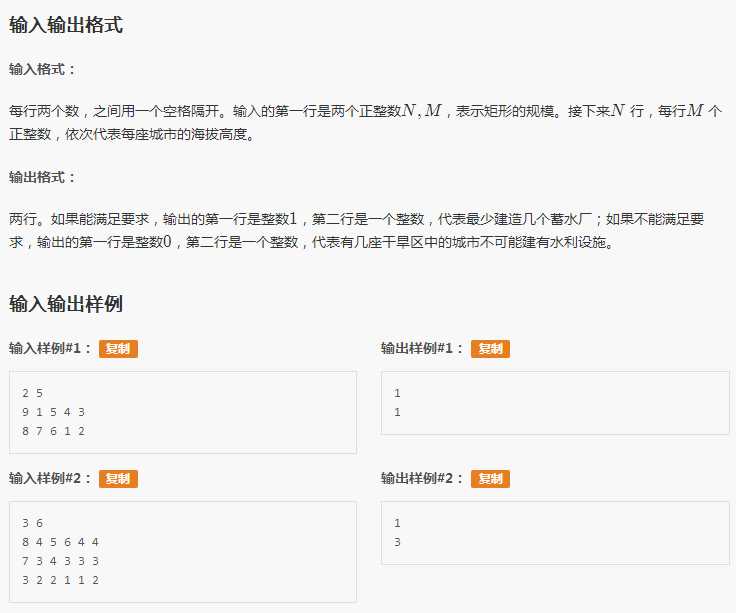
首先，第一问。

很好做，直接dfs或bfs求一下最下面一排的店有没有不能被覆盖到的就行了。

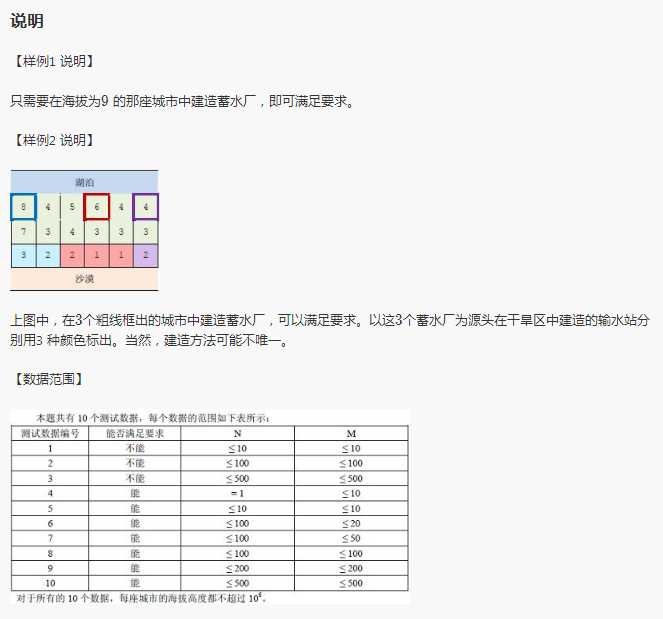
接下来第二问。

 

对第一排每个点进行dfs或bfs，搜出每个点能够覆盖到的区间，再做线段覆盖就行了。

代码：

 

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
struct node{
    int l,r;
}edge[101];
int n,m,map[501][501],f[501],cnt;
bool comp(node a,node b) {
    return a.l<b.l;
}
bool vis[501][501],ans[501];
void dfs(int x,int y,int tot) {
    vis[x][y]=1;
    if(x==m) {
        ans[y]=1;
        edge[tot].l=min(edge[tot].l,y);
        edge[tot].r=max(edge[tot].r,y);
    }
    if(map[x+1][y]<map[x][y]&&x!=m&&!vis[x+1][y]) dfs(x+1,y,tot);
    if(map[x-1][y]<map[x][y]&&x!=1&&!vis[x-1][y]) dfs(x-1,y,tot);
    if(map[x][y+1]<map[x][y]&&y!=n&&!vis[x][y+1]) dfs(x,y+1,tot);
    if(map[x][y-1]<map[x][y]&&y!=1&&!vis[x][y-1]) dfs(x,y-1,tot);
}
int main() {
    cin>>m>>n;
    for(int i=1; i<=n; ++i) edge[i].l=f[i]=0x7fffffff;
    for(int i=1; i<=m; ++i)
        for(int j=1; j<=n; ++j)
            cin>>map[i][j];
    for(int i=1; i<=n; ++i) {
        memset(vis,0,sizeof(vis));
        dfs(1,i,i);
    }
    for(int i=1; i<=n; ++i)
        if(!ans[i]) ++cnt;
    if(cnt) printf("0
%d
",cnt);
    else {
        puts("1");
        for(int i=1; i<=n; ++i)
            for(int j=1; j<=n; ++j)
                if(i>=edge[j].l&&i<=edge[j].r)
                    f[i]=min(f[i],f[edge[j].l-1]+1);
        printf("%d
",f[n]);
    }
    return 0;
}

 

一世安宁