一些说明
我将会写一系列关于算法的博客,因为我是程序员,并不是计算机科学家,也即我是搞工程的,并不是搞学术的,所以对于我来说,最重要的就是
1.有哪些算法
2.这些算法的原理
3.这些算法的实现
4.这些算法的效率
而其他的,相对而言,并没有那么重要,比如算法的证明,所以以后的博客都会按照上述的思维撰写。
一、首先定义一个抽象类,里面集成了排序算法所需要的共同的方法:
public abstract class SortBase { public abstract Integer[] sort(Integer[] a); public static void print(Integer[] arrayForSort) { System.out.print("["); for(int i=0;i<arrayForSort.length;i++) { if(i == arrayForSort.length - 1) { System.out.print(arrayForSort[i]); } else { System.out.print(arrayForSort[i] + " ,"); } } System.out.println("]"); } public static void print(String prefix,Integer[] arrayForSort) { System.out.print(prefix + ": "); System.out.print("["); for(int i=0;i<arrayForSort.length;i++) { if(i == arrayForSort.length - 1) { System.out.print(arrayForSort[i]); } else { System.out.print(arrayForSort[i] + " ,"); } } System.out.println("]"); } }
二、选择排序:
选择排序可以说是最简单的一种排序方法:
1.找到数组中最小的那个元素
2.将最小的这个元素和数组中第一个元素交换位置
3.在剩下的元素中找到最小的的元素,与数组第二个元素交换位置
重复以上步骤,即可以得到有序数组。
代码如下:
public class SelectionSort extends SortBase { public Integer[] sort(Integer[] a) { print("init",a); Integer minIndex = 0; Integer temp = 0; for(int i=0;i<a.length;i++) { minIndex = i; for(int j=i+1;j<a.length;j++) { if(a[j] < a[minIndex]) { minIndex = j; } } temp = a[i]; a[i] = a[minIndex]; a[minIndex] = temp; print((i+1) + "",a); } return a; } public static void main(String[] args) { Integer[] a = {2,1,5,9,0,6,8,7,3}; print("result",(new SelectionSort()).sort(a)); } }
我在代码中打出了每次排序的结果,运行结果如下:
init: [2 ,1 ,5 ,9 ,0 ,6 ,8 ,7 ,3] 1: [0 ,1 ,5 ,9 ,2 ,6 ,8 ,7 ,3] 2: [0 ,1 ,5 ,9 ,2 ,6 ,8 ,7 ,3] 3: [0 ,1 ,2 ,9 ,5 ,6 ,8 ,7 ,3] 4: [0 ,1 ,2 ,3 ,5 ,6 ,8 ,7 ,9] 5: [0 ,1 ,2 ,3 ,5 ,6 ,8 ,7 ,9] 6: [0 ,1 ,2 ,3 ,5 ,6 ,8 ,7 ,9] 7: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9] 8: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9] 9: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9] result: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9]
效率:对于长度为N的数组,选择排序需要大约N²/2次比较和N次交换。也即最好、最差、平均时间效率均为O(n²),只需要一个辅助变量帮助交换元素。
选择排序可以看成是冒泡排序的扩展,一个是把最小或最大的选出来,再交换,一个是一直交换直到最大最小的出现在正确的位置上,选择排序相对于冒泡排序,比较次数是一样的,但是交换次数要少很多。
三、插入排序:
插入排序类似整理扑克牌,将每一张牌插到其他已经有序的牌中适当的位置。
插入排序由N-1趟排序组成,对于P=1到N-1趟,插入排序保证从位置0到位置P上的元素为已排序状态。
简单的说,就是插入排序总共需要排序N-1趟,从index为1开始,讲该位置上的元素与之前的元素比较,放入合适的位置,这样循环下来之后,即为有序数组。
代码实现:
public class InsertionSort extends SortBase { @Override public Integer[] sort(Integer[] a) { // TODO Auto-generated method stub print("init",a); Integer temp = 0; for(int i=1;i<a.length;i++) { //只能从当前索引往前循环,因为索引前的数组皆为有序的,索引只要确定当前索引的数据的为止即可 for(int j=i;j>0 && a[j] < a[j-1];j--) { temp = a[j]; a[j] = a[j-1]; a[j-1] = temp; } print(i +"",a); } print("result",a); return a; } public static void main(String[] args) { Integer[] a = {2,1,5,9,0,6,8,7,3}; (new InsertionSort()).sort(a); } }
运行结果:
init: [2 ,1 ,5 ,9 ,0 ,6 ,8 ,7 ,3] 1: [1 ,2 ,5 ,9 ,0 ,6 ,8 ,7 ,3] 2: [1 ,2 ,5 ,9 ,0 ,6 ,8 ,7 ,3] 3: [1 ,2 ,5 ,9 ,0 ,6 ,8 ,7 ,3] 4: [0 ,1 ,2 ,5 ,9 ,6 ,8 ,7 ,3] 5: [0 ,1 ,2 ,5 ,6 ,9 ,8 ,7 ,3] 6: [0 ,1 ,2 ,5 ,6 ,8 ,9 ,7 ,3] 7: [0 ,1 ,2 ,5 ,6 ,7 ,8 ,9 ,3] 8: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9] result: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9]
效率:如果目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1)次。平均来说插入排序算法的时间复杂度为O(n^2)
四、希尔排序
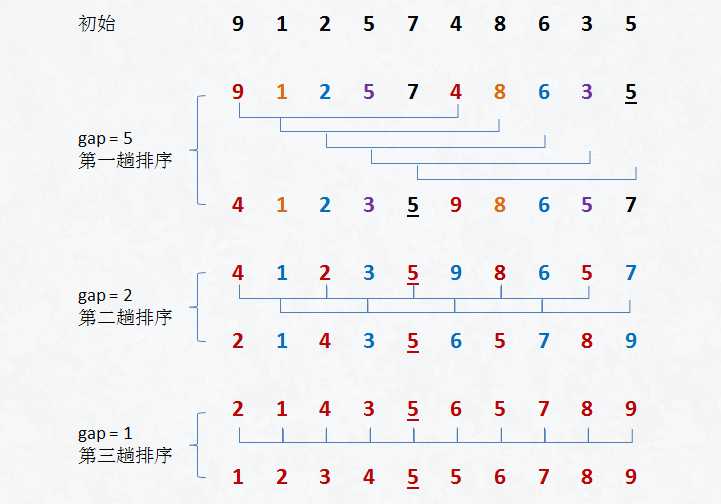
把记录按步长 gap 分组,对每组记录采用直接插入排序方法进行排序。
随着步长逐渐减小,所分成的组包含的记录越来越多,当步长的值减小到 1 时,整个数据合成为一组,构成一组有序记录,则完成排序。
实现代码:
public class ShellSort extends SortBase { @Override public Integer[] sort(Integer[] a) { // TODO Auto-generated method stub print("init",a); Integer h = a.length; Integer temp = 0; while(h >= 1) { for(int i=h;i<a.length;i++) { for(int j=i;j>=h && a[j] < a[j-h];j -= h) { temp = a[j]; a[j] = a[j-h]; a[j-h] = temp; } } h /= 9; } print("result",a); return a; } public static void main(String[] args) { Integer[] a = {2,1,5,9,0,6,8,7,3}; (new ShellSort()).sort(a); } }
运行结果:
init: [2 ,1 ,5 ,9 ,0 ,6 ,8 ,7 ,3] 1: [0 ,1 ,5 ,7 ,2 ,6 ,8 ,9 ,3] 2: [0 ,1 ,2 ,6 ,3 ,7 ,5 ,9 ,8] 3: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9] result: [0 ,1 ,2 ,3 ,5 ,6 ,7 ,8 ,9]
效率:
最坏情况时间复杂度为:O(n^1.5),平均时间复杂度为O(nlogn)。
