SPOJ - TSUM 母函数+FFT+容斥

Posted 2021-01-04 suut

题意：n个数，任取三个加起来，问每个可能的结果的方案数。

题解:构造母函数ABC,比如现在有 1 2 3 三个数。则

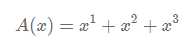
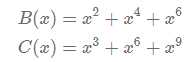
其中B表示同一个数加两次，C表示用三次。然后考虑去重。

A^3表示可重复地拿三个。（无顺序）

然后我们去掉拿了两个相同的方案A*B，由于有三种顺序（xxy,xyx,yxx) 所以*3

最后再加上多减了的 拿三个相同的的方案C，一共减了三次，多减了两次所以*2

最后除以3*2*1去掉顺序

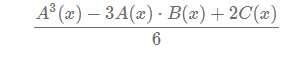
然后fft即可

坑：数据有负数，所以读入需要+2e4预处理trk，最后减去6e4,因为每一项都是三次方,显然这样可以得到正确结果

 

#include <cstdio>
#include <cmath>
#include <complex>
#include <algorithm>
#include <iostream>
using namespace std; 
typedef std::complex<double> complex_t;
const int badass=6e4;  
const int MaxL = 18, MaxN = 1 << MaxL;
typedef complex<double> complex_t;
complex_t A[MaxN], B[MaxN], C[MaxN];
complex_t eps[MaxN], inv_eps[MaxN];
void init_eps(int p)
{
    double pi = acos(-1);
    //double angle = 2.0 * pi / p;
    for (int i = 0; i != p; ++i)
        eps[i] = complex_t(cos(2.0 * pi * i / p), sin(2.0 * pi * i / p));
    for (int i = 0; i != p; ++i)
        inv_eps[i] = conj(eps[i]);
}



void transform(int n, complex_t *x, complex_t *w)
{
    for (int i = 0, j = 0; i != n; ++i)
    {
        if (i > j) std::swap(x[i], x[j]);
        for (int l = n >> 1; (j ^= l) < l; l >>= 1);
    }

    for (int i = 2; i <= n; i <<= 1)
    {
        int m = i >> 1;
        for (int j = 0; j < n; j += i)
        {
            for (int k = 0; k != m; ++k)
            {
                complex_t z = x[j + m + k] * w[n / i * k];
                x[j + m + k] = x[j + k] - z;
                x[j + k] += z;
            }
        }
    }
}



int main()
{
    
    int n, max_v = 0;
    std::scanf("%d", &n);
    for (int i = 0; i != n; ++i)
    {
        int v;
        std::scanf("%d", &v);v+=2e4; 
        A[v] += 1.0;
        B[v * 2] += 1.0;
        C[v * 3] += 1.0;
        if (v * 3 > max_v) max_v = v * 3;
    }

    int m = 1;
    while (m < max_v) m <<= 1;//m<<=1; 
    init_eps(m);
    transform(m, A, eps);
    transform(m, B, eps);
    for (int i = 0; i != m; ++i)
        A[i] = A[i] * A[i] * A[i] / 6.0 - A[i] *B[i]  / 2.0 ;
    transform(m, A, inv_eps);
    for (int i = 0; i != m; ++i)
        A[i] = A[i] / double(m) + C[i] / 3.0;
    for (int i = 0; i != m; ++i)
    {
        int x = int(A[i].real() + 0.5);
        if (x) std::printf("%d : %d
", i-badass, x);
    }
    return 0;
}
/*
5
-1
2
3
0
5
*/